vẽ hình giúp mình ạ

Những câu hỏi liên quan

Giúp mình với ạ (bài hình vẽ hình giúp mình ạ)
\(3x=4z\Rightarrow\dfrac{x}{4}=\dfrac{z}{3}\); \(\dfrac{x}{5}=\dfrac{y}{6}\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{z}{15}=\dfrac{y}{24}\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{z}{15}=\dfrac{y}{24}=\dfrac{x-y+z}{20-24+15}=\dfrac{121}{11}=11\)
\(\Rightarrow x=20.11=220;z=15.11=165;y=264\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
vẽ giúp mình hình này (phải có 3 hình) trên giấy 4 ô li ạ. kể giúp mình thông số luôn. mình cảm ơn ạ, cần gấp.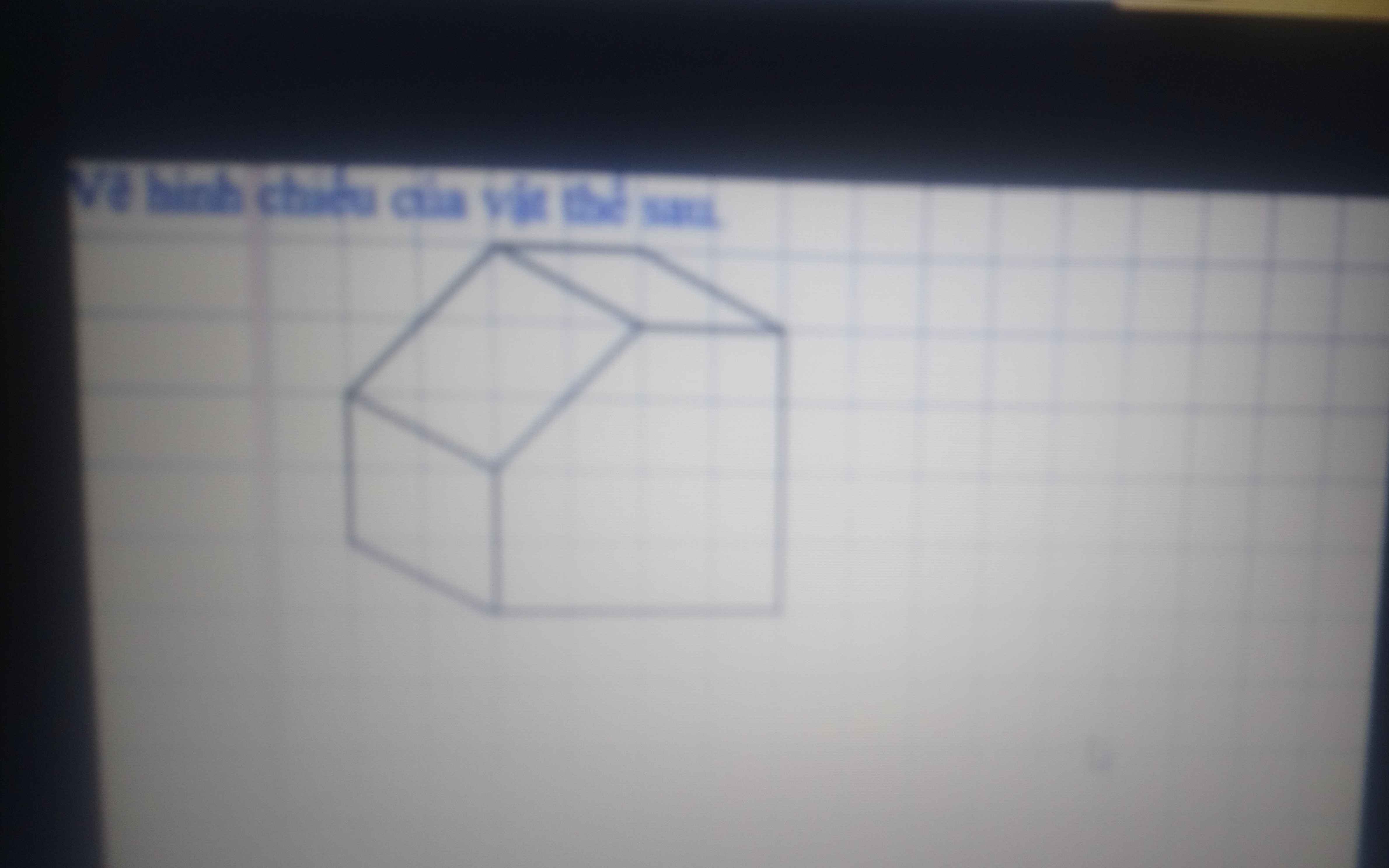

Làm hết giúp mình với các bạn trình bày vẽ hình giúp mình với ạ gấp lắm ạ
Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)
Đúng 0
Bình luận (0)
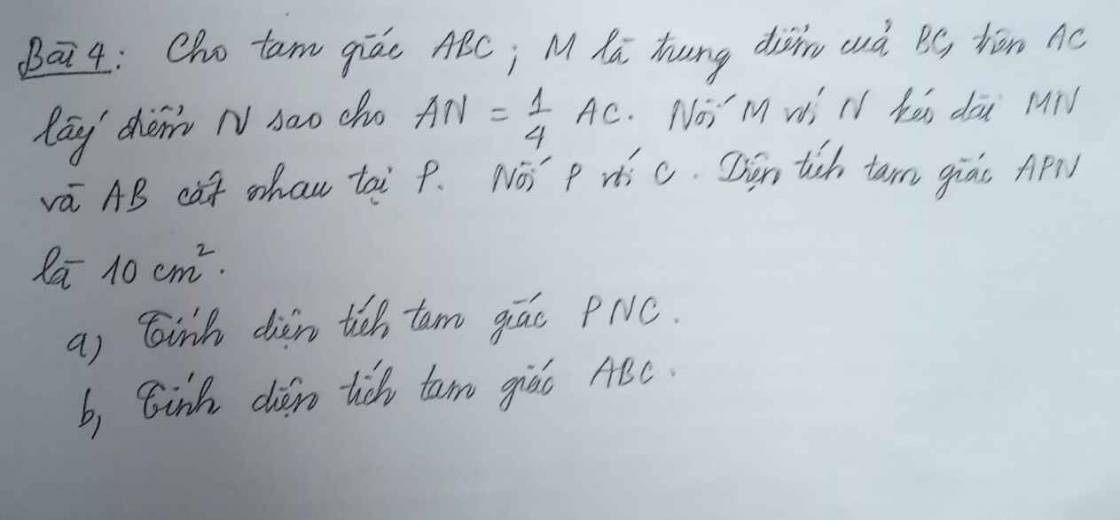
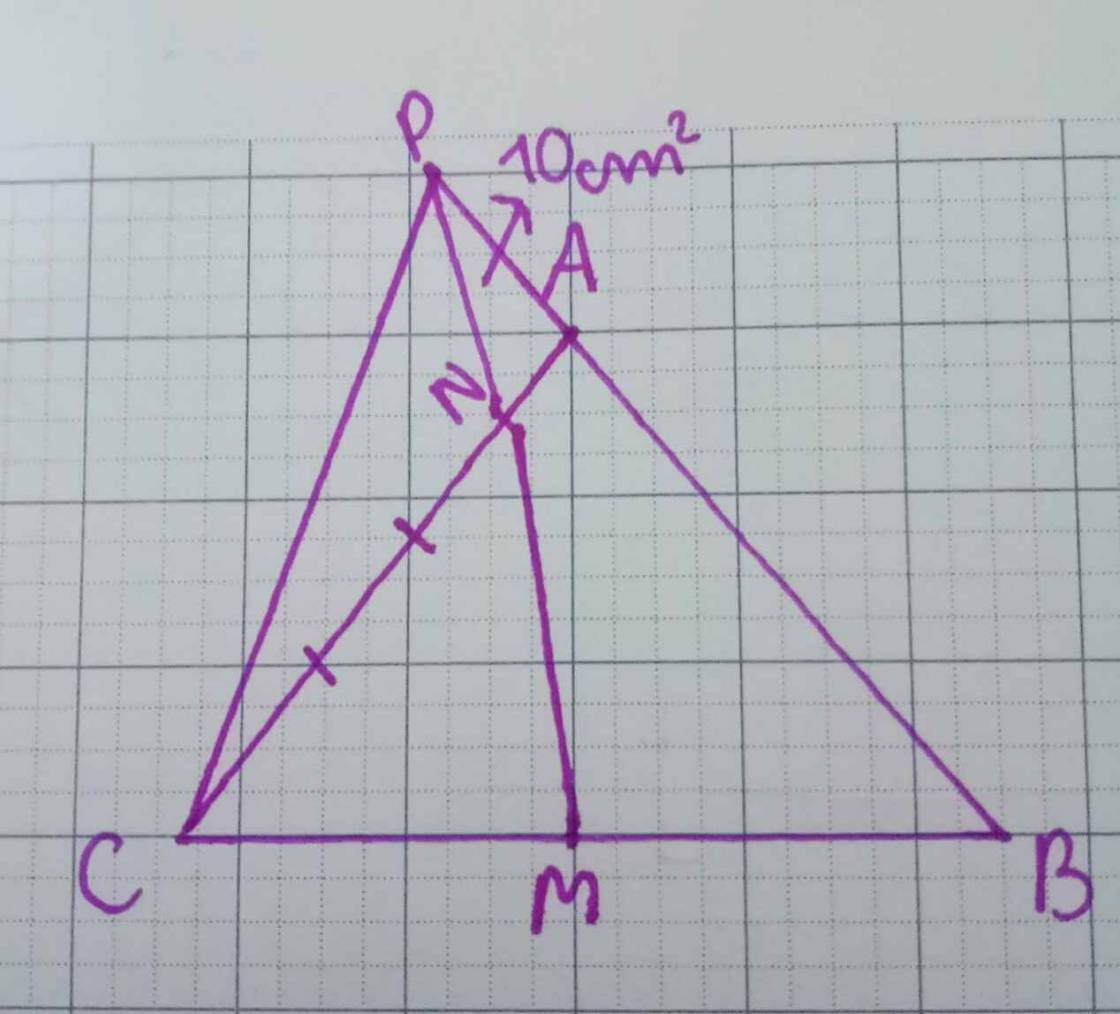 Giúp mình với ạ! Hình mình vẽ rồi.
Giúp mình với ạ! Hình mình vẽ rồi.
Giúp mình với ạ, mình cảm ơn!(vẽ hình)
Đọc tiếp
Giúp mình với ạ, mình cảm ơn!(vẽ hình)
Giải giúp mình bài 4 tự luận với ạ , vẽ hình giúp mình nha
4:
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
góc BAC=90 độ
=>ABDC là hcn
=>ΔACD vuông tại C
b: Xét ΔKAB vuông tại A và ΔKCD vuông tại C có
KA=KC
AB=CD
=>ΔKAB=ΔKCD
=>KB=KD
c: Xét ΔACD có
DK,CM là trung tuyến
DK cắt CM tại I
=>I là trọng tâm
=>KI=1/3KD
Xét ΔCAB có
AM,BK là trung tuyến
AM cắt BK tại N
=>N là trọng tâm
=>KN=1/3KB=KI
Đúng 0
Bình luận (0)
các bạn giúp mình giải với ạ, ko cần vẽ hình đâu ạ, mình cảm ơn 
b: Xét ΔMNP vuông tại M có MH là đường cao
nên \(NH\cdot NP=MN^2\left(1\right)\)
Xét ΔMNK vuông tại M có MQ là đường cao
nên \(NQ\cdot NK=MN^2\left(2\right)\)
Từ (1) và (2) suy ra \(NH\cdot NP=NQ\cdot NK\)
Đúng 0
Bình luận (0)
Mình cần 1 bài vẽ lọ , hoa và quả - vẽ hình , ai giúp mình hk ạ
GIÚP MÌNH NHANH ĐẦY ĐỦ VẼ HÌNH MÌNH CẢM ƠN Ạ
Giải:
a) Vì +) Oy;Oz cùng ∈ 1 nửa mặt phẳng bờ chứa tia Ox
+) \(x\widehat{O}y< x\widehat{O}z\left(30^o< 150^o\right)\)
⇒Oy nằm giữa Ox và Oz
\(\Rightarrow x\widehat{O}y+y\widehat{O}z=x\widehat{O}z\)
\(30^o+y\widehat{O}z=150^o\)
\(y\widehat{O}z=150^o-30^o\)
\(y\widehat{O}z=120^o\)
b) Vì Ot là tia p/g của \(y\widehat{O}z\)
\(\Rightarrow y\widehat{O}t=t\widehat{O}z=\dfrac{y\widehat{O}z}{2}=\dfrac{120^o}{2}=60^o\)
c) Vì Om là tia đối của Oy
\(\Rightarrow y\widehat{O}m=180^o\)
\(\Rightarrow x\widehat{O}y+y\widehat{O}m=180^o\) (2 góc kề bù)
\(30^o+y\widehat{O}m=180^o\)
\(y\widehat{O}m=180^o-30^o\)
\(y\widehat{O}m=150^o\)
Vì On là tia đối của Ox
\(\Rightarrow x\widehat{O}n=180^o\)
\(\Rightarrow x\widehat{O}m+m\widehat{O}n=180^o\) (2 góc kề bù)
\(150^o+m\widehat{O}n=180^o\)
\(m\widehat{O}n=180^o-150^o\)
\(m\widehat{O}n=30^o\)
\(\Rightarrow x\widehat{O}z+z\widehat{O}n=180^o\) (2 góc kề bù)
\(150^o+z\widehat{O}n=180^o\)
\(z\widehat{O}n=180^o-150^o\)
\(z\widehat{O}n=30^o\)
\(\Rightarrow z\widehat{O}n+n\widehat{O}m=z\widehat{O}m\)
\(30^o+30^o=z\widehat{O}m\)
\(\Rightarrow z\widehat{O}m=60^o\)
Vì +) \(z\widehat{O}n+n\widehat{O}m=z\widehat{O}m\)
+) \(z\widehat{O}n=n\widehat{O}m=60^o\)
⇒On là tia p/g của \(z\widehat{O}m\)
Chúc bạn học tốt!
Đúng 0
Bình luận (0)




















