\(3x=4z\Rightarrow\dfrac{x}{4}=\dfrac{z}{3}\); \(\dfrac{x}{5}=\dfrac{y}{6}\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{z}{15}=\dfrac{y}{24}\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{z}{15}=\dfrac{y}{24}=\dfrac{x-y+z}{20-24+15}=\dfrac{121}{11}=11\)
\(\Rightarrow x=20.11=220;z=15.11=165;y=264\)
Bài 2:
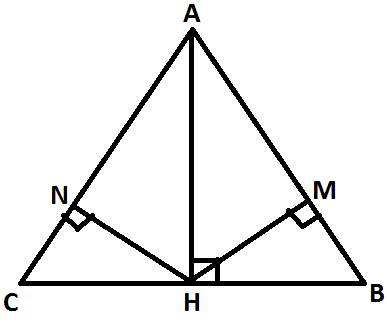
a: Xét ΔBAC có \(\dfrac{BM}{BA}=\dfrac{BN}{BC}\)
nên MN//AC
b: Ta có: BM+MA=BA
BN+NC=BC
mà BM=BN
và BA=BC
nên MA=NC
Xét ΔMAC và ΔNCA có
MA=NC
\(\widehat{MAC}=\widehat{NCA}\)
AC chung
Do đó: ΔMAC=ΔNCA
=>\(\widehat{MCA}=\widehat{NAC}\)
=>\(\widehat{IAC}=\widehat{ICA}\)
=>ΔIAC cân tại I
=>IA=IC
=>I nằm trên đường trung trực của AC(1)
ta có: BA=BC
=>B nằm trên đường trung trực của AC(2)
Từ (1) và (2) suy ra BI là đường trung trực của AC
=>BI\(\perp\)AC
mà MN//AC
nên BI\(\perp\)MN
















 Vẽ hình giúp mình với,mình cần gấp.
Vẽ hình giúp mình với,mình cần gấp.