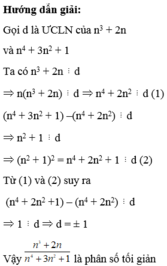Chứng minh rằng: 7.n+10/5.n+9 là phân số tối giản với mọi số nguyên n.

Những câu hỏi liên quan
chứng minh rằng n+6/n+7 là phân số tối giản với mọi số nguyên
Muốn chứng minh \(\frac{n+6}{n+7}\)là phân số tối giản thì cần phải chứng minh n + 6 và n + 7 nguyên tố cùng nhau hay ƯCLL của chúng bằng 1.
Gọi d là ƯCLL của n + 6 và n + 7 (d>0)
\(\Rightarrow n+6⋮d\) và \(n+7⋮d\)
\(\Rightarrow\left(n+7\right)-\left(n+6\right)⋮d\)(hai số chia hết cho d nên hiệu của nó cũng chia hết cho d)
\(\Rightarrow1⋮d\)\(\Rightarrow d=1\)(vì d>0)
=> n + 6 và n + 7 nguyên tố cùng nhau
Vậy \(\frac{n+6}{n+7}\)là phân số tối giản.
Đúng 1
Bình luận (0)
Có: n+6 và n+7 là 2 số nguyên liên tiếp nên: hoặc n+6 chẵn thì n+7 lẻ hoặc n+6 lẻ thì n+7 chẵn
Vì thế: ƯCLN(n+6;n+7)=1 hay n+6/n+7 là phân số tối giản
Đúng 0
Bình luận (1)
Bài 1 : Chứng tỏ rằng với mọi số nguyên n, phân số \(\frac{3n-5}{3-2n}\)là phân số tối giản.
Bài 2 : Cho n \(\in\)N*. Biết n - 10, n+10, n+ 60 đều là các số nguyên tố. Chứng minh rằng n + 90 cũng là số nguyên tố.
Gọi (n^3+2n ; n^4+3n^2+1) là d => n^3+2n chia hết cho d và n^4+3n^2+1 chia hết cho d. =>n(n^3+2n) chia hết cho d hay n^4+2n^2 chia hết cho d. do đó (n^4+3n^2+1) - (n^4+2n^2) chia hết chod hay n^2 +1 chia hết cho d (1). => (n^2+1)(n^2+1) chia hết cho d hay n^4+2n^2+1 chia hết cho d. => (n^4+3n^2+1) ...
Đúng 0
Bình luận (0)
Bài 1 :
Ta có :
\(\frac{3n-5}{3-2n}=\frac{3n-5}{-\left(2n-3\right)}\)
Gọi \(ƯCLN\left(3n-5;3-2n\right)=d\)
\(\Rightarrow\)\(\hept{\begin{cases}3n-5⋮d\\-\left(2n-3\right)⋮d\end{cases}\Rightarrow\hept{\begin{cases}2\left(3n-5\right)⋮d\\-3\left(2n-3\right)⋮d\end{cases}\Rightarrow}\hept{\begin{cases}6n-10⋮d\\-6n+9⋮d\end{cases}}}\)
\(\Rightarrow\)\(\left(6n-10\right)+\left(-6n+9\right)⋮d\)
\(\Rightarrow\)\(\left(6n-6n\right)\left(-10+9\right)⋮d\)
\(\Rightarrow\)\(\left(-1\right)⋮d\)
\(\Rightarrow\)\(d\inƯ\left(1\right)\)
Mà \(Ư\left(1\right)=\left\{1;-1\right\}\)
\(\Rightarrow\)\(ƯCLN\left(3n-5;3-2n\right)=\left\{1;-1\right\}\)
Vậy \(\frac{3n-5}{3-2n}\) là phân số tối giản với mọi số nguyên n
Chúc bạn học tốt ~
Đúng 0
Bình luận (0)
chứng minh rằng n+1 phần n+2 là phân số tối giản với mọi số nguyên n
Gọi d=ƯCLN(n+1;n+2)
=>n+1-n-2 chia hết cho d
=>-1 chia hết cho d
=>d=1
=>PSTG
Đúng 1
Bình luận (1)
1. Chứng minh rằng n-5/3n-14 là phân số tối giản với mọi số nguyên n.
2. Tìm số nguyên n để phân số 2n-1/3n+2 rút gọn được
Gọi ước chung lớn nhất của n - 5 và 3n - 14 là d, ta có
3 ( n - 5) - ( 3n - 14)= -1 chia hết cho d
=> d = -1 hoặc 1, do đó n - 5 và 3n - 14 là nguyên tố cùng nhau
vậy n - 5/3n - 14 là phân số tối giản
Đúng 0
Bình luận (0)
Chứng minh rằng với mọi số nguyên n thì phân số n 3 + 2 n n 4 + 3 n 2 + 1 là phân số tối giản
chứng minh rằng với mọi số nguyên n thì phân số 7n+1/6n+1 là phân số tối giản
Gọi d=ƯCLN(7n+1;6n+1)
=>42n+6-42n-7 chia hết cho d
=>1 chia hết cho d
=>d=1
=>PSTG
Đúng 0
Bình luận (0)
Chứng minh rằng với mọi số nguyên n thì phân số P= 2n + 3/4n + 8 là phân số tối giản
Gọi d=ƯCLN(2n+3;4n+8)
=>\(\left\{{}\begin{matrix}4n+8⋮d\\2n+3⋮d\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4n+8⋮d\\4n+6⋮d\end{matrix}\right.\Leftrightarrow4n+8-4n-6⋮d\)
=>\(2⋮d\)
mà 2n+3 lẻ
nên d=1
=>ƯCLN(2n+3;4n+8)=1
=>\(P=\dfrac{2n+3}{4n+8}\) là phân số tối giản với mọi n<>-2
Đúng 0
Bình luận (0)
Chứng minh rằng với mọi n là số nguyên thì phân số nguyên 7n+8 phần 5n+3 là phân số tối giản
n=0 nhé
Trình bày ra đi
gọi ƯCLN của 7n+8 và 5n+3 là d
ta có 7n+8 chia hết cho d=>35n+40 chia hết cho d
5n+3 chia hết cho d=>35n+21 chia hết cho d
=>(35n+40)-(35n+21) chia hết cho d
hay 17 chia hết cho d
vì 17 là số nguyên tố nên 7n+8/5n+3 là phân số tối giản.
nha ^.^
FrogDJ
a, Chứng minh rằng với mọi số tự nhiên n thì \(\dfrac{n+1}{2n+3}\) là phân số tối giản
b, Chứng minh rằng với mọi số tự nhiên a, b thì \(\dfrac{7a+5b}{9a+4b}\) là phân số tối giản
a/
Gọi $d=ƯCLN(n+1, 2n+3)$
$\Rightarrow n+1\vdots d; 2n+3\vdots d$
$\Rightarrow 2n+3-2(n+1)\vdots d$
$\Rightarrow 1\vdots d$
$\Rightarrow d=1$
Vậy $\frac{n+1}{2n+3}$ là phân số tối giản với mọi số tự nhiên $n$
Đúng 0
Bình luận (0)
b/
Cho $a=2, b=2$ thì phân số đã cho bằng $\frac{24}{26}$ không là phân số tối giản bạn nhé.
Bạn xem lại đề.
Đúng 0
Bình luận (0)