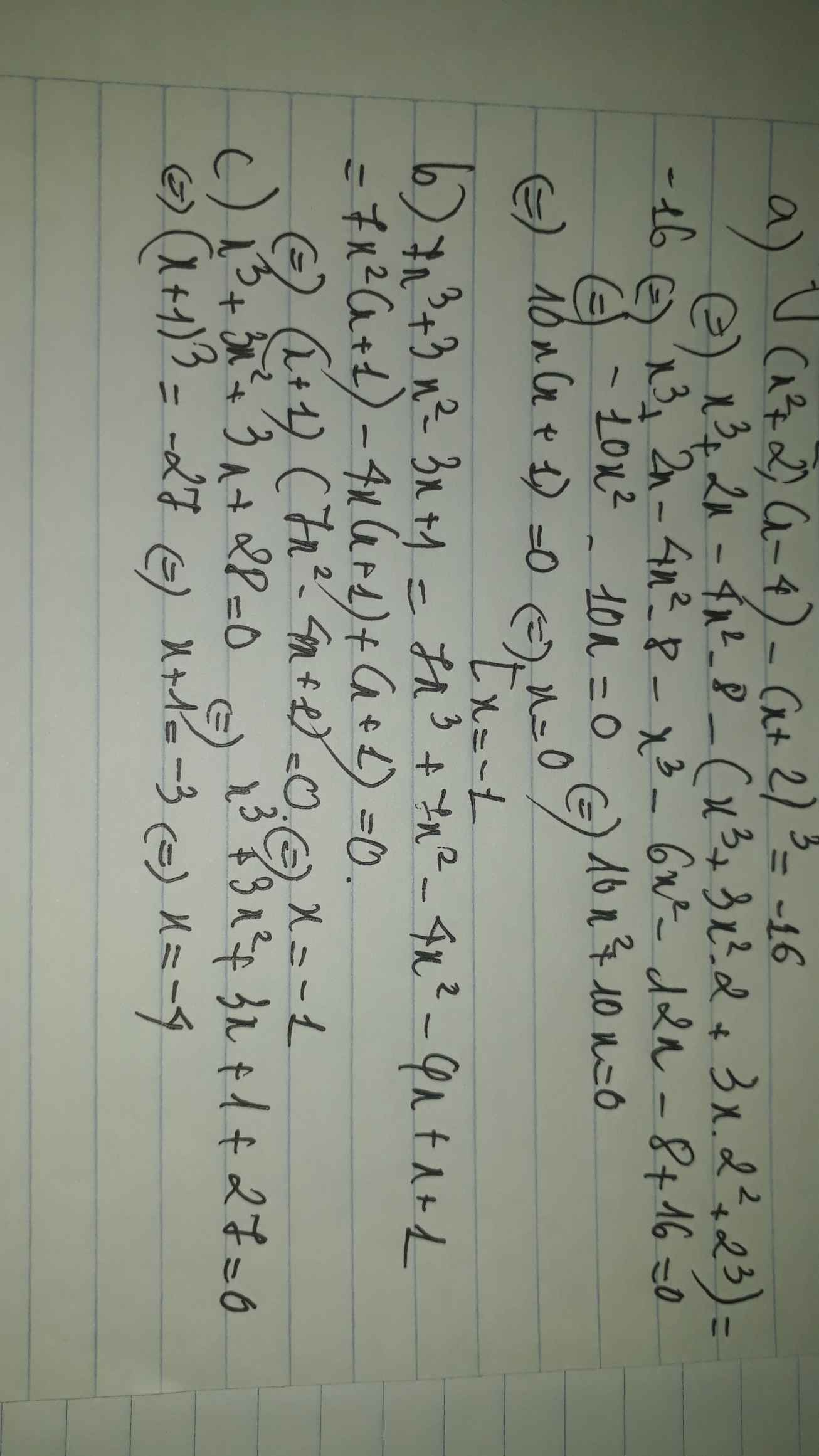Tìm x, biết x^3 + 3x^2 +3x +28 =0

Những câu hỏi liên quan
Tìm x biết a) x(x-25)=0 b)2x(x-4)-x(2x-1)=-28 c)x^2 -5x=0 d)(x-2)^2-(x+1)(x+3)=-7 e)(3x+5).(4-3x)=0 f)x^2-1/4=0
a: \(x\in\left\{0;25\right\}\)
c: \(x\in\left\{0;5\right\}\)
Đúng 1
Bình luận (0)
tìm x thỏa mãn:
a) (x2+2)(x-4)-(x+2)3=-16
b) 7x3+3x2-3x+1=0
c) x3+3x2+3x+28=0
a: Ta có: \(\left(x^2+2\right)\left(x-4\right)-\left(x+2\right)^3=-16\)
\(\Leftrightarrow x^3-4x^2+2x-8-x^3-6x^2-12x-8=-16\)
\(\Leftrightarrow-10x^2-10x=0\)
\(\Leftrightarrow-10x\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
c: Ta có: \(x^3+3x^2+3x+28=0\)
\(\Leftrightarrow\left(x+1\right)^3=-27\)
\(\Leftrightarrow x+1=-3\)
hay x=-4
Đúng 0
Bình luận (0)
Tìm x, biết:
a) 7x2 - 28 = 0
b) \(\dfrac{2}{3}\)x(x2 - 4) = 0
c) 2x(3x - 5) - (5 - 3x) = 0
d) (2x - 1)2 - 25 = 0
a) Ta có: \(7x^2-28=0\)
\(\Leftrightarrow7\left(x^2-4\right)=0\)
\(\Leftrightarrow7\left(x-2\right)\left(x+2\right)=0\)
mà 7>0
nên (x-2)(x+2)=0
hay \(\left[{}\begin{matrix}x-2=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
Vậy: \(x\in\left\{2;-2\right\}\)
b) Ta có: \(\dfrac{2}{3}x\left(x^2-4\right)=0\)
\(\Leftrightarrow\dfrac{2}{3}x\left(x-2\right)\left(x+2\right)=0\)
mà \(\dfrac{2}{3}>0\)
nên x(x-2)(x+2)=0
hay \(\left[{}\begin{matrix}x=0\\x-2=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
Vậy: \(x\in\left\{0;-2;2\right\}\)
c) Ta có: \(2x\left(3x-5\right)-\left(5-3x\right)=0\)
\(\Leftrightarrow2x\left(3x-5\right)+\left(3x-5\right)=0\)
\(\Leftrightarrow\left(3x-5\right)\left(2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-5=0\\2x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=5\\2x=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\\x=-\dfrac{1}{2}\end{matrix}\right.\)
Vậy: \(x\in\left\{\dfrac{5}{3};-\dfrac{1}{2}\right\}\)
d) Ta có: \(\left(2x-1\right)^2-25=0\)
\(\Leftrightarrow\left(2x-1-5\right)\left(2x-1+5\right)=0\)
\(\Leftrightarrow\left(2x-6\right)\left(2x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-6=0\\2x+4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=6\\2x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)
Vậy: \(x\in\left\{3;-2\right\}\)
Đúng 0
Bình luận (0)
a,7x2 - 28 = 0
=> 7x2 = 28 => x2 = 4 => x = 2
b,2/3x(x2 - 4) = 0
=>2/3x(x - 2)(x + 2) = 0
=> x ∈ {0 ; 2 ; -2}
c,2x(3x - 5) - (5 - 3x) = 0
= 2x(3x - 5) + (3x - 5)
= (3x - 5)(2x + 1) = 0
=> x ∈ { 5/3 ; -1/2}
d, (2x - 1)2 - 25 = 0
=> (2x - 4)(2x - 6) = 0
=> x ∈ {2 ;3}
Đúng 0
Bình luận (0)
a,7x2 - 28 = 0
=> 7x2 = 28 => x2 = 4 => x = 2
b,2/3x(x2 - 4) = 0
=>2/3x(x - 2)(x + 2) = 0
=> x ∈ {0 ; 2 ; -2}
c,2x(3x - 5) - (5 - 3x) = 0
= 2x(3x - 5) + (3x - 5)
= (3x - 5)(2x + 1) = 0
=> x ∈ { 5/3 ; -1/2}
d, (2x - 1)2 - 25 = 0
=> (2x - 4)(2x - 6) = 0
=> x ∈ {2 ;3}
Đúng 0
Bình luận (0)
Bài 1: Tìm x, biết:
a) (x+3)^3-x(3x+1)^2+(2x+1) (4x^2-2x+1)=28
b) (x^2-1)^3-(x^4+x^2+1) (x^2-1)=0
a) (x + 3)3 - x(3x + 1)2 + (2x + 1)(4x2 - 2x + 1) = 28
=> x3 + 9x2 + 27x + 27 - x(9x2 + 6x + 1) +(2x + 1)[(2x)2 - 2.x.1 + 12 ] = 28
=> x3 + 9x2 + 27x + 27 - 9x3 - 6x2 - x + (2x)3 + 13 = 28
=> x3 + 9x2 + 27x + 27 - 9x3 - 6x2 - x + 8x3 + 1 = 28
=> (x3 - 9x3 + 8x3) + (9x2 - 6x2) + (27x - x) + (27 + 1) = 28
=> 3x2 + 26x + 28 = 28
=> 3x2 + 26x = 0
=> 3x2 + 26x = 0
=> \(3x\left(x+\frac{26}{3}\right)=0\)
=> 3x = 0 hoặc x + 26/3 = 0
=> x = 0 hoặc x = -26/3
b) \(\left(x^2-1\right)^3-\left(x^4+x^2+1\right)\left(x^2-1\right)=0\)
=> \(x^6-3x^4+3x^2-1-\left(x^6-1\right)=0\)
=> \(x^6-3x^4+3x^2-1-x^6+1=0\)
=> \(\left(x^6-x^6\right)-3x^4+3x^2+\left(-1+1\right)=0\)
=> \(-3x^4+3x^2=0\)
=> \(-\left(3x^4-3x^2\right)=0\)
=> \(3x\left(x^3-x\right)=0\)
=> \(\orbr{\begin{cases}3x=0\\x^3-x=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x\left(x^2-1\right)=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x^2-1=0\end{cases}}\)
=> \(\orbr{\begin{cases}x=0\\x=\pm1\end{cases}}\)
Bài 1: Tìm x biết a) x^3 - 4x^2 - x + 4= 0 b) x^3 - 3x^2 + 3x + 1=0 c) x^3 + 3x^2 - 4x - 12=0 d) (x-2)^2 - 4x +8 =0
a: \(x^3-4x^2-x+4=0\)
=>\(\left(x^3-4x^2\right)-\left(x-4\right)=0\)
=>\(x^2\left(x-4\right)-\left(x-4\right)=0\)
=>\(\left(x-4\right)\left(x^2-1\right)=0\)
=>\(\left[{}\begin{matrix}x-4=0\\x^2-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x^2=1\end{matrix}\right.\Leftrightarrow x\in\left\{2;1;-1\right\}\)
b: Sửa đề: \(x^3+3x^2+3x+1=0\)
=>\(x^3+3\cdot x^2\cdot1+3\cdot x\cdot1^2+1^3=0\)
=>\(\left(x+1\right)^3=0\)
=>x+1=0
=>x=-1
c: \(x^3+3x^2-4x-12=0\)
=>\(\left(x^3+3x^2\right)-\left(4x+12\right)=0\)
=>\(x^2\cdot\left(x+3\right)-4\left(x+3\right)=0\)
=>\(\left(x+3\right)\left(x^2-4\right)=0\)
=>\(\left(x+3\right)\left(x-2\right)\left(x+2\right)=0\)
=>\(\left[{}\begin{matrix}x+3=0\\x-2=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=2\\x=-2\end{matrix}\right.\)
d: \(\left(x-2\right)^2-4x+8=0\)
=>\(\left(x-2\right)^2-\left(4x-8\right)=0\)
=>\(\left(x-2\right)^2-4\left(x-2\right)=0\)
=>\(\left(x-2\right)\left(x-2-4\right)=0\)
=>(x-2)(x-6)=0
=>\(\left[{}\begin{matrix}x-2=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=6\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tìm x
(3x+5)(4-3x)=0
3x(x-7)-2(x-7)=0
7x2-28=0
(2x+1)+x(2x+1)=0
(Ko chép lại đề)
\(a.\Rightarrow\orbr{\begin{cases}3x+5=0\\4-3x=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=-\frac{5}{3}\\x=\frac{4}{3}\end{cases}}\)
\(b.\left(3x-2\right)\left(x-7\right)=0\)
\(\Rightarrow\orbr{\begin{cases}3x-2=0\\x-7=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{2}{3}\\x=7\end{cases}}\)
\(c.7x^2=28\)
\(x^2=4\)
\(x^2=2^2\)
\(x=\pm2\)
\(d.\left(2x+1\right)\left(1+x\right)=0\)
\(\Rightarrow\orbr{\begin{cases}2x+1=0\\1+x=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=-\frac{1}{2}\\x=-1\end{cases}}\)
a)\(\left(3x+5\right)\left(4-3x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}3x+5=0\\4-3x=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-\frac{5}{3}\\x=\frac{4}{3}\end{cases}}}\)
b)\(3x\left(x-7\right)-2\left(x-7\right)=0\)
\(\Leftrightarrow\left(x-7\right)\left(3x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-7=0\\3x-2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=7\\x=\frac{2}{3}\end{cases}}}\)
c) \(7x^2-28=0\)
\(\Leftrightarrow7x^2=28\)
\(\Leftrightarrow7x^2=7.4\)
\(\Leftrightarrow x^2=4\)
\(\Leftrightarrow x=\pm2\)
d)\(\left(2x+1\right)+x\left(2x+1\right)=0\)
\(\Leftrightarrow\left(2x+1\right)\left(1+x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x+1=0\\1+x=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-\frac{1}{2}\\x=-1\end{cases}}}\)
#H
x^3+3x^2+3x+28=0
\(\Leftrightarrow x^3+3x^2+3x+1+27=0\\ \Leftrightarrow\left(x+1\right)^3+27=0\\ \Leftrightarrow\left(x+4\right)\left(x^2+2x+1-3x-3+9\right)=0\\ \Leftrightarrow\left(x+4\right)\left(x^2-x+7\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-4\\\left(x-\dfrac{1}{2}\right)^2+\dfrac{27}{4}=0\left(vn\right)\end{matrix}\right.\Leftrightarrow x=-4\)
Đúng 3
Bình luận (0)
Tìm x:
a) (3x+4)(4-x)=0
b) 3x(x-4)-2(x-4)=0
c) 7x2-28=0
a) \(\left(3x+4\right)\left(4-x\right)=0\Rightarrow\orbr{\begin{cases}3x+4=0\\4-x=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}3x=\left(-4\right)\Rightarrow x=\frac{-4}{3}\\x=4\end{cases}}\)
\(\Rightarrow x=\left\{\frac{-4}{3};4\right\}\)
b) \(\Rightarrow\orbr{\begin{cases}3\left(x-4\right)=0\\2\left(x-4\right)=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x-4=0\\x-4=0\end{cases}}\Rightarrow x=4\)
c) => 7x2=0+28
=> x2=28:7
=> x2=4
=> x2=22= (-2)2
=> x={-2;2}
Đúng 0
Bình luận (0)
1) tính nhanh giá trị biểu thức:a) x^2 + 4y^2 - 4xy tại x18; y4b) (2x + 1)^2 + (2x - 1)^2 - 2 (1 + 2x) (1 - 2x) tại x 100 2) tìm x biết : a) 7x^2 -28 0 b) 2/3x (x^2 - 4) 0 c) 2x (3x - 5) - (5 - 3x) 0 d) (2x - 1)^2 -25 0 3) phân tích các đa thức sau thành nhân tử :a) 2(x - 3) - y (x - 3) b) x^3 + 3x^2 - 3x - 1 c) x^2 + 5xy d) x^2 - x - y^2 -ye) x^2 - 9y^2 +2x +1 ...
Đọc tiếp
1) tính nhanh giá trị biểu thức:
a) x^2 + 4y^2 - 4xy tại x=18; y=4
b) (2x + 1)^2 + (2x - 1)^2 - 2 (1 + 2x) (1 - 2x) tại x = 100
2) tìm x biết :
a) 7x^2 -28 =0 b) 2/3x (x^2 - 4) = 0 c) 2x (3x - 5) - (5 - 3x) = 0
d) (2x - 1)^2 -25 = 0
3) phân tích các đa thức sau thành nhân tử :
a) 2(x - 3) - y (x - 3) b) x^3 + 3x^2 - 3x - 1 c) x^2 + 5xy d) x^2 - x - y^2 -y
e) x^2 - 9y^2 +2x +1 f) x^2 - 2x - 4y^2 - 4y g) 10x +15y h) x^2 - 2xy + y^2 - 4
i) 4x - 4y + x^2 - 2xy + y^2 k) x^4 - 4x^3 - 8x^2 - 8x l) x^3 + x^2 - 4x - 4
n) x^3 + x^2y - xy^2 - y^3 o) x^2 - y^2 - 2x - 2y p) x^2 - y^2 - 2x + 2y
q) 2x + 2y - x^2 - xy r) x^2 - 25 + y^2 + 2xy s) x^3 - 2x^2 + x
t) 12x^2y - 18xy^2 - 30y^2 u) 36 - 12x + x^2 v) 3x^2 - 3xy
Bài 2:
a: \(\Leftrightarrow\left(x-2\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
Đúng 0
Bình luận (0)