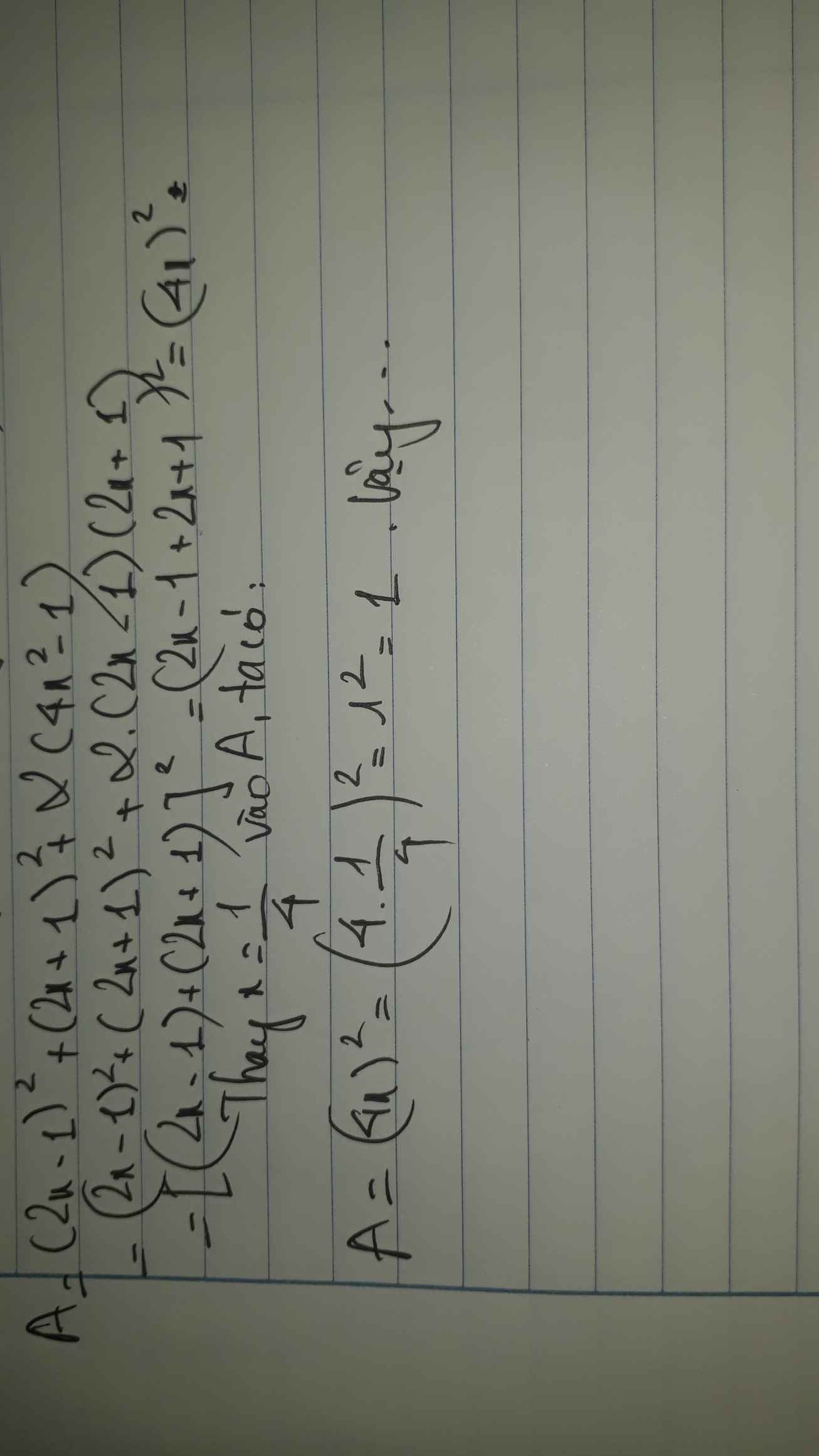Tính giá trị của biểu thức sau : (1 + 1 / (1 ^ 2))(1 + 1 / (2 ^ 2)) ...(1+1/n^ 2 ) python

Những câu hỏi liên quan
Tính giá trị của biểu thức sau : (1+1/1^2)…(1+1/n^2)
Program HOC24;
var i,n: integer;
S: real;
begin
write('Nhap n: '); readln(n);
s:=0;
for i:=1 to n do s:=s+(1+1/sqr(i));
write('Gia tri cua bieu thuc do la: ',s:6:2);
readln
end.
Đúng 1
Bình luận (0)
Tính giá trị của biểu thức sau :
N = 1/2 + 1/3 + 1/4 + ..............+ 1/9 + 1/ 10
1/N = 1: (1/2 +1/3 + 1/4 + .....+ 1/10)
=> 1/N = 2+3+4+...+10
=> 1/N= (10+2). 9/2= 54
=> N = 1/54
nhớ k cho mình nha :33
Bài 8. a) Tính giá trị của biểu thức 0x2y4z + 7/2x2y4z – 2/5x2y4z tại x 2 ; y 1/2 ; z -1.a) Tính giá trị của biểu thức 2/5x4z3y – 0x4z3y + x4z3y tại x 2 ; y 1/2 ; z -1.b) Tính giá trị của biểu thức xy3 + 5xy3 + ( - 7xy3) tại c) Tính giá trị của biểu thức tại x 3, y -1/2
Đọc tiếp
Bài 8. a) Tính giá trị của biểu thức 0x2y4z + 7/2x2y4z – 2/5x2y4z tại x = 2 ; y =1/2 ; z = -1.
a) Tính giá trị của biểu thức 2/5x4z3y – 0x4z3y + x4z3y tại x = 2 ; y =1/2 ; z = -1.
b) Tính giá trị của biểu thức xy3 + 5xy3 + ( - 7xy3) tại
c) Tính giá trị của biểu thức tại x = 3, y = -1/2
a: \(A=0x^2y^4z+\dfrac{7}{2}x^2y^4z-\dfrac{2}{5}x^2y^4z=\dfrac{31}{10}x^2y^4z=\dfrac{31}{10}\cdot2^2\cdot\dfrac{1}{16}\cdot\left(-1\right)=-\dfrac{31}{40}\)
a: \(=\dfrac{7}{5}x^4z^3y=\dfrac{7}{5}\cdot2^4\cdot\left(-1\right)^3\cdot\dfrac{1}{2}=-\dfrac{56}{5}\)
b: \(=-xy^3\)
Đúng 0
Bình luận (0)
1. Tính Giá trị nhỏ nhất của biểu thứ (x+1)(x+2)(x+3)(x+6)+2010
2. Phân tích đa thức thành nhân tử (x-2)(x-4)(x-6)(x-8) +15
3. Tính giá trị biểu thức sau: x^2 +y= y^2 +x. tính giá trị của biểu thức sau A= (x^2 +y^2 +xy) : (xy-1)
bbgfhfygfdsdty64562gdfhgvfhgfhhhhh
\hvhhhggybhbghhguyg
tính giá trị của biểu thức sau: a=(2x-1)^2+(2x+1)^2+2(4x^2-1) tại x=1/4
Ta có: \(a=\left(2x-1\right)^2+\left(2x+1\right)^2+2\left(4x^2-1\right)\)
\(=\left(2x-1+2x+1\right)^2\)
\(=16x^2=16\cdot\dfrac{1}{16}=1\)
Đúng 0
Bình luận (0)
B=m(m-n+1)-n(n+1-m) với m= -\(\dfrac{2}{3}\) n= -\(\dfrac{1}{3}\)
tính giá trị của các biểu thức sau
\(B=m^2-mn+m-n^2-n+mn=m^2-n^2+n-n\\ =\left(m-n\right)\left(m+n+1\right)\\ =\left(-\dfrac{2}{3}+\dfrac{1}{3}\right)\left(-\dfrac{2}{3}-\dfrac{1}{3}+1\right)=-\dfrac{1}{3}\cdot0=0\)
Đúng 2
Bình luận (0)
B=m(m-n+1)-n(n+1-m) với m= -\(\dfrac{2}{3}\)n= -\(\dfrac{1}{3}\)
tính giá trị của các biểu thức sau
B=m(m-n+1)-n(n+1-m) với m= -\(\dfrac{2}{3}\) n= -\(\dfrac{1}{3}\)
tính giá trị của các biểu thức sau
B=m(m-n+1)-n(n+1-m) với m= -\(\dfrac{2}{3}\)n= -\(\dfrac{1}{3}\)
tính giá trị của các biểu thức sau
\(B=m\left(m-n+1\right)-n\left(n+1-m\right)=m^2-mn+m-n^2-n+mn=m^2-n^2+m-n=\left(m-n\right)\left(m+n\right)+\left(m-n\right)=\left(m-n\right)\left(m+n+1\right)=\left(-\dfrac{2}{3}+\dfrac{1}{3}\right)\left(-\dfrac{2}{3}-\dfrac{1}{3}+1\right)=-\dfrac{1}{3}.0=0\)
Đúng 1
Bình luận (0)