Cho \(\Delta ABC\). Từ A, kẻ đường thẳng vuông góc với BC tại D. Gọi E; F lần lượt là trung điểm của AC và BC. Chứng minh đường thẳng EF cắt đoạn thẳng AD tại trung điểm của đoạn thẳng đó.

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có ACAB. Đường cao AH. Từ H kẻ HDperpAB (DinAB), HEperpAC( EinAC).a. Chứng minh: Delta AEDsimDelta ABCb. Gọi M là điểm đối xứng của B qua H. Từ M kẻ đường thẳng vuông góc với BC cắt cạnh AC tại N. Chứng minh rằng DE song song với BNd.Chứng minh rằng: dfrac{AB^3}{AC^3}dfrac{BD}{CE}--- Giúp minh với ạ, mai mình nộp rồiT.T
Đọc tiếp
Cho tam giác ABC vuông tại A có AC>AB. Đường cao AH. Từ H kẻ HD\(\perp\)AB (D\(\in\)AB), HE\(\perp\)AC( E\(\in\)AC).
a. Chứng minh: \(\Delta AED\sim\Delta ABC\)
b. Gọi M là điểm đối xứng của B qua H. Từ M kẻ đường thẳng vuông góc với BC cắt cạnh AC tại N. Chứng minh rằng DE song song với BN
d.Chứng minh rằng: \(\dfrac{AB^3}{AC^3}=\dfrac{BD}{CE}\)
---> Giúp minh với ạ, mai mình nộp rồiT.T
Sau gần một buổi trưa lăn lội với Thales, đồng dạng ở câu b thì t đã nghĩ đến cách của lớp 7 ~ ai dè làm được ^^
Đúng 0
Bình luận (1)
Sao bổ sung hình vẽ không được vậy nè
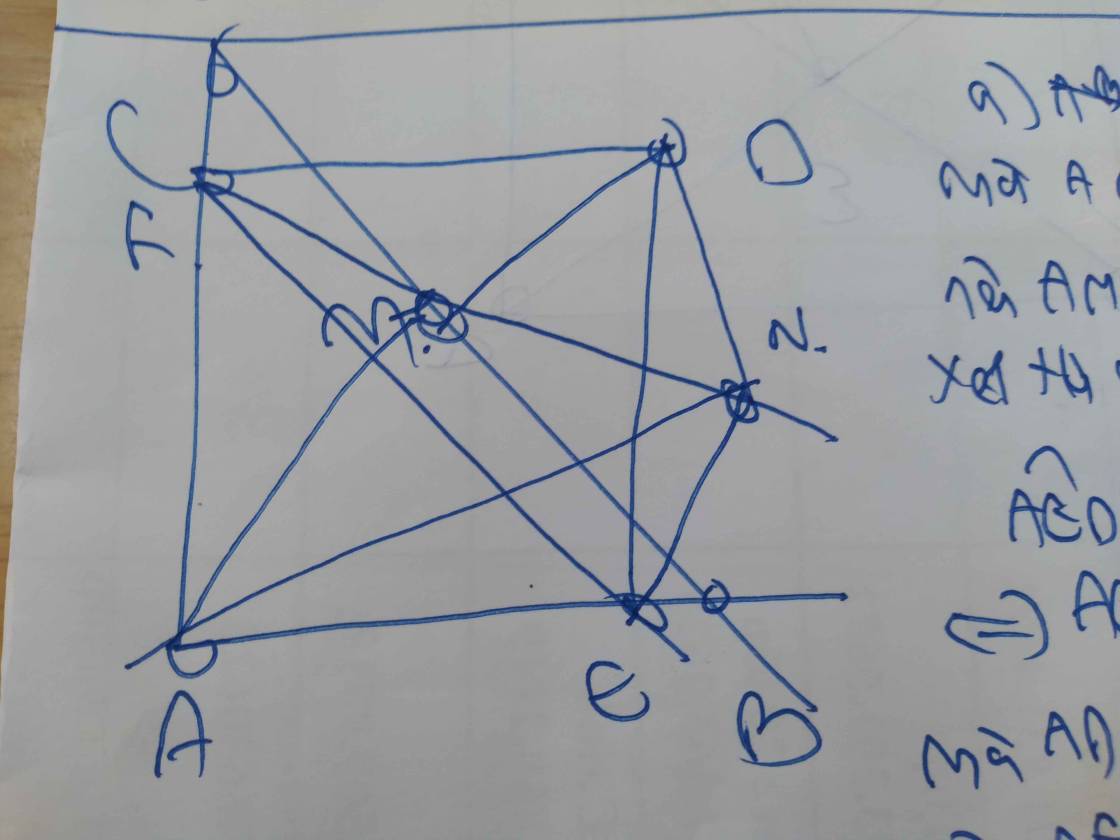
Cho Delta ABC cân tại A. Trên cạnh BC lấy điểm D ( D khác B,C ). Trên tia đối của tia CB lấy điểm E sao cho CEBD. Đường vuông góc với BC kẻ từ D cắt BA tại M. Đường vuông góc với BC kẻ từ E cắt tia AC tại I.a) Chứng minh rằng: DMENb) Chứng minh rằng: IMIN; BCMNc) Gọi O là giao của đường phân giác góc A và đường thẳng vuông góc với MN tại I. Chứng minh rằng: Delta BMODelta CNO. Từ đó suy ra điểm O cố định.
Đọc tiếp
Cho \(\Delta ABC\) cân tại A. Trên cạnh BC lấy điểm D ( D khác B,C ). Trên tia đối của tia CB lấy điểm E sao cho CE=BD. Đường vuông góc với BC kẻ từ D cắt BA tại M. Đường vuông góc với BC kẻ từ E cắt tia AC tại I.
a) Chứng minh rằng: DM=EN
b) Chứng minh rằng: IM=IN; BC<MN
c) Gọi O là giao của đường phân giác góc A và đường thẳng vuông góc với MN tại I. Chứng minh rằng: \(\Delta BMO=\Delta CNO\). Từ đó suy ra điểm O cố định.
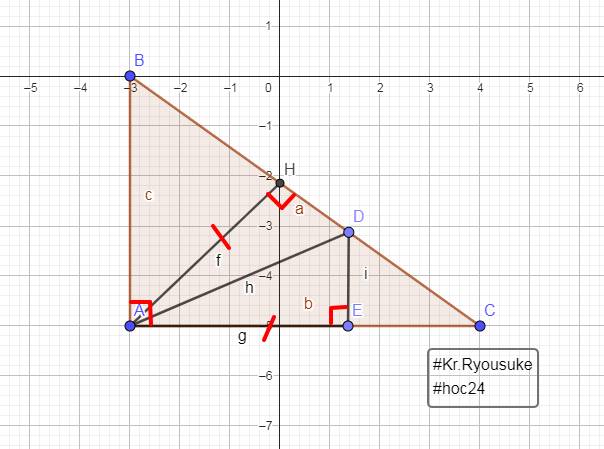
Bài 4. (2,5 điểm) Cho tam giác ABC vuông tại A (AB < AC), đường cao AH. Trên cạnh ^ C lfy điểm E sao cho AH = AE Từ E kẻ đường thẳng vuông góc với AC, cắt BC tại D. a) Chimg minh Delta*AHD = Delta*AED b) So sinh DH và DC c) Gọi K là giao điểm của DE và AH. Chứng minh AD KC
`a,`
Xét `2 \Delta` vuông `AHD` và ` AED`:
\(\text{AD chung}\)
\(\text{AH = AE (gt)}\)
`=> \Delta AHD = \Delta AED (ch-cgv)`
`b,`
Vì `\Delta AHD = \Delta AED (a)`
`->`\(\text{DH = DE (2 cạnh tương ứng) (1)}\)
\(\text{Xét }\Delta\text{DEC :}\)
\(\widehat{\text{DEC}}=90^0\)
`@` Theo định lý quan hệ giữa góc và cạnh đối diện
`->`\(\text{DC là cạnh lớn nhất}\)
`->`\(\text{DC > DE (2)}\)
Từ \(\left(1\right)\) và \(\left(2\right)\)
`->`\(\text{DC > DH.}\)
`c,` cho mình bỏ câu này;-;;; xin lỗi cậu nhiều;-;.
Đúng 0
Bình luận (0)
cho tam giác abc vuông tại a .gọi g là trung điểm bc từ g kẻ ge vuông góc với ab ,gf vuông góc ac từ e kẻ đường thẳng song song với bf đường thẳng này cắt bf tại i cho tam giác abc vuông tại a .gọi g là trung điểm bc từ g kẻ ge vuông góc với ab ,gf vuông góc ac từ e kẻ đường thẳng song song với bf đường thẳng này cắt bf tại i A chứng minh tứ giác AEFG là hình chữ nhật B chứng minh tứ giác BEIF là hình bình hành C chứng minh tứ giác AGCI là hình thoi
Đọc tiếp
cho tam giác abc vuông tại a .gọi g là trung điểm bc từ g kẻ ge vuông góc với ab ,gf vuông góc ac từ e kẻ đường thẳng song song với bf đường thẳng này cắt bf tại i cho tam giác abc vuông tại a .gọi g là trung điểm bc từ g kẻ ge vuông góc với ab ,gf vuông góc ac từ e kẻ đường thẳng song song với bf đường thẳng này cắt bf tại i A chứng minh tứ giác AEFG là hình chữ nhật B chứng minh tứ giác BEIF là hình bình hành C chứng minh tứ giác AGCI là hình thoi
Sửa đề: Từ E kẻ đường thẳng song song với BF, cắt GF tại I
a: Xét tứ giác AEGF có
\(\widehat{AEG}=\widehat{AFG}=\widehat{FAE}=90^0\)
Do đó: AEGF là hình chữ nhật
b: AEGF là hình chữ nhật
=>GF//AE và GF=AE
Ta có: GF//AE
I\(\in\)FG
Do đó: FI//AE
Ta có: FI//AE
E\(\in\)AB
Do đó: FI//EB
Xét tứ giác FIEB có
FI//EB
FB//EI
Do đó: FIEB là hình bình hành
c: Xét ΔABC có
G là trung điểm của BC
GE//AC
Do đó: E là trung điểm của AB
=>EA=EB(1)
Xét ΔABC có
G là trung điểm của BC
GF//AB
Do đó: F là trung điểm của AC
AEGF là hình chữ nhật
=>AE=GF(2)
FIEB là hình bình hành
=>FI=EB(3)
Từ (1),(2),(3) suy ra FI=FG
=>F là trung điểm của GI
Xét tứ giác AGCI có
F là trung điểm chung của AC và GI
nên AGCI là hình bình hành
Hình bình hành AGCI có AC\(\perp\)GI
nên AGCI là hình thoi
Đúng 2
Bình luận (0)
cho tam giác ABC vuông cân tại A. Gọi M là trung điểm BC. Trên tia đối MA lấy điểm D từ D kẻ đường thẳng vuông góc với AB, AC lần lượt tại E, F a) c/m tg AEDF là hình vuông. b) c/m EF // BC. c) Qua E kẻ đường thẳng vuông góc với
a: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là phân giác của góc BAC
Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
=>AEDF là hình chữ nhật
Hình chữ nhật AEDF có AD là phân giác của góc FAE
nên AEDF là hình vuông
b: AEDF là hình vuông
=>\(\widehat{AEF}=45^0\)
=>\(\widehat{AEF}=\widehat{ABC}\left(=45^0\right)\)
mà hai góc này là hai góc ở vị trí đồng vị
nên FE//BC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH (H \(\in\) BC). Qua B kẻ đường thẳng vuông góc với BC tại B, cắt AC tại D. Gọi K là hình chiếu của A trên BD. Chứng minh rằng BK.BD = BH.BC, từ đó suy ra \(\Delta\)BHK \(\backsim\) \(\Delta\)BDC
ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\left(1\right)\)
Xét ΔABD vuông tại A có AK là đường cao
nên \(BK\cdot BD=BA^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BC=BK\cdot BD\)
=>\(\dfrac{BH}{BD}=\dfrac{BK}{BC}\)
Xét ΔBHK và ΔBDC có
\(\dfrac{BH}{BD}=\dfrac{BK}{BC}\)
\(\widehat{HBK}\) chung
Do đó: ΔBHK đồng dạng với ΔBDC
Đúng 3
Bình luận (0)
Cho Delta ABCvuông tại A. Trên cạnh AC lấy điểm E ( E không trùng với các điểm A, C). Qua E kẻ đường thẳng d vuông góc với BC tại F và đường thẳng d cắt BA tại K.a, Cm: Delta CEF~Delta CABb, Cm: BA.BK BF.BCc, Cm: góc BAF góc BCKd, Gọi M là trung điểm của CK, qua B kẻ đường vuông góc với BM cắt các tia CA và KF lần lượt tại P và Q.Cm: BQ BP
Đọc tiếp
Cho \(\Delta ABC\)vuông tại A. Trên cạnh AC lấy điểm E ( E không trùng với các điểm A, C). Qua E kẻ đường thẳng d vuông góc với BC tại F và đường thẳng d cắt BA tại K.
a, Cm: \(\Delta CEF~\Delta CAB\)
b, Cm: BA.BK = BF.BC
c, Cm: góc BAF = góc BCK
d, Gọi M là trung điểm của CK, qua B kẻ đường vuông góc với BM cắt các tia CA và KF lần lượt tại P và Q.
Cm: BQ = BP
a) Xét \(\Delta CEF\)và \(\Delta CAB\)có:
\(\widehat{CFE}=\widehat{CBA}\left(=90^0\right)\).
\(\widehat{BCA}\)chung.
\(\Rightarrow\Delta CEF~\Delta CAB\left(g.g\right)\)(điều phải chứng minh).
b) Xét \(\Delta ABC\)và \(\Delta FBK\)có:
\(\widehat{KBC}\)chung.
\(\widehat{BAC}=\widehat{BFK}\left(=90^0\right)\).
\(\Rightarrow\Delta ABC~\Delta FBK\left(g.g\right)\).
\(\Rightarrow\frac{BA}{BF}=\frac{BC}{BK}\)(tỉ số đồng dạng).
\(\Rightarrow BA.BK=BF.BC\)(điều phải chứng minh).
c) Ta có: \(\frac{BA}{BF}=\frac{BC}{BK}\)(theo câu a)).
\(\Rightarrow\frac{BA}{BC}=\frac{BF}{BK}\)(tính chất của tỉ lệ thức).
Xét \(\Delta BAF\)và \(\Delta BCK\)có:
\(\frac{BA}{BC}=\frac{BF}{BK}\)(chứng minh trên).
\(\widehat{KBC}\)chung.
\(\Rightarrow\Delta BAF~\Delta BCK\left(c.g.c\right)\).
\(\Rightarrow\widehat{BAF}=\widehat{BCK}\)(2 góc tương ứng) (điều phải chứng minh).
Xem thêm câu trả lời
Cho Delta ABC vuông tại A, qua C kẻ đường thẳng d vuông góc với AC. Trên d lấy điểm E sao cho CE AB( E và B thuộc hai nửa phẳng đối nhau bờ AC)a) Vẽ hìnhb) C/m BC // AE và BC AEc) Gọi I là trung điểm của AC, qua I kẻ đường thẳng song song với d cắt BC tại M. C/m MI là tia phân giác của góc AMCd) Biết góc widehat{ABC} 60 độ. Tính số đo của góc widehat{BAM}e) C/m: ba điểm B, I, E thẳng hàng
Đọc tiếp
Cho \(\Delta ABC\) vuông tại A, qua C kẻ đường thẳng d vuông góc với AC. Trên d lấy điểm E sao cho CE = AB( E và B thuộc hai nửa phẳng đối nhau bờ AC)
a) Vẽ hình
b) C/m BC // AE và BC = AE
c) Gọi I là trung điểm của AC, qua I kẻ đường thẳng song song với d cắt BC tại M. C/m MI là tia phân giác của góc AMC
d) Biết góc \(\widehat{ABC}\) = 60 độ. Tính số đo của góc \(\widehat{BAM}\)
e) C/m: ba điểm B, I, E thẳng hàng
a: 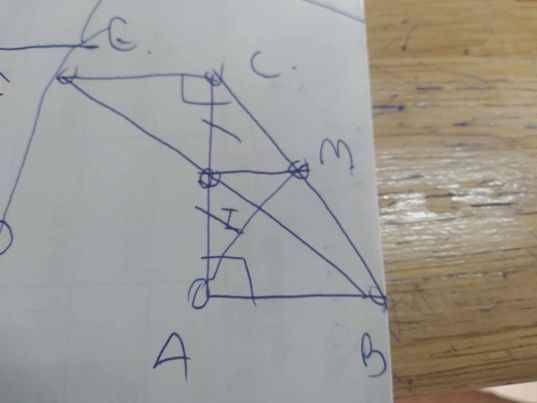
b:
Ta có: CE\(\perp\)CA
AB\(\perp\)CA
Do đó: CE//AB
Xét ΔCEB và ΔABE có
CE=AB
\(\widehat{CEB}=\widehat{ABE}\)(hai góc so le trong, AB//CE)
BE chung
Do đó: ΔCEB=ΔABE
=>CB=AE
Ta có: ΔCEB=ΔABE
=>\(\widehat{CBE}=\widehat{AEB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên CB//AE
c: MI//CE
CE//AB
Do đó: MI//AB
Ta có: MI//AB
AB\(\perp\)AC
Do đó: MI\(\perp\)AC
Xét ΔMAC có
MI là đường cao
MI là đường trung tuyến
Do đó: ΔMAC cân tại M
Ta có: ΔMAC cân tại M
mà MI là đường cao
nên MI là phân giác của \(\widehat{AMC}\)
d: Ta có: \(\widehat{MAC}+\widehat{MAB}=\widehat{BAC}=90^0\)
\(\widehat{MCA}+\widehat{MBA}=90^0\)(ΔABC vuông tại A)
mà \(\widehat{MAC}=\widehat{MCA}\)(ΔAMC cân tại M)
nên \(\widehat{MAB}=\widehat{MBA}\)
=>ΔMAB cân tại M
Xét ΔMAB cân tại M có \(\widehat{MBA}=60^0\)
nên ΔMAB đều
=>\(\widehat{BAM}=60^0\)
e: Xét ΔECI vuông tại C và ΔBAI vuông tại A có
EC=BA
CI=AI
Do đó:ΔECI=ΔBAI
=>\(\widehat{EIC}=\widehat{BIA}\)
mà \(\widehat{EIC}+\widehat{EIA}=180^0\)(hai góc kề bù)
nên \(\widehat{EIA}+\widehat{BIA}=180^0\)
=>B,I,E thẳng hàng
Đúng 3
Bình luận (0)
cho tam giác ABC vuông cân tại A. Gọi M là trung điểm BC. Trên tia đối MA lấy điểm D từ D kẻ đường thẳng vuông góc với AB, AC lần lượt tại E, F a) c/m tg AEDF là hình vuông. b) c/m EF // BC. c) Qua E kẻ đường thẳng vuông góc với MF. c/m \(\widehat{AND}\) = 40o