cho tam giác ABC cân ở A. Trên cạnh BC lấy D,E sao cho BD=CE. C/minh tam giác ADE cân

Những câu hỏi liên quan
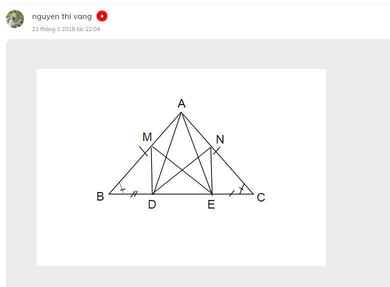
Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy hai điểm D,E sao cho BD=CE<BC/2. Đường thẳng kẻ từ D vuông góc với BC cắt AB ở M, đường thẳng kẻ từ E vuông góc với BC cắt AC ở N. Chứng minh rằng:
a) DM=EN
b) EM=DN
c) Chứng minh tam giác ADE cân.
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE, Chứng minh tam giác ADE cân.
Chứng minh được tam giác ABD = tam giác ACE (c-g-c) => AD = AE
Từ đó tam giác ADE cân tại A.
Đúng 0
Bình luận (0)
Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
Do đó: ΔABD=ΔACE
=>AD=AE
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh rằng tam giác ADE là tam giác cân ?
Hình vẽ:
Giải:
Vì tam giác \(ABC\) cân tại \(A\):
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
\(\Rightarrow\widehat{ABD}=\widehat{ACE}\) ( góc bù )
Xét \(\Delta ABD\) và \(\Delta ACE\) có:
\(AB=AC \) \(\left(gt\right)\)
\(\widehat{ABD}=\widehat{ACE}\) \(\left(cmt\right)\)
\(BD=CE \) \(\left(gt\right)\)
Do đó: \(\Delta ABD=\Delta ACE\) \(\left(c.g.c\right)\)
\(\Rightarrow AD=AE\) ( cặp cạnh tương ứng )
\(\Rightarrow\Delta ADE\) cân tại \(A\).
Đúng 2
Bình luận (0)
Bài làm
Bạn tự vẽ hình nhé
Vì tam giác ABCABC cân tại A:
⇒ˆABC=ˆACB⇒ABC^=ACB^
⇒ˆABD=ˆACE⇒ABD^=ACE^ ( góc bù )
Xét ΔABDΔABD và ΔACEΔACE có:
AB=ACAB=AC (gt)
ˆABD=ˆACEABD^=ACE^ (cmt)
BD=CEBD=CE (gt)(gt)
Do đó: ΔABD=ΔACEΔABD=ΔACE (c.g.c)(c.g.c)
⇒AD=AE⇒AD=AE ( cặp cạnh tương ứng )
⇒ΔADE⇒ΔADE cân tại A
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 8: Cho tam giác ABC, AB AC. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD CE. Chứng minh: a) Tam giác ADE cân b) ABD ACEBài 9: Cho tam giác ABC, AB AC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD AE. Gọi M là giao điểm của BE và CD. Chứng minh: a) BE CD b) BMD CME. c) AM là tia phân giác của góc BAC. giúp em bài này với ah, em cảm ơn mọi người rất nhiều ( e cần gấp lắm)
Đọc tiếp
Bài 8: Cho tam giác ABC, AB = AC. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh: a) Tam giác ADE cân b) ABD = ACE
Bài 9: Cho tam giác ABC, AB = AC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Gọi M là giao điểm của BE và CD. Chứng minh: a) BE = CD b) BMD = CME. c) AM là tia phân giác của góc BAC.
giúp em bài này với ah, em cảm ơn mọi người rất nhiều ( e cần gấp lắm)
Bài 8:
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó:ΔABD=ΔACE
Suy ra: AD=AE
b: ta có: ΔABD=ΔACE
nên \(\widehat{ADB}=\widehat{AEC}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE. Chứng minh tam giác ADE là tam giác cân
Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
Do đó: ΔABD=ΔACE
=>AD=AE
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, trên cạnh đáy BC lấy 2 điểm D và E sao cho BD=CE.Chứng minh tam giác ADE cân tại A
Ta có hình vẽ:
Xét tam giác ABD và tam giác ACE có:
AB = AC (do tam giác ABC cân)
góc ABC = góc ACB (do tam giác ABC cân)
BD = CE (GT)
Vậy tam giác ABD = tam giác ACE (c.g.c)
=> AD = AE (2 cạnh tương ứng)
=> tam giác ADE cân tại A
Đúng 0
Bình luận (2)
CHO TAM GIAC ABC CÂN TẠI A. TRÊN TIA ĐỐI CỦA BC LẤY ĐIỂM D, TRÊN TIA ĐỐI CÚA CB LẤY ĐIỂM E SAO CHO BD=CE. CHỨNG MINH TAM GIÁC ADE LÀ TAM GIÁC CÂN
tam giác ABC cân =>góc B=góc C
=>góc ABD=góc ACE (dựa vào 2 góc kề bù)
Xét tam giác ABD và tam giác ACE có
AB=AC(tam giác ABC cân)
góc ABD= góc ACE(cmt)
BD=CE(GT)
=>tam giác ABD = tam giác ACE (c-g-c)
=>AD=AE(2 cạnh tương ứng)
=>tam giác ADE cân tại A
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A trên tia đối của tia BC lấy D, trên tia đối của tia CB lấy E, sao cho BD=CE.
a) chứng minh tam giác ADE cân.
b) nếu cho thêm góc BAC = 60 độ và BD=CE=BC. tính các góc của tam giác AD
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE. Chứng minh:
a) Tam giác ADE cân
b) Tam giác ABD = tam giác ACE