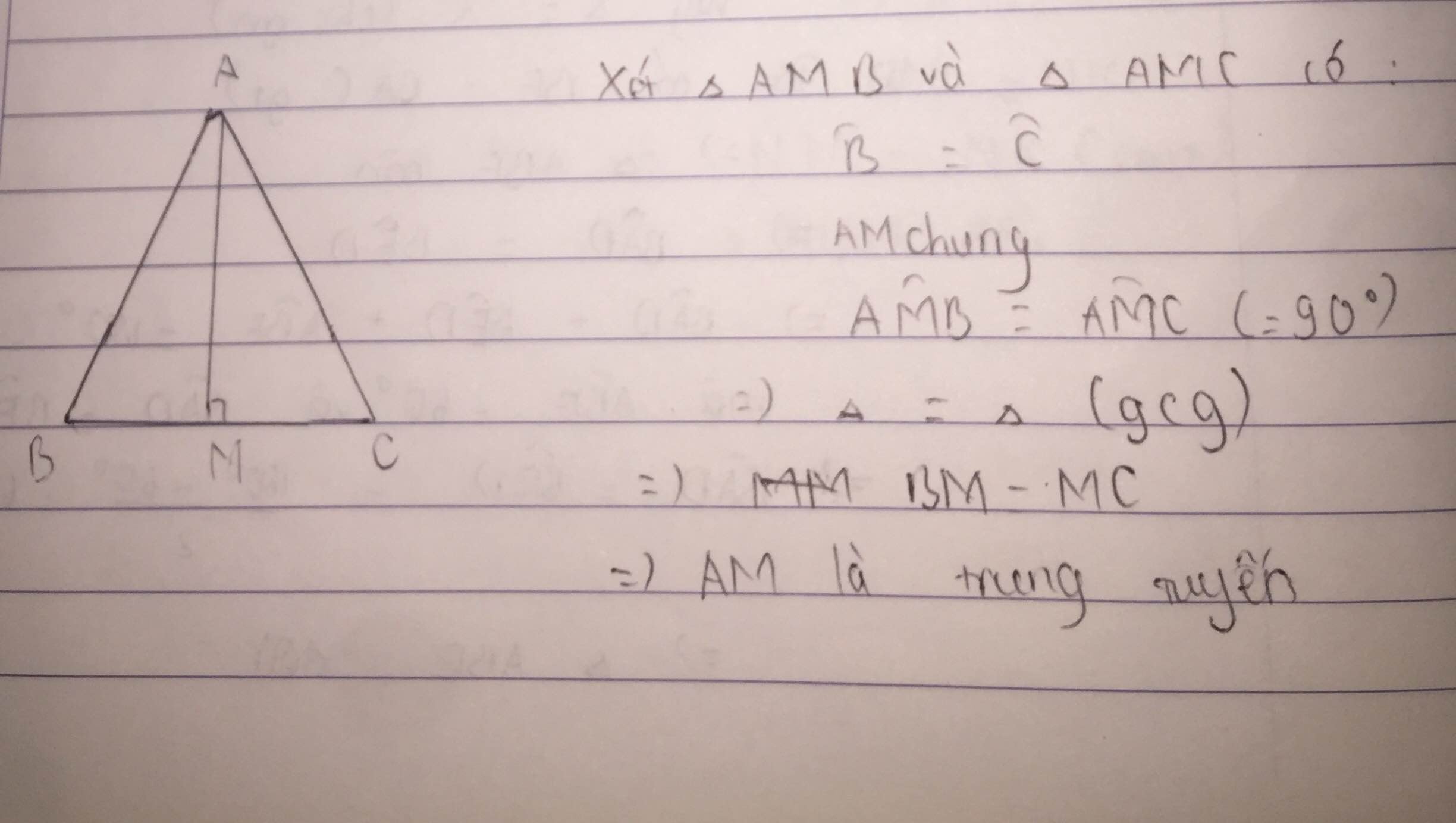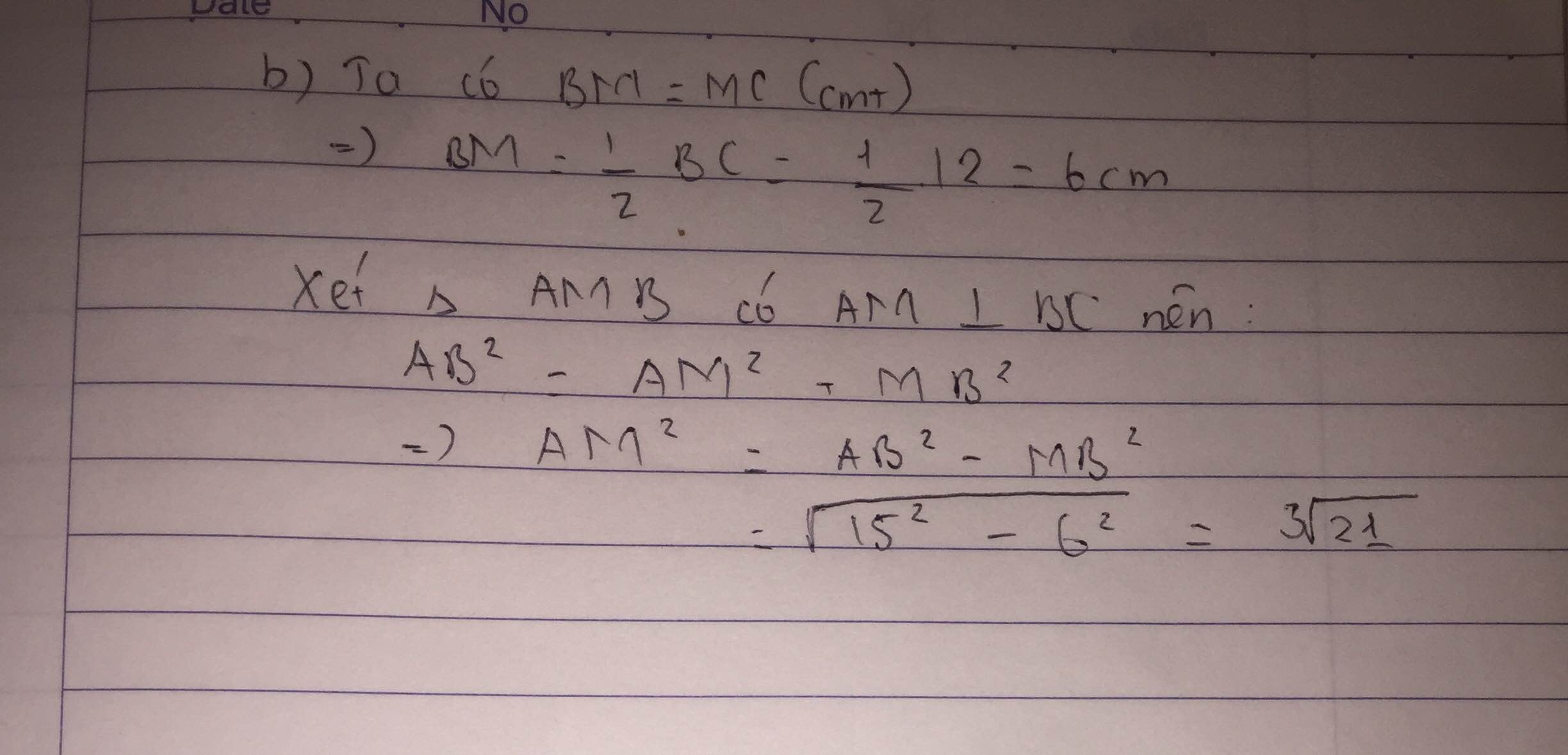Từ M kẻ \(MH\perp AC\) (H thuộc AC) ta có

\(MH\perp AC\) 

\(AB\perp AC\)

=> MH//AB (cùng vuông góc với AC) (1)

BM=CM (2)

=> AH=CH (trong tam giác đường thẳng // với 1 cạnh và đi qua trung điểm của 1 cạnh thì đi qua trung điểm cạnh còn lại)

Trong ta giác AMC có

\(MH\perp AC;AH=HC\) => tam giác AMC cân tại M (ta giác có đường cao đồng thời là đường trung tuyến thì tg đó là tg cân)

=> AM=CM mà CM=BM => AM=BM=CM \(\Rightarrow AM=\frac{1}{2}BC\)

câu 2 : 

a) có phải là chứng minh AM ⊥ BC không

xét ΔAMB và ΔAMC, ta có : 

AB = AC (2 cạnh bên của ΔABC cân tại A)

MB = MC (AM là đường trung tuyến của cạnh BC)

AM là cạnh chung

=> ΔAMB = ΔAMC (c.c.c)

=> \(\widehat{AMB}=\widehat{AMC}\) (2 cạnh tương ứng)

mà \(\widehat{AMB}+\widehat{AMC}=180^O\) (kề bù)

\(\Rightarrow\widehat{AMB}=\widehat{AMC}=\dfrac{180^O}{2}=90^O\)

=> AM ⊥ BC

a) Xét ΔABM và ΔDCM có:

       BM=MC(gt)

      \(\widehat{BMA}=\widehat{CMD}\)(đđ)

      AM=DM

=> ΔABM=ΔDCM(c.g.c)

=>\(\widehat{ABM}=\widehat{MCD}\) .Mà 2 góc này ở vị trí soletrong)

=>AB//CD

b)Vì ΔABC vuông tại A(gt)

=> AM=BM=MC

 Có: AD=AM+MD

          BC=MB+MC

Mà: AM=BM(cmt); MD=MC(cmt)

=>BC=AM

Vì ΔABM=ΔDCM(cmt)

=>AB=DC

Xét ΔABC và ΔCDA có:

      AB=DC(cmt)

     AC: cạnh chung

       BC=AD(cmt)

=>ΔABC=ΔCDM(c.c.c)

c) Vì ΔABC vuông tại A(gt)

=>AM=BC/2

1) Xét tam giác ABM và tam giác DCM có:

BM=MC (vì M là trung điểm của BC)

góc BMA=góc CMD (hai góc đối đỉnh)

MA=MD (gt)

=> tam giác ABM=tam giác DCM (c.g.c)

=> góc ABM=góc DCM

Mà góc ABM và góc DCM là 2 góc so le trong nên AB//CD

2) Vì CD//AB mà AB vuông góc với AC nên CD vuông góc góc AC

=> góc ACD=90 độ

Theo câu 1): tam giác ABM=tam giác CDM

=> AB=CD

Xét tam giác ABC và tam giác CDA có:

AB=CD (cmt)

góc BAC=góc DCA=90 độ

AC:chung

=> tam giác ABC=tam giác CDA (c.g.c)

3) Theo 2) tam giác ABC=tam giác CDA

=> BC=DA

Mà AM=\(\frac{1}{2}\)AD nên AM=\(\frac{1}{2}BC\)

a: Xét ΔABM và ΔACM có

AB=AC

BM=CM

AM chung

=>ΔABM=ΔACM

=>góc BAM=góc CAM

=>AM là phân giác của góc BAC

b: ΔABC cân tại A 

mà AM là trung tuyến

nên AM vuông gócBC

a: Xét ΔABM và ΔACM có

AB=AC

BM=CM

AM chung

=>ΔABM=ΔACM

=>góc BAM=góc CAM

=>AM là phân giác của góc BAC

b: ΔABC cân tại A 

mà AM là trung tuyến

nên AM vuông gócBC

Trên tia đối của tia MA lấy D s/c MA=MD từ đó chứng minh được:

  \(\text{△AMB=△DMC(c.g.c)}\)  \(\text{⇒}\)  \(\widehat{ABM}=\widehat{DCM}\) \(mà\) \(\widehat{ABM}+\widehat{ACM}=90^O\text{ }\text{⇒}\widehat{ACD}=90^O\)

⇒ \(\text{△}ABC=\text{△}CDA\left(c.g.c\right)\) ⇒ BC=AD ⇒ \(\dfrac{1}{2}BC=\dfrac{1}{2}AD\text{⇒ }\dfrac{1}{2}BC=AM\)

vì AM là trung tuyến TG ABC => M là trung điểm BC