Giúp mình câu 37 với. Xin cảm ơn

Những câu hỏi liên quan
giúp mình 2 câu này với mình cảm xin cảm ơn
có ai giúp mình câu này với mai phải nộp rồi
Đúng 0
Bình luận (0)
Giải và vẽ hình câu 37 giúp mình với ạ..Mình cảm ơn

Không ai vẽ hình khi làm bài mặt cầu Oxyz đâu bạn, chỉ cần đại số hóa nó là được.
Gọi I là tâm mặt cầu, do mặt cầu tiếp xúc (Q) tại H nên \(IH\perp\left(Q\right)\)
\(\Rightarrow\) Đường thẳng IH nhận vtpt của (Q) là 1 vtcp
\(\Rightarrow\) IH nhận (1;1;-1) là 1 vtcp
Phương trình IH: \(\left\{{}\begin{matrix}x=1+t\\y=-1+t\\z=-t\end{matrix}\right.\)
I vừa thuộc IH vừa thuộc (P) nên là giao điểm của IH và (P)
\(\Rightarrow\) Tọa độ I thỏa mãn:
\(2\left(1+t\right)+\left(-1+t\right)+\left(-t\right)-3=0\)
\(\Rightarrow t=1\Rightarrow I\left(2;0;-1\right)\)
\(\Rightarrow\overrightarrow{IH}=\left(-1;-1;1\right)\Rightarrow R=IH=\sqrt{3}\)
Phương trình (S):
\(\left(x-2\right)^2+y^2+\left(z+1\right)^2=3\)
Đúng 1
Bình luận (0)
Giúp mình câu 42 với. Xin cảm ơn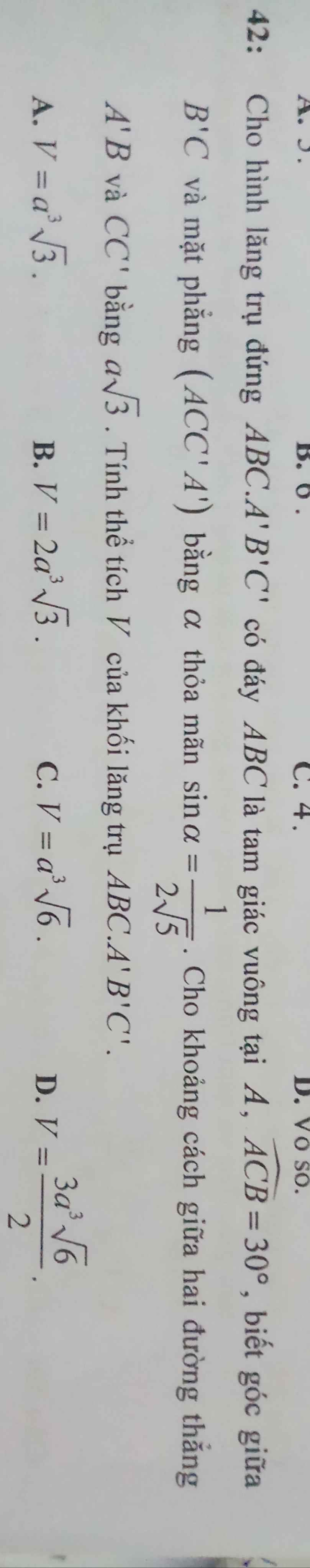
\(\left\{{}\begin{matrix}A'B'\perp AA'\\A'B'\perp A'C'\end{matrix}\right.\) \(\Rightarrow A'B'\perp\left(ACC'A'\right)\)
\(\Rightarrow\widehat{B'CA'}\) là góc giữa \(B'C\) và (ACC'A') \(\Rightarrow sin\widehat{B'CA'}=\dfrac{A'B'}{B'C}=\dfrac{1}{2\sqrt{5}}\)
Mặt khác:
\(CC'||AA'\Rightarrow CC'||\left(ABB'A'\right)\Rightarrow d\left(A'B;CC'\right)=d\left(CC';\left(ABB'A'\right)\right)=d\left(C;\left(ABB'A'\right)\right)=AC\)
\(\Rightarrow AC=a\sqrt{3}\Rightarrow AB=AC.tan30^0=a\)
\(\Rightarrow B'C=2\sqrt{5}A'B'=2a\sqrt{5}\) ; \(BC=\dfrac{AB}{sin30^0}=2a\)
\(\Rightarrow BB'=\sqrt{B'C^2-BC^2}=4a\)
\(V=\dfrac{1}{2}AB.AC.BB'=2a^3\sqrt{3}\)
Đúng 1
Bình luận (0)
Giúp mình câu này với Xin cảm ơn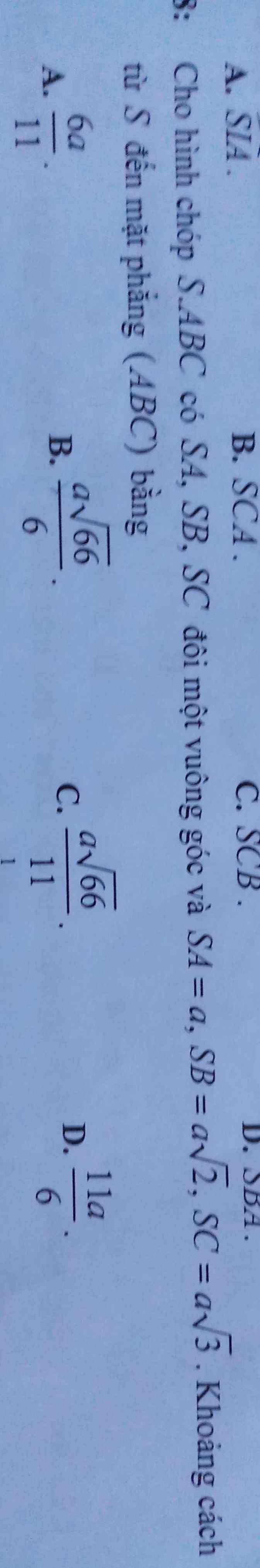
Từ S kẻ \(SH\perp AC\) (1)
Ta có: \(\left\{{}\begin{matrix}SB\perp SA\\SB\perp SC\end{matrix}\right.\) \(\Rightarrow SB\perp\left(SAC\right)\Rightarrow SB\perp AC\) (2)
(1);(2) \(\Rightarrow AC\perp\left(SBH\right)\)
Trong mp (SBH), từ S kẻ \(SK\perp BH\Rightarrow SK\perp\left(ABC\right)\)
\(\Rightarrow SK=d\left(S;\left(ABC\right)\right)\)
\(\dfrac{1}{SH^2}=\dfrac{1}{SA^2}+\dfrac{1}{SC^2}\Rightarrow SH=\dfrac{SA.AC}{\sqrt{SA^2+SC^2}}=\dfrac{a\sqrt{3}}{2}\)
\(\dfrac{1}{SK^2}=\dfrac{1}{SB^2}+\dfrac{1}{SH^2}\Rightarrow SK=\dfrac{SB.SH}{\sqrt{SB^2+SH^2}}=\dfrac{a\sqrt{66}}{11}\)
Đúng 1
Bình luận (0)
Giúp mình câu này với Xin cảm ơn
\(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\) (1)
Trong mp đáy, kẻ \(AH\perp BC\) (2)
(1);(2) \(\Rightarrow BC\perp\left(SAH\right)\)
Trong mp (SAH), kẻ \(AK\perp SH\Rightarrow AK\perp\left(SBC\right)\)
Hệ thức lượng tam giác vuông ABC: \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Rightarrow AH=\dfrac{AB.AC}{\sqrt{AB^2+AC^2}}=\dfrac{a\sqrt{3}}{2}\)
Hệ thức lượng tam giác vuông SAH:
\(\dfrac{1}{AK^2}=\dfrac{1}{AH^2}+\dfrac{1}{SA^2}\Rightarrow AK=\dfrac{AH.SA}{\sqrt{AH^2+SA^2}}=\dfrac{2a\sqrt[]{57}}{19}\)
Đúng 1
Bình luận (0)
Giúp mình câu này với Xin cảm ơn
Cái chức năng xoay ảnh như bù nhìn vậy :v
Nguyên hoá \(\left(0,48;0,56;0,72\right)=\left(48;56;72\right)\Rightarrow BCNN\left(48;56;72\right)=1008\)
\(\Rightarrow\) 3 bậc trùng tại:\(\left\{{}\begin{matrix}\lambda_1:\dfrac{1008}{48}=21\Rightarrow so-van-sang-bac-1:k_1=21-1=20\\\lambda_2:\dfrac{1008}{56}=18\Rightarrow k_2=18-1=17\\\lambda_3=\dfrac{1008}{72}=14\Rightarrow k_3=14-1=13\end{matrix}\right.\)
\(\lambda_1\equiv\lambda_2:\dfrac{k_1}{k_2}=\dfrac{\lambda_2}{\lambda_1}=\dfrac{7}{6}=\dfrac{14}{12}=\dfrac{21}{18}\Rightarrow\) 2 vân bước sóng 1 trùng vơi bước sóng 2
\(\lambda_2\equiv\lambda_3:\dfrac{k_2}{k_3}=\dfrac{\lambda_3}{\lambda_2}=\dfrac{9}{7}=\dfrac{18}{14}\Rightarrow\) 1 vân bước sóng 2 trùng với bước sóng 3
\(\lambda_1\equiv\lambda_3:\dfrac{k_1}{k_3}=\dfrac{\lambda_3}{\lambda_1}=\dfrac{3}{2}=\dfrac{6}{4}=\dfrac{9}{6}=\dfrac{12}{8}=\dfrac{15}{10}=\dfrac{18}{12}=\dfrac{21}{14}\Rightarrow\) 6 vân bước sóng 1 trùng với bước sóng 3
\(\Rightarrow van-sang:k_1+k_2+k_3-6-1-2=41\left(van\right)\)
Đúng 2
Bình luận (0)
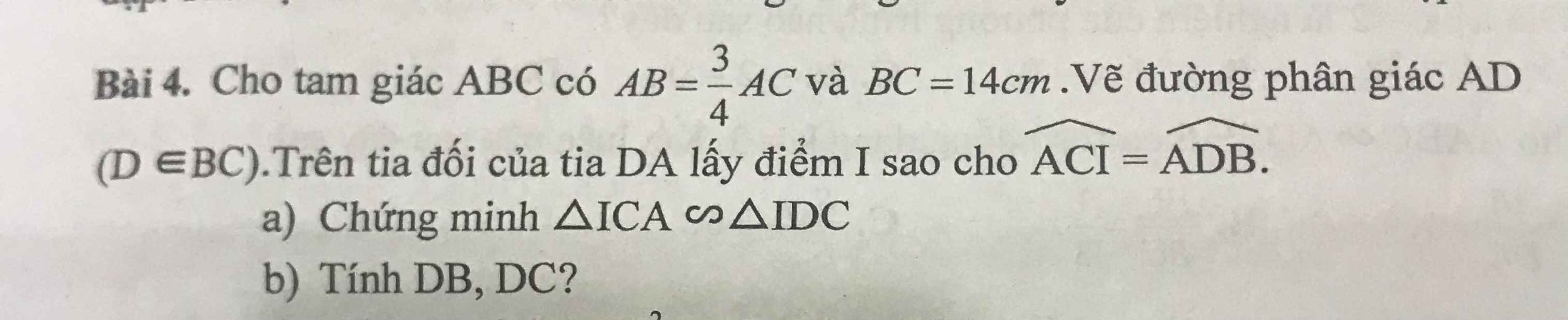
Làm giúp mình câu b với ạ. Mình xin cảm ơn
b: AD là phân giác
=>DB/AB=DC/AC
=>DB/DC=AB/AC=3/4
=>DB/3=DC/4
mà DB+DC=BC=14
nên DB/3=DC/4=14/7=2
=>DB=6cm; DC=8cm
Đúng 0
Bình luận (0)
Mọi người giúp mình câu này với ạ! Mình xin cảm ơn
Đọc tiếp
Mọi người giúp mình câu này với ạ! Mình xin cảm ơn
Hàm bậc 2 có \(\left\{{}\begin{matrix}a=1>0\\-\dfrac{b}{2a}=6-m\end{matrix}\right.\) nên nghịch biến trên khoảng \(\left(-\infty;6-m\right)\)
Hàm nghịch biến trên khoảng đã cho khi:
\(6-m\ge2\Rightarrow m\le4\)
\(\Rightarrow\) Có 4 giá trị nguyên dương của m
Đúng 1
Bình luận (0)
Giúp mình câu này với ạ,xin cảm ơn nhièu
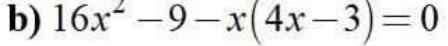
\(\Leftrightarrow\left(4x-3\right)\left(4x+3-x\right)=0\)
=>(4x-3)(3x+3)=0
=>x=3/4 hoặc x=-1
Đúng 3
Bình luận (0)














