Quy đồng mẫu thức thành 2 phân thức sau: a) x phần x3-1 và 1+x phần 1-x

Những câu hỏi liên quan
Cho hai phân thức
1
x
2
+
ax
−
2
và
2
x
2
+
4
x
−
b
, với
x
≠
−
3
;
x
≠
−
1...
Đọc tiếp
Cho hai phân thức 1 x 2 + ax − 2 và 2 x 2 + 4 x − b , với x ≠ − 3 ; x ≠ − 1 và x ≠ 2 .
a) Hãy xác định a và b biết rằng khi quy đồng mẫu thức chúng trở thành những phân thức có mẫu thức chung là A = x 3 + 2 x 2 − 5 x − 6 ;
b) Với a và b tìm được hãy viết hai phân thức đã cho và hai phân thức thu được sau khi quy đồng với mẫu thức chung là A = x 3 + 2 x 2 − 5 x − 6 .
Cho hai phân thức
1
x
2
+
a
x
-
2
và
2
x
2
+
5
x
+
b
. Hãy xác định a và b biết rằng khi quy đồng mẫu thức chúng trở thành những phâ...
Đọc tiếp
Cho hai phân thức 1 x 2 + a x - 2 và 2 x 2 + 5 x + b . Hãy xác định a và b biết rằng khi quy đồng mẫu thức chúng trở thành những phân thức có mẫu thức chung là x 3 + 4 x 2 + x - 6 . Viết tường minh hai phân thức đã cho và hai phân thức thu được sau khi quy đồng với mẫu thức chung là x 3 + 4 x 2 + x - 6
Ta có mẫu thức chung phải chia hết cho từng mẫu thức riêng.
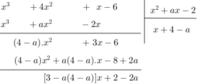
Vì phép chia này là phép chia hết nên số dư phải bằng 0, tức là:
3 – a(4 – a) = 0 và 2 – 2a = 0 ⇒ a = 1.
Vậy phân thức thứ nhất là 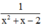
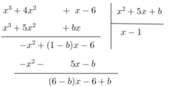
Vì phép chia này là phép chia hết nên số dư phải bằng 0, tức là:
6 – b = 0 và -6 + b = 0 ⇒ b = 6.
Vậy phân thức thứ hai là 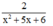
* Quy đồng:
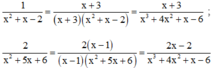
Đúng 0
Bình luận (0)
cho hai phân thức 1/x-a và 2/x-b với a<b
a) hãy xác định a và b biết rằng khi quy đồng mẫu thức chúng trở thanh những phân thức có mẫu thức chung là x^2-5x+6
b)Với a và b tìm được hãy viết hai phân thức đã cho và hai phân thức thu được sau khi quy đồng với mẫu thức chung là x2-5x+6
a) \(\dfrac{1}{x-a};\dfrac{2}{x-b}\)
Theo đề bài ta có :
\(\left(x-a\right)\left(x-b\right)=x^2-5x+6\)
\(\Leftrightarrow\left(x-a\right)\left(x-b\right)=\left(x-2\right)\left(x-3\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=3\end{matrix}\right.\)
b) \(\dfrac{1}{x-a}=\dfrac{1}{x-2}=\dfrac{x-3}{\left(x-2\right)\left(x-3\right)}=\dfrac{x-3}{x^2-5x+6}\)
\(\dfrac{2}{x-b}=\dfrac{1}{x-3}=\dfrac{2\left(x-2\right)}{\left(x-2\right)\left(x-3\right)}=\dfrac{2x-6}{x^2-5x+6}\)
Đúng 0
Bình luận (0)
Quy đồng mẫu các phân thức sau:
a) 1 phần x+2 và 8 phần 2x-x2
b) x2+1 và x2 phần x2-1
a)
\(\dfrac{1}{x+2}=\dfrac{1}{2+x}\)
\(\dfrac{8}{2x-x^2}=\dfrac{-8}{-x\left(2+x\right)}=\dfrac{8}{x\left(2+x\right)}\)
MTC: \(x\left(2+x\right)\)
\(\dfrac{1}{x+2}=\dfrac{1}{2+x}=\dfrac{x}{x\left(2+x\right)}\)
\(\dfrac{8}{2x-x^2}=\dfrac{-8}{-x\left(2+x\right)}=\dfrac{8}{x\left(2+x\right)}\)
Đúng 0
Bình luận (0)
b)
\(x^2+1=\dfrac{x^2+1}{1}\)
\(\dfrac{x^2}{x^2-1}=\dfrac{x^2}{\left(x-1\right)\left(x+1\right)}\)
MTC: \(\left(x-1\right)\left(x+1\right)\)
\(x^2+1=\dfrac{x^2+1}{1}=\dfrac{\left(x-1\right)\left(x+1\right)\left(x^2+1\right)}{\left(x-1\right)\left(x+1\right)}\)
\(\dfrac{x^2}{x^2-1}=\dfrac{x^2}{\left(x-1\right)\left(x+1\right)}\)
Đúng 0
Bình luận (0)
Quy đồng mẫu thức hai phân thức
4 phần x+2 và 2-x phần 3(x bình +4x+4)
\(\frac{4}{x+2}\)và \(\frac{2-x}{x^2+4x+4}\)
Ta có : \(x^2+4x+4=\left(x+2\right)^2\)
\(\Rightarrow\text{MTC}=\left(x+2\right)^2\)
\(\Rightarrow\hept{\begin{cases}\frac{4}{x+2}=\frac{4\left(x+2\right)}{\left(x+2\right)\left(x+2\right)}=\frac{4x+8}{\left(x+2\right)^2}\\\frac{2-x}{x^2+4x+4}=\frac{2-x}{\left(x+2\right)^2}\end{cases}}\)
Đúng 0
Bình luận (0)
Quy đồng mẫu thức các phân thức sau: a) 1/x^2y và 3/xy b) x/(x^2+2xy+y^2) và 2x/(x^2+xy)
a: 1/x^2y=1/x^2y
3/xy=3x/x^2y
b: \(\dfrac{x}{x^2+2xy+y^2}=\dfrac{x}{\left(x+y\right)^2}\)
\(\dfrac{2x}{x^2+xy}=\dfrac{2}{x+y}=\dfrac{2x+2y}{\left(x+y\right)^2}\)
Đúng 2
Bình luận (1)
bài 6 quy dồng mẫu thức các phân tử a)1 phần x+1 và 6 phần x-x mũ 2 với x khác 0 và x khác - hoặc + 1 b) y+5 phần y mũ 2 +8y +16 và y phần 3 y+12 với y khác -4
quy đồng các mẫu thức sau
a 1 / x3-8 và 3 / 4-2x
b x / x2-1 và 1 / x2+2x+1
c 1 / x+2 ; x+1 / x2-4x-4 và 5 / 2-x
d 1 / 3x+3y;2x / x2-y2 và x2-xy+y2 / x2-2xy+y2
a) \(\dfrac{1}{x^3-8}=\dfrac{1}{\left(x-2\right)\left(x^2+2x+4\right)}=\dfrac{2}{2\left(x-2\right)\left(x^2+2x+4\right)}\)
\(\dfrac{3}{4-2x}=\dfrac{-3}{2\left(x-2\right)}=\dfrac{-3\left(x^2+2x+4\right)}{2\left(x-2\right)\left(x^2+2x+4\right)}\)
b) \(\dfrac{x}{x^2-1}=\dfrac{x}{\left(x+1\right)\left(x-1\right)}=\dfrac{x\left(x+1\right)}{\left(x+1\right)^2\left(x-1\right)}\)
\(\dfrac{1}{x^2+2x+1}=\dfrac{1}{\left(x+1\right)^2}=\dfrac{x-1}{\left(x+1\right)^2\left(x-1\right)}\)
c) \(\dfrac{1}{x+2}=\dfrac{\left(x-2\right)^2}{\left(x+2\right)\left(x-2\right)^2}\)
\(\dfrac{1}{x^2-4x+4}=\dfrac{1}{\left(x-2\right)^2}=\dfrac{x+2}{\left(x+2\right)\left(x-2\right)^2}\)
\(\dfrac{5}{2-x}=\dfrac{-5}{x-2}=\dfrac{-5\left(x+2\right)\left(x-2\right)}{\left(x+2\right)\left(x-2\right)^2}\)
d) \(\dfrac{1}{3x+3y}=\dfrac{1}{3\left(x+y\right)}=\dfrac{\left(x-y\right)^2}{3\left(x+y\right)\left(x-y\right)^2}\)
\(\dfrac{2x}{x^2-y^2}=\dfrac{2x}{\left(x+y\right)\left(x-y\right)}=\dfrac{6x\left(x-y\right)}{3\left(x+y\right)\left(x-y\right)^2}\)
\(\dfrac{x^2-xy+y^2}{x^2-2xy+y^2}=\dfrac{x^2-xy+y^2}{\left(x-y\right)^2}=\dfrac{3\left(x^2-xy+y^2\right)\left(x+y\right)}{3\left(x+y\right)\left(x-y\right)^2}=\dfrac{3\left(x^3+y^3\right)}{3\left(x+y\right)\left(x-y\right)^2}\)
Đúng 0
Bình luận (2)
Cho hai phân thức \(\frac{1}{x^2+ax-2}\)và \(\frac{x}{x^2+5x+b}\). Hãy xác định a và b biết rằng khi quy đồng mẫu thức chúng trở thành những phân thức có mẫu thức chung là \(x^3+4x^2+x-6\). Viết tường minh hai phân thức đã cho và hai phân thức thu được sau khi quy đồng với mẫu thức chung là \(x^3+4x^2+x-6\)
Cho hai phân thức :
dfrac{1}{x^2+ax-2} và dfrac{2}{x^2+5x+b}
Hãy xác định a và b biết rằng khi quy đồng mẫu thức chúng trở thành những phân thức có mẫu thức chung là x^3+4x^2+x-6
Viết tường minh hai phân thức đã cho và hai phân thức thu được sau khi quy đồng với mẫu thức chung là x^3+4x^2+x-6
Đọc tiếp
Cho hai phân thức :
\(\dfrac{1}{x^2+ax-2}\) và \(\dfrac{2}{x^2+5x+b}\)
Hãy xác định a và b biết rằng khi quy đồng mẫu thức chúng trở thành những phân thức có mẫu thức chung là \(x^3+4x^2+x-6\)
Viết tường minh hai phân thức đã cho và hai phân thức thu được sau khi quy đồng với mẫu thức chung là \(x^3+4x^2+x-6\)
























