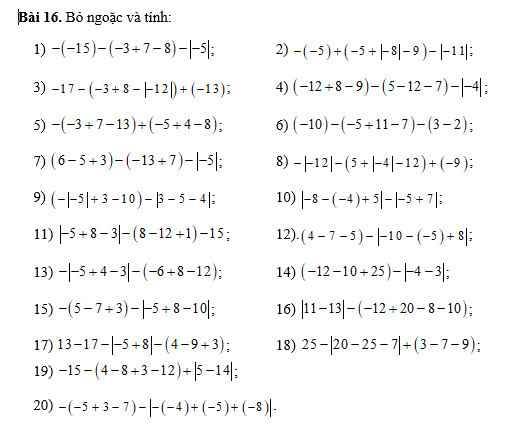 cho em một lời giải rõ ràng, cảm ơn ạ!
cho em một lời giải rõ ràng, cảm ơn ạ!

Những câu hỏi liên quan
Giải thích rõ ràng hộ em với (làm thành bài ạ). Em cảm ơn

Câu 12.
\(5\sqrt{a}+6\sqrt{\dfrac{a}{4}}-a\sqrt{\dfrac{4}{a}}+5\sqrt{\dfrac{4a}{25}}\)
\(=5\sqrt{a}+6\dfrac{\sqrt{a}}{2}-a\cdot\dfrac{2}{\sqrt{a}}+5\dfrac{2\sqrt{a}}{5}\)
\(=5\sqrt{a}+3\sqrt{a}-2\sqrt{a}+2\sqrt{a}\) (vì a>0)
\(=8\sqrt{a}\)
Đúng 1
Bình luận (0)
Câu 13. Chọn C.
Do x,y\(\ge\)0, x\(\ne\)y ta có:
\(A=\dfrac{x-\sqrt{xy}}{x-y}=\dfrac{\sqrt{x}\left(\sqrt{x}-\sqrt{y}\right)}{\left(\sqrt{x}-\sqrt{y}\right)\cdot\left(\sqrt{x}+\sqrt{y}\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}+\sqrt{y}}\)
Đúng 1
Bình luận (0)
Nhờ mn giúp em với ạ, mn xem em làm bài đúng ko ạ?
Đúng 0
Bình luận (0)

Mọi người giải giúp em với ạ, mai em thi rồi, mấy anh/chị giải thích rõ ràng giùm em nhé, em cảm ơn ạ.
Bài `13`
\(a,\sqrt{27}+\sqrt{48}-\sqrt{108}-\sqrt{12}\\ =\sqrt{9\cdot3}+\sqrt{16\cdot3}-\sqrt{36\cdot3}-\sqrt{4\cdot3}\\ =3\sqrt{3}+4\sqrt{3}-6\sqrt{3}-2\sqrt{3}\\ =\left(3+4-6-2\right)\sqrt{3}\\ =-\sqrt{3}\\ b,\left(\sqrt{28}+\sqrt{12}-\sqrt{7}\right)\cdot\sqrt{7}+\sqrt{84}\\ =\left(\sqrt{4\cdot7}+\sqrt{4\cdot3}-\sqrt{7}\right)\cdot\sqrt{7}+\sqrt{4\cdot21}\\ =\left(2\sqrt{7}+2\sqrt{3}-\sqrt{7}\right)\cdot\sqrt{7}+2\sqrt{21}\\ =2\cdot7+2\sqrt{21}-7+2\sqrt{21}\\ =14+2\sqrt{21}-7+2\sqrt{21}\\ =7+4\sqrt{21}\)
Đúng 0
Bình luận (1)
17:
ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x< >4\end{matrix}\right.\)
Để A là số nguyên thì \(\sqrt{x}-1⋮\sqrt{x}-2\)
=>\(\sqrt{x}-2+1⋮\sqrt{x}-2\)
=>\(\sqrt{x}-2\in\left\{1;-1\right\}\)
=>\(\sqrt{x}\in\left\{3;1\right\}\)
=>\(x\in\left\{9;1\right\}\)
16:
a: BC=BH+CH
=9+16
=25(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH=\sqrt{9\cdot16}=12\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=\sqrt{9\cdot25}=15\left(cm\right)\\AC=\sqrt{16\cdot25}=20\left(cm\right)\end{matrix}\right.\)
b: M là trung điểm của AC
=>AM=AC/2=10(cm)
Xét ΔAMB vuông tại A có
\(tanAMB=\dfrac{AB}{AM}=\dfrac{15}{10}=\dfrac{3}{2}\)
nên \(\widehat{AMB}\simeq56^0\)
Đúng 0
Bình luận (0)
GIẢI GIÚP EM CÂU 5 TRÌNH BÀY RÕ RÀNG DỄ HIẾU VỚI Ạ , EM CẢM ƠN 
Câu 5:
a: Xét tứ giác AHMK có
\(\widehat{AHM}=\widehat{AKM}=\widehat{KAH}=90^0\)
Do đó: AHMK là hình chữ nhật
Đúng 0
Bình luận (0)
Làm rõ ràng hộ em ạ, cảm ơn ạ <3
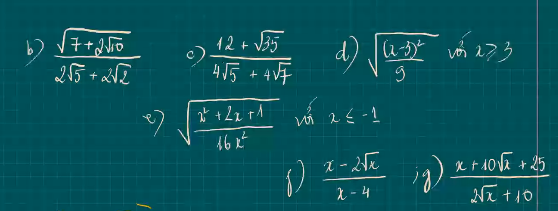
Làm rõ ràng hộ em ạ, em cảm ơn <3
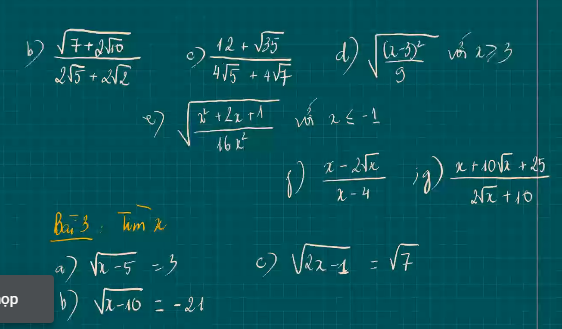
a) \(\sqrt{x-5}=3\)
\(x-5=9\)
\(x=14\)
b) Vì \(\sqrt{x-10}\) ≥0
⇒không có x thỏa mãn
c) \(\sqrt{2x-1}=\sqrt{7}\)
\(2x-1=7\)
\(2x=8\)
\(x=4\)
Đúng 1
Bình luận (0)
Bài 3
a) \(\sqrt{x-5}=3\)
\(\Rightarrow x-5=9\)
\(\Rightarrow x=14\)
b) \(\sqrt{x-10}=-21\)
\(\Rightarrow x\in\varnothing\)
c) \(\sqrt{2x-1}=\sqrt{7}\)
\(\Rightarrow2x-1=7\)
\(\Rightarrow2x=8\)
\(\Rightarrow x=4\)
Đúng 1
Bình luận (0)
Tìm một số, biết số đó chia cho 7 được 8 và có số dư lớn nhất. Cho mình xin lời giải rõ ràng với nhé. Cảm ơn nhìu!!!
Số dư lớn nhất là : 6
Muốn tìm số bị chia ta lấy số chia nhân thương rồi cộng với số dư.
SỐ đó là: (7 x 8 ) + 6 = 62 .
Đáp số : 62
Đúng 0
Bình luận (0)
Số dư lớn nhất có thể là : 6
Số đó là :
7 x 8 + 6 = 62
Đúng 0
Bình luận (0)
Số dư luôn bé hơn số chia nên số dư lớn nhất là : 7-1=6
Số cần tìm là:
8 x 7 + 6= 62
ĐS: 62
Vậy rõ chưa bạn??
Đúng 0
Bình luận (0)
Xem thêm câu trả lời

giải, trình bày rõ ràng đầy đủ và vẽ hình giúp mình với ạ mình cảm ơn
Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)
Đúng 0
Bình luận (0)
Câu lúc nãy mình gửi trước 4 giờ nhé . Được không ạ . Mình cảm ơn trước , cảm ơn chân thành . giải rõ ràng nhé .
Lúc 6 giờ 15 phút một xe gắn máy đi từ A đến B với vận tốc 32km/giờ.Sau đó đi đến 8 giờ 30 phút một ô tô cũng xuất phát từ A đến B với vận tốc bằng 5/4 vận tốc của xe máy. Hỏi sau bao lâu ô tô đuổi kịp xe máy?
Lời giải đáp số rõ ràng giúp em với ạ. Em cảm ơn.
Trình bày cách giải rõ ràng, ct, đơn vị đầy đủ cho e vs ạ tại cô bắt có đầy đủ😅e cảm ơn mn
3.
\(F=\dfrac{k.\left|q_1.q_2\right|}{r^2}=\dfrac{9.10^9.\left|9.10^{-18}\right|}{0,1^2}=8,1.10^{-6}N\)
Đúng 1
Bình luận (0)
1.
\(F=\dfrac{k.\left|q_1.q_2\right|}{r^2}=\dfrac{9.10^9.\left|5.10^8.\left(-1,6.10^{-19}\right).5.10^8.\left(-1,6.10^{-19}\right)\right|}{0,02^2}=1,44.10^{-7}N\)
Đúng 0
Bình luận (0)























