Cho m, n là các số nguyên. CMR:
a) ab(a2+2)(2b2+1)⋮9
b) mn(m2-n2)(4m2-n2)⋮10
Những câu hỏi liên quan
1.Cho a,b,c là các số nguyên tố thoả mãn: ab + 1 = c. CMR: a2+ c hoặc b2+ c là số chính phương
2.Cho m,n là các số nguyên dương thoả mãn: m2+n2+m⋮mn. CMR: m là một số chính phương
Bài 1 : Phân tích các đa thức sau thành nhân tửa) m3p + m2np - m2p2 - mnp2 b) ab( m2 + n2 ) + mn( a2 + b2 )Bài 2 : Phân tích các đa thức sau thành nhân tử a) (xy + ab )2 + ( ay - bx )2b) m2( n - p ) + n2( p - m ) + p2?( m - n )Bài 3 : Tìm y để giá trị của biểu thức 1 + 4y - y2 là lớn nhấtBài 4 : Tìm x , biết : ( x3 - x2 ) - 4x2 + 8x - 4 0Bài 5 : Phân tích đa thức sau thành nhân tử A ( a + b + c )3 - ( a + b - c )3 - ( b + c - a )3 - ( c + a - b )3
Đọc tiếp
Bài 1 : Phân tích các đa thức sau thành nhân tử
a) m3p + m2np - m2p2 - mnp2
b) ab( m2 + n2 ) + mn( a2 + b2 )
Bài 2 : Phân tích các đa thức sau thành nhân tử
a) (xy + ab )2 + ( ay - bx )2
b) m2( n - p ) + n2( p - m ) + p2?( m - n )
Bài 3 : Tìm y để giá trị của biểu thức 1 + 4y - y2 là lớn nhất
Bài 4 : Tìm x , biết : ( x3 - x2 ) - 4x2 + 8x - 4 = 0
Bài 5 : Phân tích đa thức sau thành nhân tử
A = ( a + b + c )3 - ( a + b - c )3 - ( b + c - a )3 - ( c + a - b )3
Bài 4:
Ta có: \(\left(x^3-x^2\right)-4x^2+8x-4=0\)
\(\Leftrightarrow x^2\left(x-1\right)-4\left(x-1\right)^2=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho m, n số nguyên dương, m2 + n2 + m chia hết cho mn. CMR m là số chính phương
Cho m, u là các số nguyên dương. Tìm giá trị chỏ nhất của vdk=m2+n2+1/m2+1/n2+2014
Bài 1 : Phân tích các đa thức sau thành nhân tử
a) m3p + m2np - m2p2 - mnp2
b) ab( m2 + n2 ) + mn( a2 + b2 )
a) \(=mp\left(m^2+mn-mp-np\right)=mp\left[m\left(m+n\right)-p\left(m+n\right)\right]=mp\left(m+n\right)\left(m-p\right)\)
b) \(=abm^2+abn^2+a^2mn+b^2mn=am\left(bm+an\right)+bn\left(bm+an\right)\)
\(=\left(bm+an\right)\left(am+bn\right)\)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có AB = a, BC = b, BD = m, AC = n. Chứng minh rằng: m2 + n2 = 2(a2 + b2).
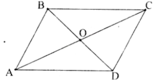
Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD.
Xét ΔABC có BO là trung tuyến
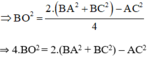
Mà O là trung điểm của BD nên BD = 2. BO ⇒ BD2 = 4. BO2
⇒ BD2 = 2.(AB2 + BC2) – AC2
⇒ BD2 + AC2 = 2.(AB2 + BC2)
⇒ m2 + n2 = 2.(a2 + b2) (ĐPCM).
Đúng 0
Bình luận (0)
“Chứng minh rằng
2
là số vô tỉ”. Một học sinh đã làm như sau: Bước 1: Giả sử
2
là số hữu tỉ, tức là
2
m
n
, trong đó m, n ∈ N* , (m, n) 1 Bước 2: Từ
2
m
n
m2 2n2 m2 là số chẵn m là số chẵn m 2k, k ∈ N*. n2 2k2 n2 là số chẵn n là số chẵn Bước 3: Do đó...
Đọc tiếp
“Chứng minh rằng 2 là số vô tỉ”. Một học sinh đã làm như sau:
Bước 1: Giả sử 2 là số hữu tỉ, tức là 2 = m n , trong đó m, n ∈ N* , (m, n) = 1
Bước 2: Từ 2 = m n => m2 = 2n2 => m2 là số chẵn
=> m là số chẵn => m = 2k, k ∈ N*.
=> n2 = 2k2 => n2 là số chẵn => n là số chẵn
Bước 3: Do đó m chẵn, n chẵn mâu thuẫn với (m, n) = 1.
Bước 4: Vậy 2 là số vô tỉ.
Lập luận trên đúng tới bước nào?
A. Bước 1.
B. Bước 2.
C. Bước 3.
D. Bước 4.
Đáp án: D
Các bước giải bài toán trên đều đúng.
Đúng 0
Bình luận (0)
Có bao nhiêu cặp số nguyên tố thứ tự (m,n), sao cho m2+2 là số nguyên tố và 2m2=n2-2
Cho hàm số
f
x
e
1
+
1
x
2
+
1
(
x
+
1
)
2
, biết rằn...
Đọc tiếp
Cho hàm số f x = e 1 + 1 x 2 + 1 ( x + 1 ) 2 , biết rằng f 1 . f 2 . f 3 . . . f 2017 = e m n với m, n là các số tự nhiên và m 2 tối giản. Tính m 2 - n 2 .
A. m 2 - n 2 = 2018
B. m 2 - n 2 = 1
C. m 2 - n 2 = - 2018
D. m 2 - n 2 = - 1
Tìm các số nguyên n sao cho:
a) n2 – 10 chia hết cho n – 1
b) n2 + 4n + 13 chia hết cho n + 2