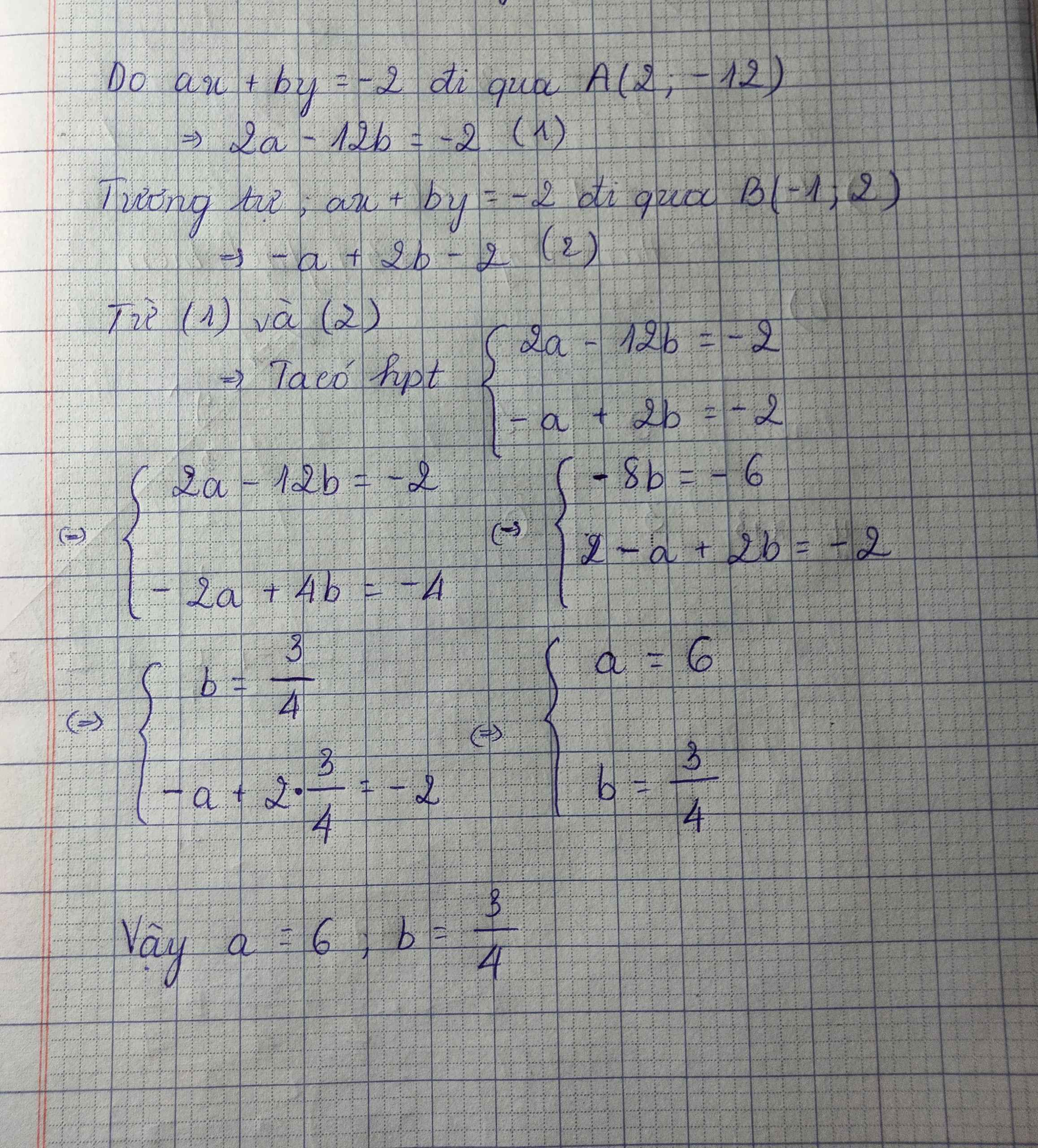Tìm a,b để đường thẳng ax+by=6 đi qua A(1;2) và N(-2;3)

Những câu hỏi liên quan
Tìm giá trị của a và b để đường thẳng ax – by = 4 đi qua hai điểm A(4; 3), B(-6; -7)
Đường thẳng ax – by = 4 đi qua hai điểm A(4; 3), B(-6; -7) nên tọa độ của A và B nghiệm đúng phương trình đường thẳng.
*Với điểm A: 4a – 3b = 4
*Với điểm B: -6a + 7b = 4
Hai số a và b là nghiệm của hệ phương trình: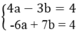
Vậy a = 4, b = 4.
Đúng 0
Bình luận (0)
Tìm các giá trị của a và b để đường thẳng ax-by=4 đi qua 2 điểm A(4:3) và B(-6:-7)
Vì đường thẳng ax-by=4 đi qua 2 điểm A(4;3) và B(-6;-7)
nên 4a-3b=4 và -6a-(-7)b=4
3(4a-3b)=12 và 2(-6a+7b)=8
12a-9b=12 và -12a+14b=8
5b=20 và 4a-3b=4
b=4 và a=4
Cho đường thẳng : y=ax+b (1)
Tìm a,b để đường thẳng (1) song song với đường thẳng y=5x+6 và đi qua điểm A(2;3)
Để đường thẳng: y=ax+b song song với đường thẳng: y=5x+6
\(\Rightarrow a=5;b\ne6\)
Vì đường thẳng: y=ax+b đi qua điểm A(2;3)
=> 2a+b=3\(\Rightarrow10+b=3\)=>b=-7(TM)
Vậy (a;b)=(5;-7)
Đúng 2
Bình luận (0)
Phần tự luận
Nội dung câu hỏi 1
a)Tìm giá trị của a và b để đường thẳng ax + by = 4 đi qua hai điểm A(4;-3) và B(-6;7).
Tìm a và b để: Đường thẳng ax – 8y = b đi qua điểm M(9; -6) và đi qua giao điểm của hai đường thẳng ( d 1 ): 2x + 5y = 17, ( d 2 ): 4x – 10y = 14.
Tọa độ giao điểm của hai đường thẳng (
d
1
): 2x + 5y = 17, (
d
2
): 4x – 10y = 14 là nghiệm của hệ phương trình: 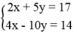
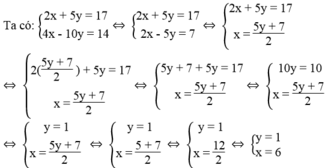
Khi đó ( d 1 ) và ( d 2 ) cắt nhau tại N(6; 1).
Đường thẳng ax – 8y = b đi qua điểm M(9; -6) và N(6;1) nên tọa độ của M và N nghiệm đúng phương trình đường thẳng.
*Điểm M: 9a + 48 = b
*Điểm N: 6a – 8 = b
Khi đó a và b là nghiệm của hệ phương trình: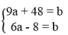
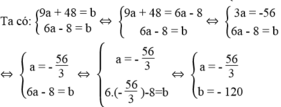
Vậy khi a = - 56/3 , b = -120 thì đường thẳng ax – 8y = b đi qua điểm M(9; -6) và đi qua giao điểm của hai đường thẳng ( d 1 ): 2x + 5y = 17, ( d 2 ): 4x – 10y = 14.
Đúng 0
Bình luận (0)
TÌM CÁC GIÁ TRỊ A,B BIẾT :
A) ax+by =1 đi qua a(-2;1)và b (3;-2)
b) đường thẳng 3ax+2by=5 đi qua m(-1;2)và vuông góc đường thẳng 2x+3y=1
Tìm hai số a và b sao cho 5a – 4b = -5 và đường thẳng: ax + by = -1 đi qua điểm A(-7; 4).
Đường thẳng ax + by = -1 đi qua điểm A(-7; 4) nên tọa độ của A nghiệm đúng phương trình đường thẳng.
Ta có: a.(-7) + b.4 = -1
Khi đó ta có phương trình: 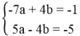
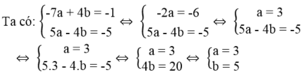
Vậy a = 3, b = 5.
Đúng 0
Bình luận (0)
tìm 2 số a và b sao cho 5a - 4b =-5 và đường thẳng ax + by =-1 đi qua điểm A(-7,4)
tìm a và b biết đường thẳng ax+by=-2 đi qua 2 điểm A(2;-12) và B(-1;2)
a) Tìm các giá trị của a và b để đường thẳng (d): yax+b đi qua hai điểm M(1;5) và N(2;8).b) Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d): y 2x – a + 1 và parabol (P): y dfrac{1}{2}x^2.1.Tìm a để đường thẳng a đi qua điểm A (-1;3)2.Tìm a để (d) cắt (P) tại hai điểm phân biệt có tọa độ (x_1;x_2) và (x_2;y_2) thỏa mãn điều kiện x_1x_2left(y_1+y_2right)+480
Đọc tiếp
a) Tìm các giá trị của a và b để đường thẳng (d): y=ax+b đi qua hai điểm M(1;5) và N(2;8).
b) Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d): y = 2x – a + 1 và parabol (P): y = \(\dfrac{1}{2}x^2\).
1.Tìm a để đường thẳng a đi qua điểm A (-1;3)
2.Tìm a để (d) cắt (P) tại hai điểm phân biệt có tọa độ (\(x_1;x_2\)) và (\(x_2;y_2\)) thỏa mãn điều kiện \(x_1x_2\left(y_1+y_2\right)+48=0\)
a: Theo đề, ta có:
\(\left\{{}\begin{matrix}a+b=5\\2a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=2\end{matrix}\right.\)
b:
1: Thay x=-1 và y=3 vào (d), ta được:
\(2\cdot\left(-1\right)-a+1=3\)
=>-a-1=3
=>-a=4
hay a=-4
Đúng 2
Bình luận (0)