cho phân thức B=x*2-8x+16/x-4
a,tìm x để B =1
b,tìm x để B=1
c, rút gọn B
Cho phân thức A= x²+8x+16/ x²-16 a) Tìm điều kiện xác định của A. b) Rút gọn phân thức. c) Tìm giá trị của x để phân thức A có giá trị bằng 3. d ) Có giá trị nào của x để giá trị của phân thức A bằng 0 hay không? Tại sao?
Lời giải:
a. ĐKXĐ: $x^2-16\neq 0\Leftrightarrow (x-4)(x+4)\neq 0$
$\Leftrightarrow x\neq \pm 4$
b. $A=\frac{x^2+8x+16}{x^2-16}=\frac{(x+4)^2}{(x-4)(x+4)}=\frac{x+4}{x-4}$
c. $A=3\Leftrightarrow \frac{x+4}{x-4}=3$
$\Rightarrow x+4=3(x-4)$
$\Leftrightarrow -2x+16=0$
$\Leftrightarrow x=8$ (tm)
d.
$A=0\Leftrightarrow \frac{x+4}{x-4}=0\Leftrightarrow x+4=0\Leftrightarrow x=-4$
Mà theo ĐKXĐ thì $x\neq \pm 4$ nên không tồn tại $x$ để $A=0$
Cho biểu thức B = \(\dfrac{x+1}{x}+\dfrac{2}{1-x}+\dfrac{3x+1}{x^2-x}\)
a) Rút gọn B
b) Tìm B biết |x| = 1
c) Tìm các giá trị nguyên của x để B nhận giá trị nguyên.
a: \(B=\dfrac{x^2-1-2x+3x+1}{x\left(x-1\right)}=\dfrac{x^2+x}{x\left(x-1\right)}=\dfrac{x+1}{x-1}\)
a) B = \(\dfrac{x+1}{x}-\dfrac{2}{x-1}+\dfrac{3x+1}{x\left(x-1\right)}\) (ĐK: \(x\ne0;1\))
= \(\dfrac{\left(x+1\right)\left(x-1\right)}{x\left(x-1\right)}-\dfrac{2x}{x\left(x-1\right)}+\dfrac{3x+1}{x\left(x-1\right)}\)
= \(\dfrac{x^2-1-2x+3x+1}{x\left(x-1\right)}=\dfrac{x^2+x}{x\left(x-1\right)}=\dfrac{x+1}{x-1}\)
b) \(\left|x\right|=1< =>\left[{}\begin{matrix}x=1\left(L\right)\\x=-1\left(C\right)\end{matrix}\right.\)
Thay x = -1 vào B, ta có:
\(\dfrac{-1+1}{-1-1}=0\)
c) B nguyên <=> \(\dfrac{x+1}{x-1}\) nguyên <=> \(1+\dfrac{2}{x-1}\) nguyên
<=> 2\(⋮x-1\)
<=> x-1 \(\in\left\{-2;-1;1;2\right\}\)
| x-1 | -2 | -1 | 1 | 2 |
| x | -1 | 0 | 2 | 3 |
| C | L | C | C |
KL: x \(\in\left\{-1;2;3\right\}\)
1 Cho biểu thức B=\(\frac{x\sqrt{x}-4x-\sqrt{x}+4}{2x\sqrt{x}-14x+28\sqrt{x}-16}\)
a) Tìm x để A có nghĩa, từ đó rút gọn biểu thức B
b) Tìm các giá trị nguyên của x để biểu thức B nhận giá trị nguyên
2 cho biểu thức P=\(\left(\frac{4\sqrt{x}}{2+\sqrt{x}}+\frac{8x}{4-x}\right)\div\left(\frac{\sqrt{x}-1}{x-2\sqrt{x}}-\frac{2}{\sqrt{x}}\right)\)
a) Rút gọn P
b) Tìm giá trị của x để P=-1
3 Rút gọn Q=\(\frac{2\sqrt{4-\sqrt{5+21+\sqrt{80}}}}{\sqrt{10}-\sqrt{2}}\)
Cho biểu thức: B=3/2x-4+7/x+2-6/x^2-4
a. Tìm điều kiện của x để B có nghĩa
b. Rút gọn biểu thức B
c. Tính giá trị của B khi x=1/4
Cho biểu thức A = \(\left(\dfrac{4x}{x+2}-\dfrac{x^3-8}{x^3+8}.\dfrac{4x^2-8x+16}{x^2-4}\right):\dfrac{16}{x^2-x-6}\)
a) Rút gọn A
b) Tìm x để A < 0
c) Tìm x để A ≥ 5
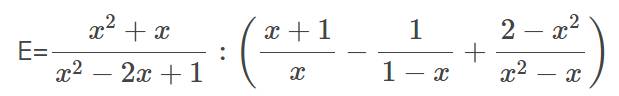
a,rút gọn
b,tìm x để E>1
c,tìm x ∈ z để E ∈ z
Đk: \(x\ne1;x\ne0\)
a) \(E=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}:\left[\dfrac{x+1}{x}+\dfrac{1}{x-1}+\dfrac{2-x^2}{x\left(x-1\right)}\right]\)
\(=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}:\dfrac{\left(x+1\right)\left(x-1\right)+x+2-x^2}{x\left(x-1\right)}\)
\(=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}.\dfrac{x\left(x-1\right)}{x+1}\)
\(=\dfrac{x^2}{x-1}\)
b) \(E>1\Leftrightarrow\dfrac{x^2}{x-1}>1\) \(\Leftrightarrow\dfrac{x^2-x+1}{x-1}>0\) \(\Leftrightarrow x-1>0\)
( do \(x^2-x+1=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall x\) )
\(\Leftrightarrow x>1\)
Vậy để E>1 thì x>1
c) \(E=\dfrac{x^2}{x-1}=\dfrac{x^2-1+1}{x-1}=\dfrac{\left(x-1\right)\left(x+1\right)+1}{x-1}=x+1+\dfrac{1}{x-1}\)
\(E\in Z\Leftrightarrow x+1+\dfrac{1}{x-1}\in Z\) mà \(x\in Z\)
\(\Rightarrow x-1\inƯ\left(1\right)=\left\{-1;1\right\}\)
\(\Leftrightarrow x=0\left(ktm\right);x=2\left(tm\right)\)
Vậy \(x=2\) thì \(E\in Z\).
\(A=\frac{x^4-16}{x^4-4x^3+8x^2-16x-16}\)
a) Tìm giá trị của x để giá trị của biểu thức A xác định
b) Rút gọn A
c) Tìm x để A có giá tri bằng 2
d) Tìm các giá trị nguyên của x để A nhận giá trị nguyên
cho phân thức B=x2-10x+25 / x2-5x
A) tìm x để B xác định và rút gọn
B) tìm x để B=2,5
C) tìm x nguyên để B có giá trị nguyên
a) B xác định khi x2-5x\(\ne0\)
<=> x(x-5)\(\ne0\Leftrightarrow\hept{\begin{cases}x\ne0\\x\ne5\end{cases}}\)
\(B=\frac{x^2-10x+25}{x^2-5x}\left(x\ne0;x\ne5\right)\)
\(=\frac{\left(x-5\right)^2}{x\left(x-5\right)}=\frac{x-5}{x}\)
b) Ta có: \(B=\frac{x-5}{x}\left(x\ne0;x\ne5\right)\)
Có 2,5=\(\frac{5}{2}\). Để B=\(\frac{5}{2}\) thì \(\frac{x-5}{x}=\frac{5}{2}\)
<=> 2x-10=5x
<=> 2x-5x=10
<=> -3x=10
<=> \(x=\frac{-10}{3}\) (tmđk)
\(c,B\in Z\Leftrightarrow\frac{x-5}{x}\in Z\)
\(\Leftrightarrow1-\frac{5}{x}\in Z\in\frac{5}{x}\in Z\)
\(\Leftrightarrow x\inƯ\left(5\right)=\left\{1;-1;5;-5\right\}\)
....
Kết hợp với ĐKXĐ thì loại giá trị x = 5 đi nha
UwU
...