Câu b, c, d ạ
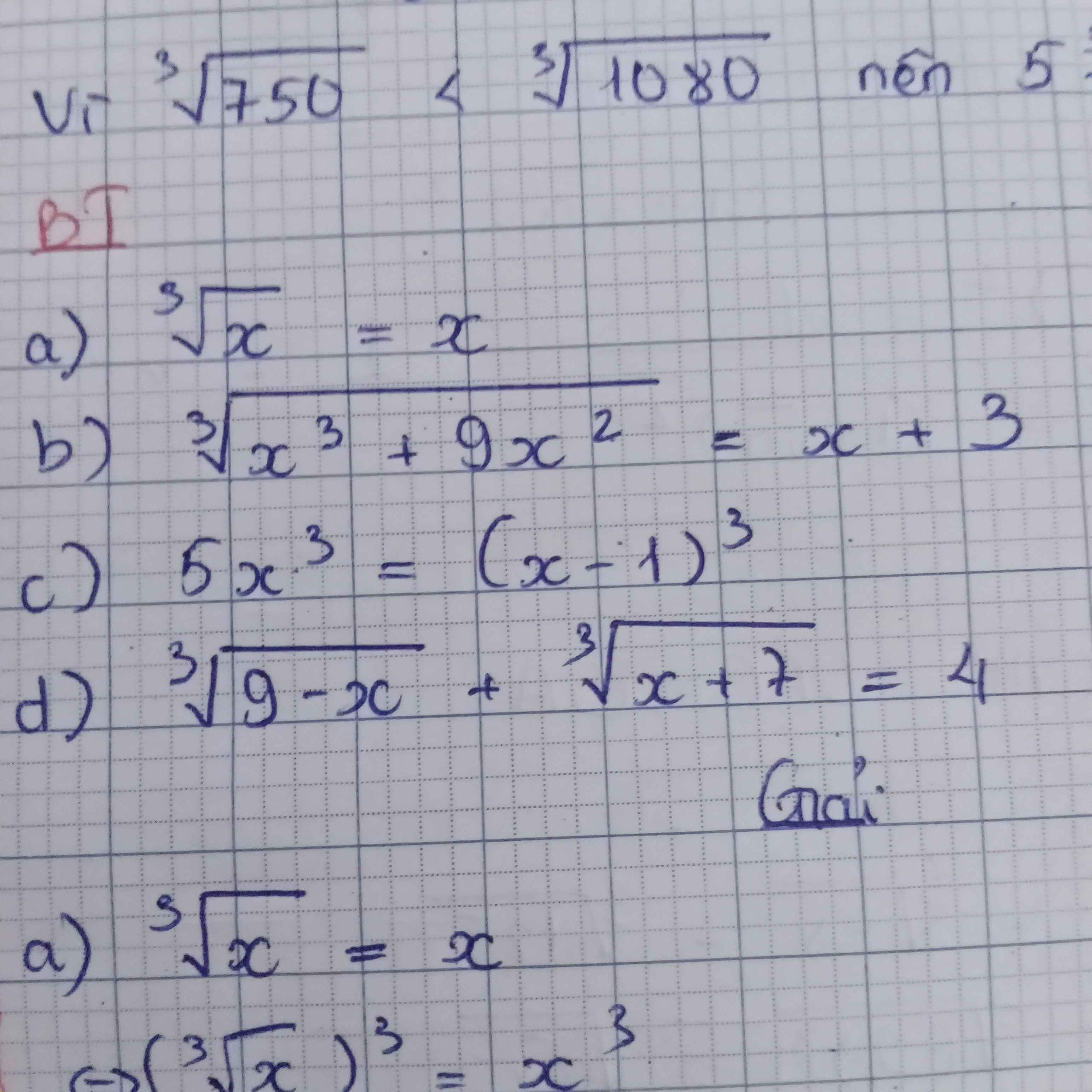
Những câu hỏi liên quan
26 tháng 3 2022 lúc 22:32
Câu d thôi ạ, câu a, b, c làm rồi ạ
23 tháng 10 2021 lúc 10:46
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
Đọc tiếp
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
Đúng 4
Bình luận (0)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
Đúng 1
Bình luận (0)
Mn giúp em câu b,c,d ạ, em cần gấp ạ
a) Thay \(x=\dfrac{1}{4}\) vào Q, ta được:
\(Q=\dfrac{1}{\dfrac{1}{4}\cdot\dfrac{1}{2}+27}=\dfrac{1}{27+\dfrac{1}{8}}=\dfrac{8}{217}\)
b) Ta có: \(P=\dfrac{x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}-\dfrac{1}{2-\sqrt{x}}-\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
\(=\dfrac{x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}+3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}-\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-9+\sqrt{x}+3-x+2\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3\sqrt{x}-6}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3}{\sqrt{x}+3}\)
c) Để \(P>\dfrac{1}{2}\) thì \(P-\dfrac{1}{2}>0\)
\(\Leftrightarrow\dfrac{6-\left(\sqrt{x}+3\right)}{2\left(\sqrt{x}+3\right)}>0\)
\(\Leftrightarrow3-\sqrt{x}>0\)
\(\Leftrightarrow x< 9\)
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0\le x< 9\\x\ne4\end{matrix}\right.\)
Đúng 3
Bình luận (0)
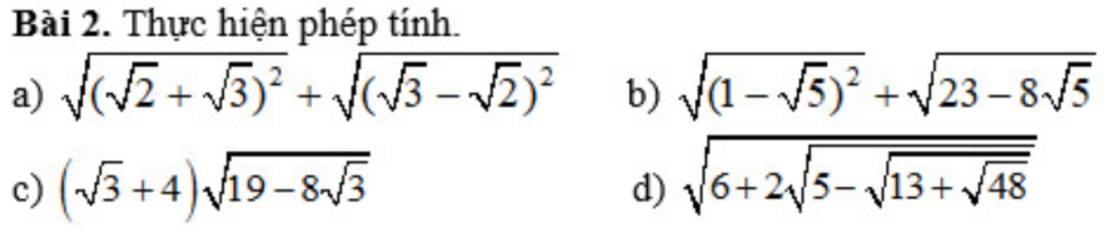câu b, c, d thôi ạ!
c: \(=\left(4+\sqrt{3}\right)\cdot\sqrt{\left(4-\sqrt{3}\right)^2}\)
=(4+căn 3)(4-căn 3)
=16-3=13
d: \(=\sqrt{6+2\sqrt{5-2\sqrt{3}-1}}\)
\(=\sqrt{6+2\cdot\sqrt{4-2\sqrt{3}}}\)
\(=\sqrt{6+2\cdot\left(\sqrt{3}-1\right)}=\sqrt{4+2\sqrt{3}}=\sqrt{3}+1\)
Đúng 2
Bình luận (0)
b) \(\sqrt{\left(1-\sqrt{5}\right)^2}+\sqrt{23-8\sqrt{5}}\)
\(=\left|1-\sqrt{5}\right|+\sqrt{23-2\sqrt{60}}\)
\(=\sqrt{5}-1+\sqrt{\left(\sqrt{20}\right)^2-2.\sqrt{20}.\sqrt{3}+\left(\sqrt{3}\right)^2}\)
\(=\sqrt{5}-1+\sqrt{\left(\sqrt{20}-\sqrt{3}\right)^2}\)
\(=\sqrt{5}-1+\sqrt{20}-\sqrt{3}=\sqrt{5}+2\sqrt{5}-1-\sqrt{3}\)
\(=3\sqrt{5}-1-\sqrt{3}\)
Đúng 0
Bình luận (0)
10 tháng 1 2021 lúc 20:36
Xem chi tiết
Gọi giao điểm AE và BP là F;
Gọi giao điểm QD và AB là H;
Gọi kéo dài AD cắt BF tại P'
Dễ cm M là trung điểm AC
Xét \(\Delta OMC\) có QD//CM\(\Rightarrow\dfrac{OD}{OM}=\dfrac{QD}{CM}\)(hệ quả tales)
Tương tự với \(\Delta OAM\) có \(\dfrac{OD}{OM}=\dfrac{DH}{AM}\)
\(\Rightarrow\dfrac{QD}{CM}=\dfrac{DH}{AM}\)
Mà CM=AM (vì M là tđ AC)
\(\Rightarrow QD=DH\)
Dễ cm P là trung điểm BF
Xét \(\Delta ABP'\) có DH//BP'
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{AD}{AP'}\)(tales)
Tương tự với \(\Delta AFP'\) có \(\dfrac{QD}{FP'}=\dfrac{AD}{AP'}\)
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{QD}{FP'}\)
Mà DH=QD (cmt)
\(\Rightarrow BP'=FP'\)
\(\Rightarrow\)P' là trung điểm BF
\(\Rightarrow P\equiv P'\)
\(\Rightarrow A,D,P\) thẳng hàng
Đúng 0
Bình luận (0)
mn ơi giúp mk câu b bài3 câu c,d bài4 ạ
thanks
\(\left(m-2\right)x^4-2\left(m+1\right)x^2+2m-1=0\left(1\right)\)
\(m=2\left(ktm\right)\)
\(m\ne2:đặt:x^2=t\ge0\Rightarrow\left(1\right)\Leftrightarrow\left(m-2\right)t^2-2\left(m+1\right)t+2m-1=0\)
\(3nghiem\Leftrightarrow\left\{{}\begin{matrix}2m-1=0\\t1+t2=\dfrac{2m+2}{m-2}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{1}{2}\\\left[{}\begin{matrix}m>2\\m< -1\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow m\in\phi\)
\(4nghiem\Leftrightarrow\left\{{}\begin{matrix}\Delta'>0\\t1+t2>0\Leftrightarrow\\t1.t2>0\end{matrix}\right.\left\{{}\begin{matrix}\left(m+1\right)^2-\left(m-2\right)\left(2m-1\right)>0\\\dfrac{2m+2}{m-2}>0\\\dfrac{2m-1}{m-2}>0\end{matrix}\right.\)
giải hệ bất pt trên=>m
\(c3:b;\left\{{}\begin{matrix}-8\le x\le-2\\m\left(x-3\right)\ge1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}-8\le x\le-2\\m\le\dfrac{1}{x-3}\end{matrix}\right.\)
\(có\) \(nghiệm\Leftrightarrow m\le max:\dfrac{1}{x-3}trên\left[-8;-2\right]\)
\(\Leftrightarrow m\le\dfrac{-1}{5}\)
Đúng 0
Bình luận (0)
làm câu a trc nhé ạ, lát em đăng câu b c d
a: \(A=\dfrac{3n^2+3n}{12n}=\dfrac{3n\left(n+1\right)}{3n\cdot4}=\dfrac{n+1}{4}\)
Vì 4=2^2 ko có thừa số nguyên tố nào khác 2 và 5
nên \(A=\dfrac{n+1}{4}\) viết được dưới dạng số thập phân hữu hạn
Đúng 2
Bình luận (0)
giúp mình câu b c d ạ
giúp em câu b d c ạ
b) Ta có: \(\left\{{}\begin{matrix}x-y\sqrt{2}=6\\2\sqrt{2}x-3y=8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x-3\sqrt{2}\cdot y=18\\4x-3\sqrt{2}\cdot y=8\sqrt{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-x=18-8\sqrt{2}\\x-y\sqrt{2}=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=8\sqrt{2}-18\\y\sqrt{2}=x-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=8\sqrt{2}-18\\y\sqrt{2}=8\sqrt{2}-18-6=8\sqrt{2}-24\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=8\sqrt{2}-18\\y=8-12\sqrt{2}\end{matrix}\right.\)
Vậy: hệ phương trình có nghiệm duy nhất là \(\left\{{}\begin{matrix}x=8\sqrt{2}-18\\y=8-12\sqrt{2}\end{matrix}\right.\)
c) Ta có: \(\left\{{}\begin{matrix}3x+2y=3\\5x+3y=10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}15x+10y=15\\15x+9y=30\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-15\\3x+2y=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x=3-2y=3-2\cdot\left(-15\right)=33\\y=-15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=11\\y=-15\end{matrix}\right.\)
Vậy: hệ phương trình có nghiệm duy nhất là \(\left\{{}\begin{matrix}x=11\\y=-15\end{matrix}\right.\)
d) Ta có: \(\left\{{}\begin{matrix}x-3y=23\\4x+5y=7\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x-12y=92\\4x+5y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-17y=85\\x-3y=23\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-5\\x=23+3y=23+3\cdot\left(-5\right)=8\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là (x,y)=(8;-5)
Đúng 1
Bình luận (0)
Giúp em với và cảm ơn ạ. Em cần giúp câu b, c, d ạ