Ai giúp m với ạ! Mình cảm ơn nhiều 😊 

Những câu hỏi liên quan
Ai giúp mình với cảm ơn nhiều 😊 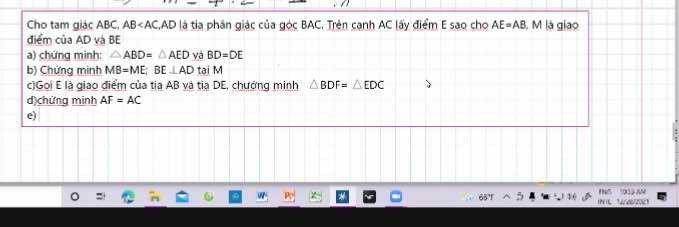
Mình đang cần gấp. Mọi người giúp mình với ạ! Mình cảm ơn nhiều! 😊
Chứng min rằng: 3n + 3/ 9n + 8 là phân số tối giản.
Ai HSG Toán thì giúp tớ với. Cảm ơn nhiều ạ!!! 😊😊😊
Để 3n + 3/ 9n + 8 là phân số tối giản thì nó phải có ƯCLN là 1
Đặt d là ƯCLN
=> (3n + 3)-(9n+8) chia hết cho d
=>3(3n+3)-(9n+8) chia hết cho d
=>9n+9-9n-8 chia hết cho d
=>1 chia hết cho d
=>ƯCLN(3n+3;9n+8)=1
=> (3n + 3)/(9n+8) tối giản
Đúng 0
Bình luận (0)
Gọi ƯCLN(3n + 3; 9n + 8) = d (d thuộc N*)
=> 3n + 3 chia hết cho d => 9n + 9 chia hết cho d
và 9n + 8 chia hết cho d
=> 9n + 9 - (9n + 8) chia hết cho d
=> 1 chia hết cho d, mà d thuộc N*
=> d = 1
=> ƯCLN(3n + 3; 9n + 8) = 1
=> \(\frac{3n+3}{9n+8}\)là phân số tối giản
Đúng 0
Bình luận (0)
Gọi d=ƯCLN(3n+3;9n+8) (d thuộc N*)
=> 3n+3 chia hết cho d và 9n+8 chia hết cho d
Do 3n+3 chia hết cho d =>3(3n+3) chia hết cho d . Hay 9n+9 chia hết cho d
Mà 9n+8 chia hết cho d
Nên : (9n+9)-(9n+8) chia hết cho d
=> 1 chia hết cho d
=> d thuộc tập hợp ước của 1. Mà d thuộc N*
=>d=1
Hay ƯCLN (3n+3;9n+8)=1
=> 3n+3/9n+8 là phân số tối giản
tk cho mik nha
Đúng 0
Bình luận (0)
Trời ơi ! Ai cứu mình với , giúp mình 2 cái bài này đc ko ? Mình đang cần gấp ạ ! Cảm ơn trc nhen 😊
Trời trời giúp mình với mấy thần đồng tiếng anh ơi , mình sắp toang ròi 😢😢😢
Đúng 0
Bình luận (1)
Ai giúp mình với ạ mình cảm ơn nhiều ạ .
CÂU 1:
\(\dfrac{6x^2y^2}{8xy^5}=\dfrac{3x}{4y^3}\)
CÂU 2:
\(\dfrac{12x^3y^2}{18xy^5}=\dfrac{2x^2}{3y^3}\)
CÂU 3:
\(\dfrac{15x\left(x+5\right)^3}{20x^2\left(x+5\right)}=\dfrac{3\left(x+5\right)^2}{4x}\)
CÂU 4:
\(\dfrac{3xy+x}{9y+3}=\dfrac{x\left(3y+1\right)}{3\left(3y+1\right)}=\dfrac{x}{3}\)
CÂU 5:
\(\dfrac{3xy+3x}{9y+9}=\dfrac{3x\left(y+1\right)}{9\left(y+1\right)}=\dfrac{x}{3}\)
CÂU 6:
\(\dfrac{x^2-xy}{5y^2-5xy}=\dfrac{x\left(x-y\right)}{5y\left(y-x\right)}=\dfrac{-x\left(y-x\right)}{5y\left(y-x\right)}=\dfrac{-x}{5y}\)
CÂU 7:
\(\dfrac{2x^2+2x}{x+1}=\dfrac{2x\left(x+1\right)}{x+1}=2x\)
CÂU 8:
\(\dfrac{7x^2+14x+7}{3x^2+3x}=\dfrac{7\left(x^2+2x+1\right)}{3x\left(x+1\right)}\\ =\dfrac{7\left(x+1\right)^2}{3x\left(x+1\right)}=\dfrac{7\left(x+1\right)}{3x}\)
CÂU 9:
\(\dfrac{10xy^2\left(x+y\right)}{15xy\left(x+y\right)^3}=\dfrac{2y}{3\left(x+y\right)^2}\)
Đúng 0
Bình luận (0)
Giúp e câu c với ạ e cảm ơn ạ😊😊😊😊
\(a,2KMnO_4\rightarrow\left(t^o\right)K_2MnO_2+MnO_2+O_2\\ b,n_{KMnO_4}=\dfrac{31,6}{158}=0,2\left(mol\right)\\ \Rightarrow n_{O_2}=\dfrac{0,2}{2}=0,1\left(mol\right)\\ \Rightarrow V_{O_2\left(đktc\right)}=0,1.22,4=2,24\left(l\right)\\ c,n_{Fe}=\dfrac{11,2}{56}=0,2\left(mol\right)\\ 3Fe+2O_2\rightarrow\left(t^o\right)Fe_3O_4\\ Vì:\dfrac{0,2}{3}< \dfrac{0,1}{2}\Rightarrow Fedư\\ \Rightarrow n_{Fe_3O_4}=n_{O_2}:2=0,1 :2=0,05\left(mol\right)\\ \Rightarrow m_{Fe_3O_4}=232.0,05=11,6\left(g\right)\)
Đúng 4
Bình luận (0)
 ai giúp mình với ạ, mình cảm ơn rất nhiều
ai giúp mình với ạ, mình cảm ơn rất nhiều
Gọi điện trở ampe kế là Ra
Hiệu điện thế hai đầu ampe kế A2 là:
\(UA2=I2.Ra=1.Ra=Ra\)
Mà ta lại có: \(UA2=UA3+IA3.2r=IA3.Ra+IA3.2r=0.5Ra+0.5.2r=0.5Ra+r\)
=> \(Ra=0.5Ra+r\)
=> \(r=0.5Ra\)
Ta có: \(IMP=IA2+IA3=1+0.5=1.5\left(A\right)\)
=>\(UMP=IMP.r=1.5r=1,5.0.5Ra=0.75Ra\)
=>\(UMQ=UMP+UA2=0.75Ra+Ra=1.75Ra\)
=> Cường độ dong điện chạy qua ampe kế A1 là:
\(IA1=\dfrac{UMQ}{Ra}=\dfrac{1.75Ra}{Ra}=1.75\left(A\right)\)
Đúng 0
Bình luận (0)
ai giúp mình bài này với ạ, mình cảm ơn nhiều ![]()

c)\(\left\{{}\begin{matrix}u_1+u_3=3\\u_1^2+u_3^2=5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}u_1+u_3=3\\\left(u_1+u_3\right)^2-2u_1u_3=5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}u_1+u_3=3\\u_1u_3=2\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}u_1=2\\u_3=1\end{matrix}\right.\\\left\{{}\begin{matrix}u_1=1\\u_3=2\end{matrix}\right.\end{matrix}\right.\)
Làm nốt (sử dụng công thức: \(u_n=u_1+\left(n-1\right)d\) để tìm được công sai
\(S_n=nu_1+\dfrac{n\left(n-1\right)}{2}d\) để tính tổng 15 số hạng đầu)
d)\(\left\{{}\begin{matrix}u_1+u_2+u_3=14\\u_1u_2u_3=64\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}u_2-d+u_2+u_2+d=14\\\left(u_2-d\right)u_2\left(u_2+d\right)=64\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_2=\dfrac{14}{3}\\\left(u_2^2-d^2\right)u_2=64\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\dfrac{14}{3}=u_2=u_1+d\\d=\dfrac{2\sqrt{889}}{21}\end{matrix}\right.\\\left\{{}\begin{matrix}\dfrac{14}{3}=u_1+d\\d=\dfrac{-2\sqrt{889}}{21}\end{matrix}\right.\end{matrix}\right.\)
(Làm nốt,số xấu quá)
e)\(\left\{{}\begin{matrix}u_1+u_2+u_3=7\\u_1^2+u_2^2+u_3^2=21\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1+u_2+u_3=7\\u_1u_2u_3=\dfrac{21-\left(u_1+u_2+u_3\right)^2}{2}=-14\end{matrix}\right.\)
Làm như ý d)
Đúng 1
Bình luận (1)
Ai giúp mình phiếu này với ạ mình cảm ơn nhiều

Ai giúp mình giải tự luận bài này với ạ!! Mình cảm ơn nhiều ạ!
`sin3x sinx+sin(x-π/3) cos (x-π/6)=0`
`<=> 1/2 (cos2x - cos4x) + 1/2(-sin π/6 + sin (2x-π/2)=0`
`<=> cos2x-cos4x-1/2+ sin(2x-π/2)=0`
`<=>cos2x-cos4x-1/2+ sin2x .cos π/2 - cos2x. sinπ/2=0`
`<=> cos2x - cos4x - cos2x = 1/2`
`<=> cos4x = cos(2π)/3`
`<=>` \(\left[{}\begin{matrix}4x=\dfrac{2\text{π}}{3}+k2\text{π}\\4x=\dfrac{-2\text{π}}{3}+k2\text{π}\end{matrix}\right.\)
`<=>` \(\left[{}\begin{matrix}x=\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\\x=-\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\end{matrix}\right.\)
Đúng 1
Bình luận (1)
\(sin3x.sinx+sin\left(x-\dfrac{\pi}{3}\right)cos\left(x-\dfrac{\pi}{6}\right)=0\)
\(\Leftrightarrow\dfrac{1}{2}cos2x-\dfrac{1}{2}cos4x+\dfrac{1}{2}sin\left(2x-\dfrac{\pi}{2}\right)+\dfrac{1}{2}sin\left(-\dfrac{\pi}{6}\right)=0\)
\(\Leftrightarrow\dfrac{1}{2}cos2x-\dfrac{1}{2}cos4x-\dfrac{1}{2}cos2x-\dfrac{1}{4}=0\)
\(\Leftrightarrow cos4x+\dfrac{1}{2}=0\)
\(\Leftrightarrow2cos^22x-1+\dfrac{1}{2}=0\)
\(\Leftrightarrow cos^22x=\dfrac{1}{4}\)
\(\Rightarrow cos2x=\pm\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời






















