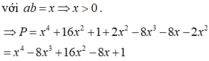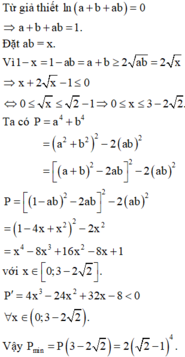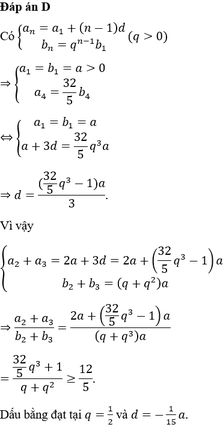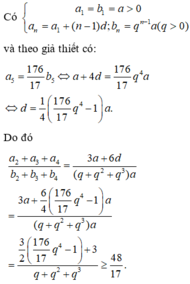Cho a+b=1. Tìm giá trị nhỏ nhất của a4+ b4

Những câu hỏi liên quan
Cho a, b 0 thỏa mãn điều kiện a + b + ab 1, giá trị nhỏ nhất của
P
a
4
+
b
4
l
à
x
(
x
-
y
)
4
(
x
,
y
∈
N
)
. Giá trị của x + y là A. 3 B. 5 C. 7 D. 9
Đọc tiếp
Cho a, b > 0 thỏa mãn điều kiện a + b + ab = 1, giá trị nhỏ nhất của P = a 4 + b 4 l à x ( x - y ) 4 ( x , y ∈ N ) . Giá trị của x + y là
A. 3
B. 5
C. 7
D. 9
Với a,b 0 thỏa mãn điều kiện a + b +ab 1, giá trị nhỏ nhất của
P
a
4
+
b
4
bằng. A. B. C. D.
Đọc tiếp
Với a,b > 0 thỏa mãn điều kiện a + b +ab = 1, giá trị nhỏ nhất của P = a 4 + b 4 bằng.
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho các số thực a và b thỏa mãn:
(
2
+
a
)
(
1
+
b
)
9
2
Giá trị nhỏ nhất của biểu thức:
P
16
+
a
4
+
4
1
+
b
4
nằm trong khoảng A. (8,1;8,3) B. (4;4,2) C. (8,3...
Đọc tiếp
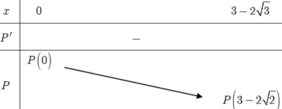
Cho các số thực a và b thỏa mãn: ( 2 + a ) ( 1 + b ) = 9 2 Giá trị nhỏ nhất của biểu thức: P = 16 + a 4 + 4 1 + b 4 nằm trong khoảng
A. (8,1;8,3)
B. (4;4,2)
C. (8,3;8,5)
D. (12,4;12,6)
Với a,b 0 thỏa mãn điều kiện ln(a + b +ab) giá trị nhỏ nhất của
P
a
4
+
b
4
bằng A.
2
+
1
4
.
B.
2
2...
Đọc tiếp
Với a,b > 0 thỏa mãn điều kiện ln(a + b +ab) giá trị nhỏ nhất của P = a 4 + b 4 bằng
A. 2 + 1 4 .
B. 2 2 − 1 4 .
C. 2 − 1 4 .
D. 2 2 + 1 4 .
giúp em với em đang cần gấp ạ
Cho biểu thức P =a4+b4-ab,với a,b là các số thực thoả mãn
a2+b2+ab=3.Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P
https://tuhoc365.vn/qa/cho-bieu-thuc-p-a4-b4-ab-voi-ab-la-cac-so-thuc-thoa-man-a2-b2-ab-3-tim-gia-tri-lon/
Bạn có thể tham khảo ở đây nha.
Đúng 0
Bình luận (0)
Với các số dương a, b thỏa mãn: (2a-1)2 + (2b-1)2 = 2
Tìm giá trị nhỏ nhất của biểu thức P = a4 + b4 + 2020/(a+b)2
Mong mọi người giúp mình câu này ạ, càng chi tiết càng tốt. Mình xin cảm ơn
Cho các số thực dương
a
1
,
a
2
,
a
3
,
a
4
theo thứ tự lập thành một cấp số cộng và các số thực dương
b
1
,
b
2
,
b
3
,
b
4
theo thứ tự lập thành cấp số nhân...
Đọc tiếp
Cho các số thực dương a 1 , a 2 , a 3 , a 4 theo thứ tự lập thành một cấp số cộng và các số thực dương b 1 , b 2 , b 3 , b 4 theo thứ tự lập thành cấp số nhân. Biết rằng a 1 = b 1 và a 4 = 32 5 b 4 . Giá trị nhỏ nhất của biểu thức a 2 + a 3 b 2 + b 3 bằng
A. 16 5
B. 11 5
C. 17 5
D. 12 5
Tính giá trị của biểu thức a4 + b4 + c4, biết rằng a + b + c =1,ab+bc+ca=-1 và abc=-1
Lời giải:
$a^4+b^4+c^4=(a^2+b^2+c^2)^2-2(a^2b^2+b^2c^2+c^2a^2)$
$=[(a+b+c)^2-2(ab+bc+ac)]^2-2[(ab+bc+ac)^2-2abc(a+b+c)]$
$=[1^2-2(-1)]^2-2[(-1)^2-2(-1).1]=3$
Đúng 0
Bình luận (0)
Cho a+b = -3, ab = -2. Hãy tính giá trị của:
a2 + b2, a4 + b4, a3 + b3, a5 + b5, a7 + b7.
\(a^2+b^2=\left(a+b\right)^2-2ab=\left(-3\right)^2-2\cdot\left(-2\right)=9+4=13\)
\(a^3+b^3=\left(a+b\right)^3-3ab\left(a+b\right)\)
\(=\left(-3\right)^3-3\cdot\left(-2\right)\cdot\left(-3\right)\)
\(=-27-18=-45\)
Đúng 0
Bình luận (0)
Cho các số thực dương
a
1
,
a
2
,
a
3
,
a
4
,
a
5
theo thứ tự lập thành cấp số cộng và các số thực dương
b
1
,
b
2
,
b
3
,...
Đọc tiếp
Cho các số thực dương a 1 , a 2 , a 3 , a 4 , a 5 theo thứ tự lập thành cấp số cộng và các số thực dương b 1 , b 2 , b 3 , b 4 , b 5 theo thứ tự lập thành cấp số nhân. Biết rằng a 1 = b 1 và a 5 = 176 17 b 5 Giá trị nhỏ nhất của biểu thức a 2 + a 3 + a 4 b 2 + b 3 + b 4 bằng
A. 16 17
B. 48 17
C. 32 17
D. 24 17