Giúp mik với ạ mk đăng cần gấp giải bằng pt

Những câu hỏi liên quan
giải pt: \(\dfrac{x+1}{3}=x+3\)
giúp mk vs ạ mk cần gấp
\(\Leftrightarrow x+1=3x+9\\ \Leftrightarrow2x=-8\\ \Leftrightarrow x=-4\)
Đúng 1
Bình luận (0)
1) giải pt:
\(\sqrt{x-3}-2\sqrt{x^2-9}=0\)
giúp mk vs ạ mk cần gấp
ĐKXĐ: \(x\ge3\)
\(\Leftrightarrow\sqrt{x-3}=2\sqrt{x^2-9}\)
\(\Leftrightarrow x-3=4\left(x-3\right)\left(x+3\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\4\left(x+3\right)=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{11}{4}\left(loại\right)\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Giải giúp mình pt này với, cần gấp ạ 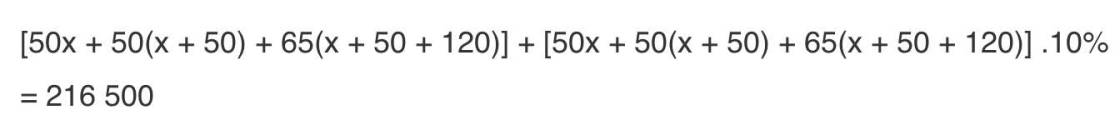
=>(50x+50x+250+65x+11050)*1,1=216500
=>165x+11300=196818,1818
=>165x=185518,1818
=>\(x\simeq124.353\)
Đúng 0
Bình luận (0)
 giúp mik với ạ mik cần gấp. GIẢI CỤ THỂ GIÚP MIK vs ạ
giúp mik với ạ mik cần gấp. GIẢI CỤ THỂ GIÚP MIK vs ạ
`@` `\text {Ans}`
`\downarrow`
`4,`
Vì `\text {MN // BC}`
`=>` $\widehat {B} = \widehat {BMN} = 114^0 (\text {2 góc đối đỉnh})$
Ta có: \(\left\{{}\begin{matrix}\widehat{\text{BMN}}+\widehat{\text{AMN}}=180^0\left(\text{2 góc kề bù}\right)\\\widehat{\text{CNM}}+\widehat{\text{ANM}}=180^0\left(\text{2 góc kề bù}\right)\end{matrix}\right.\)
`=>`\(\left\{{}\begin{matrix}\widehat{\text{AMN}}=180^0-114^0=66^0\\\widehat{\text{ANM}}=180^0-130^0=50^0\end{matrix}\right.\)
Xét `\Delta AMN`:
\(\widehat{\text{A}}+\widehat{\text{M}}+\widehat{\text{N}}=180^0\left(\text{định lý tổng 3 góc trong 1 tgiac}\right)\)
`=>`\(\widehat{\text{A}}+66^0+50^0=180^0\)
`=>`\(\widehat{\text{A}}=180^0-66^0-50^0=64^0\)
Mà \(\widehat{\text{A}}=\widehat{\text{x}}\)
`=>`\(\widehat{\text{x}}=64^0\)
Vậy, số đo của góc `x = 64^0.`
Đúng 3
Bình luận (2)
Giải giúp mik câu đại với ạ , giúp mik vẽ hình bài hình luoon đc ko ạ !! Giúp mik với mik cần gấp lắm !! Các bạn giải chi tiết giúp mik
Câu 3:
a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)
b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)
nên BC<AC=AB
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
Đúng 2
Bình luận (0)
Câu 2
a) Thay y = -2 vào biểu thức đã cho ta được:
2.(-2) + 3 = -1
Vậy giá trị của biểu thức đã cho tại y = -2 là -1
b) Thay x = -5 vào biểu thức đã cho ta được:
2.[(-5)² - 5] = 2.(25 - 5) = 2.20 = 40
Vậy giá trị của biểu thức đã cho tại x = -5 là 40
Đúng 0
Bình luận (0)
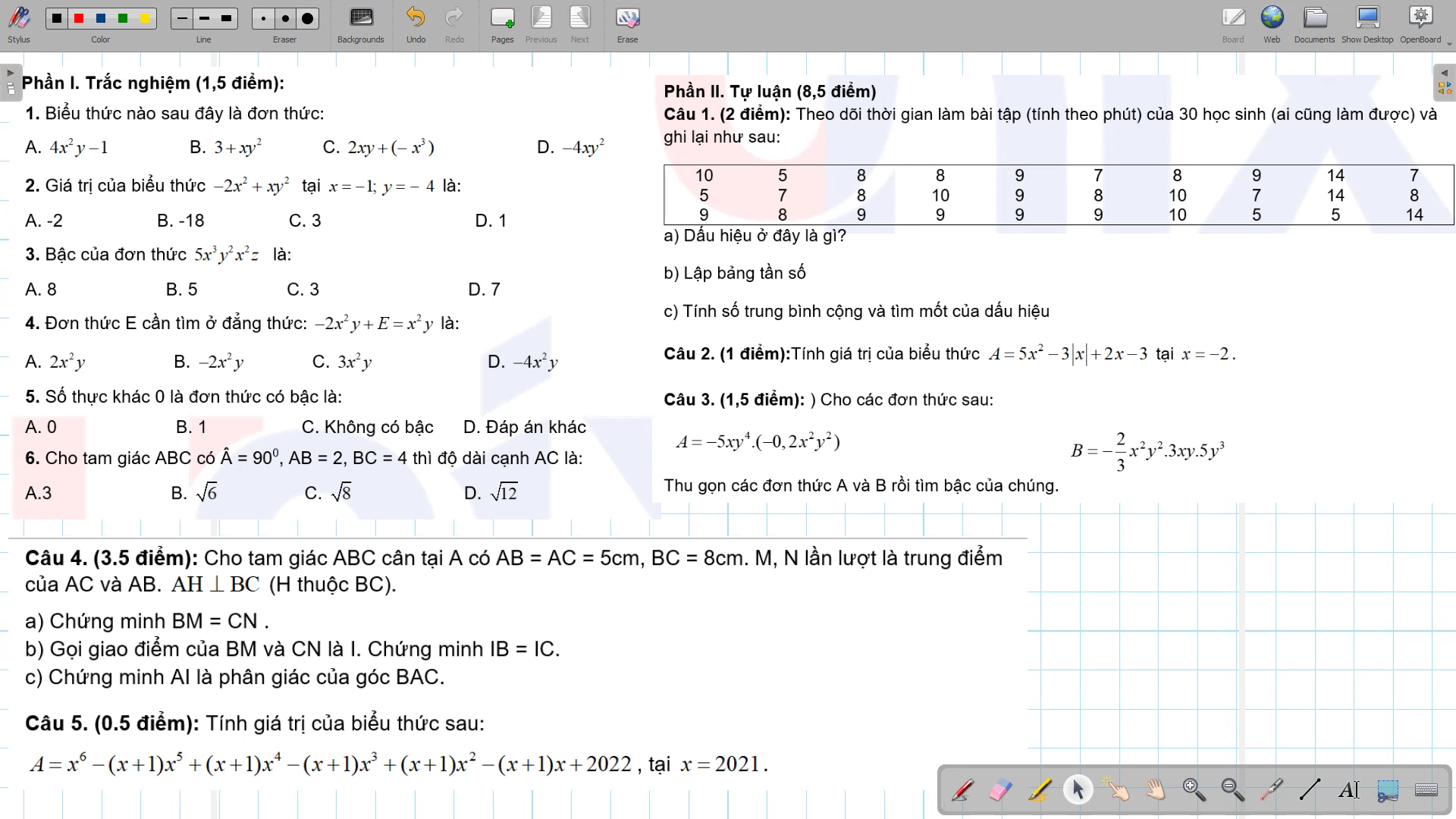
giải giúp mik câu 4 hình học đc k ạ, mk đag cần gấp
4:
a: Xét ΔABM và ΔACN có
AB=AC
góc A chung
AM=AN
=>ΔABM=ΔACN
=>BM=CN
b: Xét ΔNBC và ΔMCB có
NB=MC
góc NBC=góc MCB
BC chung
=>ΔNBC=ΔMCB
=>góc IBC=góc ICB
=>IB=IC
c: Xét ΔABI và ΔACI có
AB=AC
IB=IC
AI chung
=>ΔABI=ΔACI
=>góc BAI=góc CAI
=>AI là phân giác của góc BAC
Đúng 0
Bình luận (0)
Giải giúp mik với ạ, mik đg cần gấp
Giải giúp mik với ạ mik đang cần gấp
(2) giải các pt sau bằng công thức nghiệm (hoặc công thức nghiện thu gọn)
1) \(x^2-11x+30=0\)
2) \(x^2-x-20=0\)
3) \(x^2+14x+24=0\)
4) \(3x^2+8x-2=0\)
giúp mk vs ạ mk đang cần gấp
\(1,\Delta=\left(-11\right)^2-4\cdot30=1\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{11-1}{2}=5\\x=\dfrac{11+1}{2}=6\end{matrix}\right.\\ 2,\Delta=\left(-1\right)^2-4\left(-20\right)=81\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1-\sqrt{81}}{2}=-4\\x=\dfrac{1+\sqrt{81}}{2}=5\end{matrix}\right.\\ 3,\Delta=14^2-4\cdot24=100\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-14-\sqrt{100}}{2}=-12\\x=\dfrac{-14+\sqrt{100}}{2}=-2\end{matrix}\right.\\ 4,\Delta=8^2-4\left(-2\right)3=88\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-8-\sqrt{88}}{6}=\dfrac{-4+\sqrt{22}}{3}\\x=\dfrac{-8+\sqrt{88}}{6}=\dfrac{-4-\sqrt{22}}{3}\end{matrix}\right.\)
Đúng 2
Bình luận (1)
1) Δ = (-11)2 -4.1.30 = 1 > 0 ⇒ Phương trình đã cho có hai nghiệm phân biệt, \(\sqrt{\Delta}\)=1.
x1 = \(\dfrac{-\left(-11\right)+1}{2.1}\) = 6, x2 = \(\dfrac{-\left(-11\right)-1}{2.1}\) = 5.
2) Δ = (-1)2 -4.1.(-20) = 81 > 0 ⇒ Phương trình đã cho có hai nghiệm phân biệt, \(\sqrt{\Delta}\)=9.
x1 = \(\dfrac{-\left(-1\right)+9}{2.1}\) = 5, x2 = \(\dfrac{-\left(-1\right)-9}{2.1}\) = -4.
3) Δ' = 72 -1.24 = 25 > 0 ⇒ Phương trình đã cho có hai nghiệm phân biệt, \(\sqrt{\Delta'}\)=5.
x1 = \(\dfrac{-7+5}{1}\) = -2, x2 = \(\dfrac{-7-5}{1}\) = -12.
4) Δ' = 42 -3.(-2) = 22 > 0 ⇒ Phương trình đã cho có hai nghiệm phân biệt, \(\sqrt{\Delta'}\)=\(\sqrt{22}\).
x1 = \(\dfrac{-4+\sqrt{22}}{3}\), x2 = \(\dfrac{-4-\sqrt{22}}{3}\).
Đúng 0
Bình luận (0)
Giải chi tiết pt 3 và 4 giúp em với ạ. Em đang cần gấp. Em cảm ơn ạ
4.
\(sinx+2cos\left(x+\dfrac{\pi}{3}\right)+4sin\left(x+\dfrac{\pi}{6}\right)+cosx=4\)
\(\Leftrightarrow sinx+cosx-\sqrt{3}sinx+2\sqrt{3}sinx+2cosx+cosx=4\)
\(\Leftrightarrow\left(1+\sqrt{3}\right)sinx+4cosx=4\)
\(\Leftrightarrow\sqrt{20+2\sqrt{3}}\left(\dfrac{1+\sqrt{3}}{\sqrt{20+2\sqrt{3}}}sinx+\dfrac{4}{\sqrt{20+2\sqrt{3}}}cosx\right)=4\)
\(\Leftrightarrow cos\left(x-arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}\right)=\dfrac{4}{\sqrt{20+2\sqrt{3}}}\)
\(\Leftrightarrow x-arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}=\pm arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}+k2\pi\\x=k2\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
3.
\(4sinx+cosx+2cos\left(x+\dfrac{\pi}{3}\right)=2\)
\(\Leftrightarrow4sinx+cosx+cosx-\sqrt{3}sinx=2\)
\(\Leftrightarrow\left(4-\sqrt{3}\right)sinx+2cosx=2\)
\(\Leftrightarrow\sqrt{23-4\sqrt{3}}\left(\dfrac{4-\sqrt{3}}{\sqrt{23-4\sqrt{3}}}sinx+\dfrac{2}{\sqrt{23-4\sqrt{3}}}cosx\right)=2\)
\(\Leftrightarrow cos\left(x-arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}\right)=\dfrac{2}{\sqrt{23-4\sqrt{3}}}\)
\(\Leftrightarrow x-arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}=\pm arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}+k2\pi\\x=k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)

























