2x3+5x2-22x+15 : 2x-3

Những câu hỏi liên quan
a, ( 2x3 + 5x2 - 2x + 3 ) : ( 2x2 - x + 1 )
b, ( 2x3 - 5x2 + 6x -15 ) : ( 2x - 5 )
\(a,=\left(2x^3-x^2+x+4x^2-2x+2-x+1\right):\left(2x^2-x+1\right)\\ =\left[x\left(2x^2-x+1\right)+2\left(2x^2-x+1\right)-x+1\right]:\left(2x^2-x+1\right)\\ =x+2\left(\text{dư }-x+1\right)\\ b,=\left[x^2\left(2x-5\right)+3\left(2x-5\right)\right]:\left(2x-5\right)\\ =x^2+3\)
Đúng 3
Bình luận (0)
1. (x3 – 3x2 + x – 3) : (x – 3) 2. (2x4 – 5x2 + x3 – 3 – 3x) : (x2 – 3) 3. (x – y – z)5 : (x – y – z)3 4. (x2 + 2x + x2 – 4) : (x + 2) 5. (2x3 + 5x2 – 2x + 3) : (2x2 – x + 1) 6. (2x3 – 5x2 + 6x – 15) : (2x – 5)
1: \(=x^2+1\)
3: \(=\left(x-y-z\right)^2\)
Đúng 1
Bình luận (0)
Giải các phương trình:
a
)
5
x
2
−
3
x
+
1
2
x
+
11
b
)
x
2
5...
Đọc tiếp
Giải các phương trình:
a ) 5 x 2 − 3 x + 1 = 2 x + 11 b ) x 2 5 − 2 x 3 = x + 5 6 c ) x x − 2 = 10 − 2 x x 2 − 2 x d ) x + 0 , 5 3 x + 1 = 7 x + 2 9 x 2 − 1 e ) 2 3 x 2 + x + 1 = 3 ( x + 1 ) f ) x 2 + 2 2 x + 4 = 3 ( x + 2 )
a)
5 x 2 − 3 x + 1 = 2 x + 11 ⇔ 5 x 2 − 3 x + 1 − 2 x − 11 = 0 ⇔ 5 x 2 − 5 x − 10 = 0
Có a = 5; b = -5; c = -10 ⇒ a - b + c = 0
⇒ Phương trình có hai nghiệm: x 1 = - 1 v à x 2 = - c / a = 2 .
Vậy phương trình có tập nghiệm S = {-1; 2}.
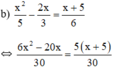
⇔ 6 x 2 − 20 x = 5 ( x + 5 ) ⇔ 6 x 2 − 20 x − 5 x − 25 = 0 ⇔ 6 x 2 − 25 x − 25 = 0
Có a = 6; b = -25; c = -25
⇒ Δ = ( - 25 ) 2 – 4 . 6 . ( - 25 ) = 1225 > 0
⇒ Phương trình có hai nghiệm
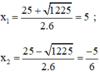
Vậy phương trình có tập nghiệm 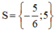
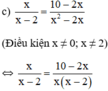
⇔ x 2 = 10 − 2 x ⇔ x 2 + 2 x − 10 = 0
Có a = 1; b = 2; c = -10 ⇒ Δ ’ = 1 2 – 1 . ( - 10 ) = 11 > 0
⇒ Phương trình có hai nghiệm
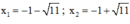
Cả hai nghiệm đều thỏa mãn điều kiện xác định.
Vậy phương trình có tập nghiệm 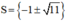
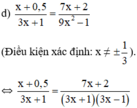
⇔ ( x + 0 , 5 ) ⋅ ( 3 x − 1 ) = 7 x + 2 ⇔ 3 x 2 + 1 , 5 x − x − 0 , 5 = 7 x + 2 ⇔ 3 x 2 − 6 , 5 x − 2 , 5 = 0
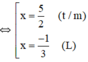
Vậy phương trình có tập nghiệm 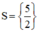
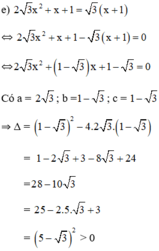
⇒ Phương trình có hai nghiệm
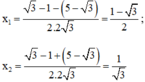
Vậy phương trình có tập nghiệm 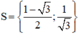
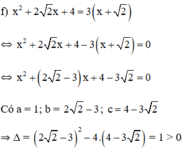
Phương trình có hai nghiệm:
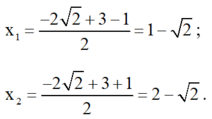
Vậy phương trình có tập nghiệm ![]()
Đúng 0
Bình luận (0)
Cứu với ạ
Làm tính chia
1) (x3 – 3x2 + x – 3) : (x – 3) 2) (2x4 – 5x2 + x3 – 3 – 3x) : (x2 – 3)
3) (x – y – z)5 : (x – y – z)3 4) (x2 + 2x + x2 – 4) : (x + 2)
| 5) (2x3 + 5x2 – 2x + 3) : (2x2 – x + 1) | 6) (2x3 – 5x2 + 6x – 15):(2x – 5) |
(2x3-5x2+6x-15):(2x-5)
\(\left(2x^3+5x^2+6x-15\right):\left(2x-5\right)=\left[x^2\left(2x-5\right)+3\left(2x-5\right)\right]:\left(2x-5\right)=\left[\left(2x-5\right)\left(x^2+3\right)\right]:\left(2x-5\right)=x^2+3\)
Đúng 1
Bình luận (0)
Thực hiện phép chia:
1. (-3x3 + 5x2 - 9x + 15) : ( 3x + 5)
2. ( 5x4 + 9x3 - 2x2 - 4x - 8) : ( x-1)
3. ( 5x3 + 14x2 + 12x + 8 ) : (x + 2)
4. ( x4 - 2x3 + 2x -1 ) : ( x2 - 1)
5. ( 5x2 - 3x3 + 15 - 9x ) : ( 5 - 3x)
6. ( -x2 + 6x3 - 26x + 21) : ( 3 -2x )
1: Sửa đề: 3x-5
\(=\dfrac{-x^2\left(3x-5\right)-3\left(3x-5\right)}{3x-5}=-x^2-3\)
2: \(=\dfrac{5x^4-5x^3+14x^3-14x^2+12x^2-12x+8x-8}{x-1}\)
=5x^2+14x^2+12x+8
3: \(=\dfrac{5x^3+10x^2+4x^2+8x+4x+8}{x+2}=5x^2+4x+4\)
4: \(=\dfrac{\left(x^2-1\right)\left(x^2+1\right)-2x\left(x^2-1\right)}{x^2-1}=x^2+1-2x\)
5: \(=\dfrac{x^2\left(5-3x\right)+3\left(5-3x\right)}{5-3x}=x^2+3\)
Đúng 3
Bình luận (0)
Giải PT
1 ) (2x + 1)(3x – 2) = (5x – 8)(2x + 1)
2) 4x2 -1 = (2x + 1)(3x – 5)
3) (x + 1)2 = 4(x2 – 2x + 1)
4) 2x3+ 5x2 – 3x = 0
5) {2x{ = 3x – 2
6) x + 15 = 3x – 1
7) 2 – x = 0,5x – 4
1) (2x + 1)(3x – 2) = (5x – 8)(2x + 1)
⇔ (2x + 1)(3x – 2) – (5x – 8)(2x + 1) = 0
⇔ (2x + 1).[(3x – 2) – (5x – 8)] = 0
⇔ (2x + 1).(3x – 2 – 5x + 8) = 0
⇔ (2x + 1)(6 – 2x) = 0
⇔\(\left[{}\begin{matrix}2x+1=0\\6-2x=0\end{matrix}\right.\) ⇔ \(\left[{}\begin{matrix}x=\dfrac{-1}{2}\\x=3\end{matrix}\right.\)
Vậy.....
2) 4x2 -1 = (2x + 1)(3x - 5)
⇔ (2x-1)(2x+1)-(2x+1)(3x-5)=0
⇔ (2x+1)(2x-1-3x+5)=0
⇔ (2x+1)(4-x)=0
⇔ \(\left[{}\begin{matrix}2x+1=0\\4-x=0\end{matrix}\right.\) ⇔ \(\left[{}\begin{matrix}x=\dfrac{-1}{2}\\x=4\end{matrix}\right.\)
Vậy...
3)
(x + 1)2 = 4(x2 – 2x + 1)
⇔ (x + 1)2 - 4(x2 – 2x + 1) = 0
⇔ x2 + 2x +1- 4x2 + 8x – 4 = 0
⇔ - 3x2 + 10x – 3 = 0
⇔ (- 3x2 + 9x) + (x – 3) = 0
⇔ -3x (x – 3)+ ( x- 3) = 0
⇔ ( x- 3) ( - 3x + 1) = 0
⇔\(\left[{}\begin{matrix}x-3=0\\-3x+1=0\end{matrix}\right.\) ⇔\(\left[{}\begin{matrix}x=3\\x=\dfrac{1}{3}\end{matrix}\right.\)
Vậy......
Đúng 2
Bình luận (0)
4) 2x3+5x2-3x=0
⇒2x3-x2+6x2-3x=0
⇒(2x3-x2)+(6x2-3x)=0
⇒x2(2x-1)+3x(2x-1)=0
⇒(x2+3x)(2x-1)=0
⇒ hoặc x2+3x=0⇒x(x+3)=0⇒hoặc x=0 hoặc x=-3
hoặc 2x-1=0⇒x=0,5
Vậy ...
5)2x=3x-2
⇒2x-3x=-2
⇒-x=-2
⇒x=2
6) x+15=3x-1
⇒x-3x=-1-15
⇒-2x=-16
⇒x=8
7)2-x=0,5x-4
⇒-x-0,5x=-4-2
⇒-1,5x=-6
⇒x=4
Đúng 0
Bình luận (0)
thực hiện phép chia
(-3x3 + 5x2 - 9x + 15) : (-3 + 5)
(x4 - 2x3 + 2x -1) : (x2 - 1)
(5x4 + 9x3 - 2x2 - 4x -8) : (x-1)
(5x3 + 14x2 + 12x + 8) : (x+2)
c) Ta có: \(\dfrac{5x^4+9x^3-2x^2-4x-8}{x-1}\)
\(=\dfrac{5x^4-5x^3+14x^3-14x^2+12x^2-12x+8x-8}{x-1}\)
\(=\dfrac{5x^3\left(x-1\right)+14x^2\left(x-1\right)+12x\left(x-1\right)+8\left(x-1\right)}{x-1}\)
\(=5x^3+14x^2+12x+8\)
d) Ta có: \(\dfrac{5x^3+14x^2+12x+8}{x+2}\)
\(=\dfrac{5x^3+10x^2+4x^2+8x+4x+8}{x+2}\)
\(=\dfrac{5x^2\left(x+2\right)+4x\left(x+2\right)+4\left(x+2\right)}{x+2}\)
\(=5x^2+4x+4\)
Đúng 1
Bình luận (0)
thực hiện phép chia
(-3x3 + 5x2 - 9x + 15) : (-3 + 5)
(x4 - 2x3 + 2x -1) : (x2 - 1)
(5x4 + 9x3 - 2x2 - 4x -8) : (x-1)
(5x3 + 14x2 + 12x + 8) : (x+2)
c) Ta có: \(\dfrac{5x^4+9x^3-2x^2-4x-8}{x-1}\)
\(=\dfrac{5x^4-5x^3+14x^3-14x^2+12x^2-12x+8x-8}{x-1}\)
\(=\dfrac{5x^3\left(x-1\right)+14x^2\left(x-1\right)+12x\left(x-1\right)+8\left(x-1\right)}{x-1}\)
\(=5x^3+14x^2+12x+8\)
Đúng 0
Bình luận (0)
1) (1-x)(5x+3)=(3x-7)(x-1)
2) (x-2)(x+1)=x2-4
3) 2x3+3x2-32x=48
4) x2+2x-15=0
5) 2x(2x-3)=(3-2x)(2-5x)
6) x3-5x2+6x=0
7) (x2-5)(x+3)=0
8) (x+7)(3x-1)=49-x2
\(\left(1-x\right)\left(5x+3\right)=\left(3x-7\right)\left(x-1\right)\)
\(< =>\left(1-x\right)\left(5x+3+3x-7\right)=0\)
\(< =>\left(1-x\right)\left(8x-4\right)=0\)
\(< =>\orbr{\begin{cases}1-x=0\\8x-4=0\end{cases}< =>\orbr{\begin{cases}x=1\\x=\frac{1}{2}\end{cases}}}\)
\(\left(x-2\right)\left(x+1\right)=x^2-4\)
\(< =>\left(x-2\right)\left(x+1\right)=\left(x-2\right)\left(x+2\right)\)
\(< =>\left(x-2\right)\left(x+1-x-2\right)=0\)
\(< =>-1\left(x-2\right)=0\)
\(< =>2-x=0< =>x=2\)
\(2x^3+3x^2-32x=48\)
\(< =>x^2\left(2x+3\right)-16\left(2x+3\right)=0\)
\(< =>\left(x^2-16\right)\left(2x+3\right)=0\)
\(< =>\left(x-4\right)\left(x+4\right)\left(2x+3\right)=0\)
\(< =>\hept{\begin{cases}x=4\\x=-4\\x=-\frac{3}{2}\end{cases}}\)
Xem thêm câu trả lời






















