giúp mình bài tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của đa thưc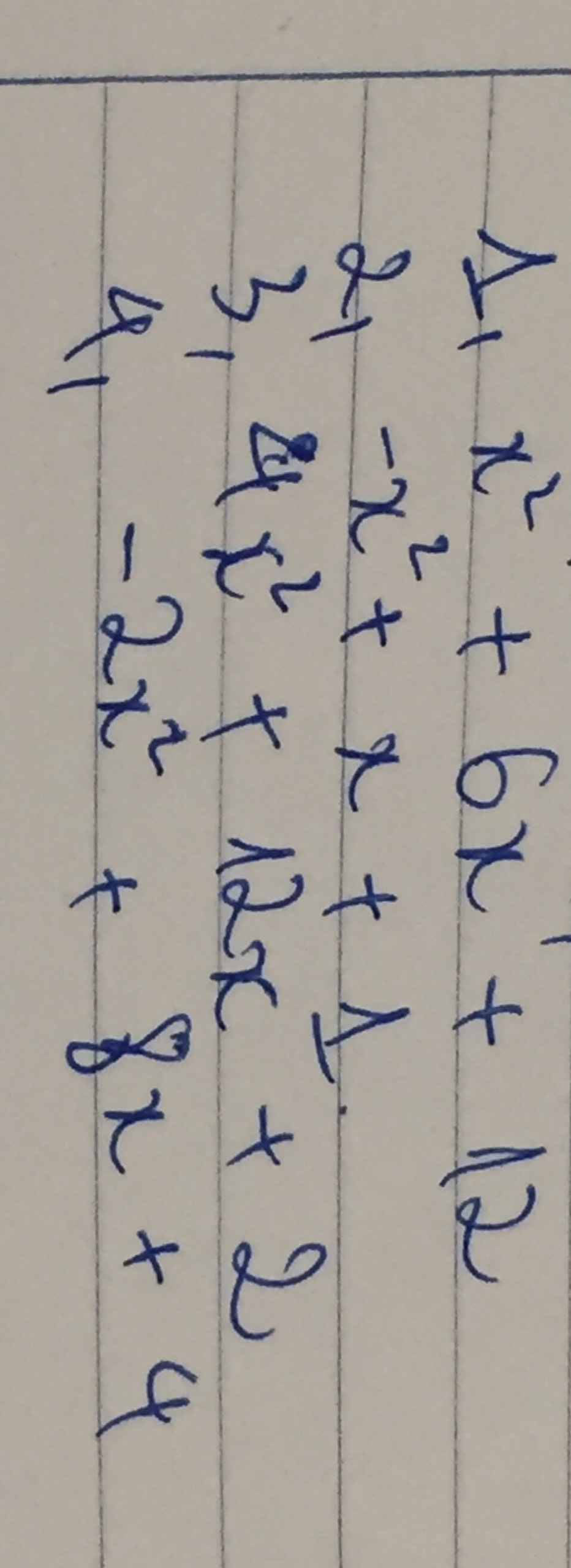

Những câu hỏi liên quan
Tìm giá trị lớn nhất hoặc nhỏ nhất của đa thức
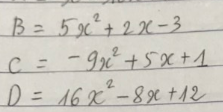
Lời giải:
$B=5x^2+2x-3=5(x^2+\frac{2}{5}x+\frac{1}{5^2})-\frac{16}{5}$
$=5(x+\frac{1}{5})^2-\frac{16}{5}$
$\geq 5.0-\frac{16}{5}=\frac{-16}{5}$
Vậy GTNN của $B$ là $\frac{-16}{5}$. Giá trị này đạt tại $x+\frac{1}{5}=0\Leftrightarrow x=-\frac{1}{5}$
---------------------------------
$C=-9x^2+5x+1=1-(9x^2-5x)$
$=\frac{61}{36}-[(3x)^2-2.3x.\frac{5}{6}+(\frac{5}{6})^2]$
$=\frac{61}{36}-(3x-\frac{5}{6})^2$
$\leq \frac{61}{36}$
Vậy gtln của $C$ là $\frac{61}{36}$. Giá trị này đạt tại $3x-\frac{5}{6}=0\Leftrightarrow x=\frac{5}{18}$
-----------------------
$D=16x^2-8x+12=(4x)^2-2.4x.1+1+11$
$=(4x-1)^2+11\geq 0+11=11$
Vậy gtnn của $D$ là $11$. Giá trị này đạt tại $4x-1=0\Leftrightarrow x=\frac{1}{4}$
Đúng 1
Bình luận (0)
Tìm giá trị nhỏ nhất hoặc giá trị lớn nhất của đa thức sau :
-5x² + x - 7
Tìm giá trị nhỏ nhất hoặc giá trị lớn nhất của đa thức sau :
- 25x² + x + 3
A=...
dăt 5x=y viet cho gon
x=y/5
-A=y^2-y/5+3
=(y-1/10)^2+3-1/100
A=-(y-1/10)^2-299/100
GTLN=-299/100 khi y=1/10
Đúng 0
Bình luận (0)
Các thím giúp mình với, đang cần gấp:
tìm giá trị nhỏ nhất của đa thức: 2(x+10)^2-3
tìm giá trị lớn nhất của đa thức 4-(2x-1)^3
tìm giá trị của biểu thức 7x^2-5
Các thím giúp mình với, đang cần gấp:
tìm giá trị nhỏ nhất của đa thức: 2(x+10)^2-3
tìm giá trị lớn nhất của đa thức 4-(2x-1)^3
tìm giá trị của biểu thức 7x^2-5
Bài 1: tìm x
Bài 2: tìm giá trị lớn nhất hoặc nhỏ nhất của các biểu thức
Mọi người ơi giúp em với :((((
Bài 2:
a: Ta có: \(x^2+x+1\)
\(=x^2+2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{1}{2}\)
b: Ta có: \(-x^2+x+2\)
\(=-\left(x^2-x-2\right)\)
\(=-\left(x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{9}{4}\right)\)
\(=-\left(x-\dfrac{1}{2}\right)^2+\dfrac{9}{4}\le\dfrac{9}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
f: Ta có: \(x^2-2x+y^2-4y+6\)
\(=x^2-2x+1+y^2-4y+4+1\)
\(=\left(x-1\right)^2+\left(y-2\right)^2+1\ge1\forall x,y\)
Dấu '=' xảy ra khi x=1 và y=2
e: Ta có: \(3x^2-6x+1\)
\(=3\left(x^2-2x+\dfrac{1}{3}\right)\)
\(=3\left(x^2-2x+1-\dfrac{2}{3}\right)\)
\(=3\left(x-1\right)^2-2\ge-2\forall x\)
Dấu '=' xảy ra khi x=1
Đúng 1
Bình luận (1)
Bài 1:
a: Ta có: \(\left(x^2-9\right)^2-\left(x-3\right)^2=0\)
\(\Leftrightarrow\left(x-3\right)^2\cdot\left[\left(x+3\right)^2-1\right]=0\)
\(\Leftrightarrow\left(x-3\right)^2\cdot\left(x+2\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-2\\x=-4\end{matrix}\right.\)
b: Ta có: \(x^3-3x+2=0\)
\(\Leftrightarrow x^3-x-2x+2=0\)
\(\Leftrightarrow x\left(x-1\right)\left(x+1\right)-2\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+x-2\right)=0\)
\(\Leftrightarrow\left(x-1\right)^2\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho x,y là các số thưc thỏa mãn x^2+y^2=x+y. Tìm giá trị nhỏ nhất, giá trị lớn nhất của A=x+y
\(x^2+y^2=x+y\\ \Leftrightarrow x^2-x+y^2-y=0\\ \Leftrightarrow\left(x-\dfrac{1}{2}\right)^2+\left(y-\dfrac{1}{2}\right)^2=\dfrac{1}{2}\\ A=x+y=\left(x-\dfrac{1}{2}\right)+\left(y-\dfrac{1}{2}\right)+1\)
Áp dụng Bunhiacopski:
\(\left[\left(x-\dfrac{1}{2}\right)+\left(y-\dfrac{1}{2}\right)\right]^2\le\left(1^2+1^2\right)\left[\left(x-\dfrac{1}{2}\right)^2+\left(y-\dfrac{1}{2}\right)^2\right]=2\cdot\dfrac{1}{2}=1\\ \Leftrightarrow A\le1+1=2\)\(A_{max}=2\Leftrightarrow x=y=1\)
Đúng 2
Bình luận (1)
\(x^2+y^2\ge0\Rightarrow x+y=x^2+y^2\ge0\)
\(A_{min}=0\) khi \(x=y=0\)
Đúng 2
Bình luận (0)
Cách tìm max khác:
Ta có:
$(x-1)^2\geq 0, \forall x\in\mathbb{R}$
$\Rightarrow x^2+1\geq 2x$
Tương tự: $y^2+1\geq 2y$
$\Rightarrow 2(x+y)\leq x^2+y^2+2=x+y+2$
$\Rightarrow x+y\leq 2$ hay $A\leq 2$
Vậy $A_{\max}=2$ khi $x=y=1$
Đúng 1
Bình luận (0)
Cho x,y là các số thưc thỏa mãn x^2+y^2=x+y. Tìm giá trị nhỏ nhất, giá trị lớn nhất của A=x-y
tìm giá trị lớn nhất hoặc giá trị nhỏ nhất :
A= x2 - 6x + 11
giúp mình với
\(A=x^2-6x+11\)
\(=x^2-2x.3+3^2+2\)
\(=\left(x-3\right)^2+2\)
\(\Rightarrow A\ge2\)
\(\Rightarrow MinA=2\)
\(Khi\)\(\left(x-3\right)^2=0\Rightarrow x-3=0\Rightarrow x=3\)
Chúc bn học giỏi nhoa!!!
Đúng 0
Bình luận (0)
bài 1. tìm giá trị lớn nhất của A= -x2+x
bài 2. tìm giá trị lớn nhất của B=x2 -x với -5 bé hơn hoặc bằng x bé hơn hoặc bằng 6
ai giúp mình với, mình tick choo
Bài 1 : A=\(-\left(x^2-2.\frac{1}{2}x+\frac{1}{4}-\frac{1}{4}\right)\)
A=\(-\left(x-\frac{1}{2}\right)^2-\frac{1}{4}< \)hoặc bằng -1/4 Vậy A max =1/4 khi x=1/2
Đúng 0
Bình luận (0)
Dễ thấy hàm số chỉ có 1 điểm cực trị là gtnn nên giá trị lớn nhất là ở 1 trong 2 điểm bị chặn của hàm số thế vào ta được gtln là 30 với x=6 hoặc hoặc -5
Đúng 0
Bình luận (0)























