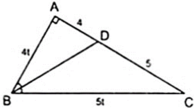
Áp dụng tính chất đường phân giác BD của tam giác

ABC, ta có:

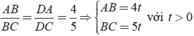 với t > 0

Áp dụng định lý Py – ta – go ta có:

B C 2 = A C 2 + A B 2  hay ( 5 t ) 2 = 9 2 + ( 4 t ) 2 ⇔ ( 3 t ) 2 = 9 2 ⇒ t = 3 (vì t > 0 )

Khi đó: AB = 12cm, BC = 15cm

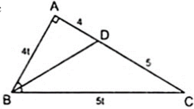
Áp dụng tính chất đường phân giác BD của tam giác ABC, ta có:

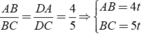với t > 0

Áp dụng định lý Py – ta – go ta có:

Khi đó: AB = 12cm, BC = 15cm

a: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)

Xét ΔBAC có BD là phan giác

=>AD/AB=DC/BC

=>AD/3=DC/5=8/8=1

=>AD=3cm; DC=5cm

b: Xét ΔBAD vuông tại A va ΔBHI vuông tại H có

góc ABD=góc HBI

=>ΔBAD đồng dạng với ΔBHI

=>AD/HI=BA/BH

=>AD*BH=HI*BA
c: góc ADI=góc BIH=góc AID

=>ΔAID cân tại A

Theo định lí Pytago tam giác ABC vuông tại A

\(AC=\sqrt{BC^2-AB^2}=12cm\)

Vì BD là pg \(\dfrac{AB}{BC}=\dfrac{AD}{DC}\Rightarrow\dfrac{DC}{BC}=\dfrac{AD}{AB}\)

Theo tc dãy tỉ số bằng nhau ta có 

\(\dfrac{DC}{BC}=\dfrac{AD}{AB}=\dfrac{12}{24}=\dfrac{1}{2}\Rightarrow DC=\dfrac{15}{2}cm;DA=\dfrac{9}{2}cm\)

a, Xét tam giác ECD và tam giác ACB ta có 

^CED = ^CAB = 90⁰

^C _ chung 

Vậy tam giác ECD ~ tam giác ACB ( g.g )

b, Áp dụng định lí Pytago ta có : 

\(AB^2+AC^2=BC^2\Rightarrow AC^2=BC^2-AB^2=100-36=64\Rightarrow AC=8\)cm 

Do BD là đường phân giác ^B 

\(\Rightarrow\dfrac{AB}{BC}=\dfrac{AD}{DC}\) mà \(DC=AC-AD=8-AD\)

\(\Rightarrow\dfrac{6}{10}=\dfrac{AD}{8-AD}\Rightarrow48-6AD=10AD\Rightarrow16AD=48\Rightarrow AD=3\)cm 

Vậy AD = 3 cm 

c, Ta có : \(\dfrac{S_{ECD}}{S_{ACB}}=\dfrac{\dfrac{1}{2}ED.EC}{\dfrac{1}{2}AC.AB}=\dfrac{ED.EC}{6.8}=\dfrac{ED.EC}{48}\)(*)

\(\dfrac{EC}{AC}=\dfrac{ED}{AB}=\dfrac{CD}{BC}\)( tỉ số đồng dạng ý a ) 

\(\Rightarrow\dfrac{EC}{8}=\dfrac{5}{10}\)( CD = AC - AD = 8 - 3 = 5 cm )

\(\Rightarrow EC=\dfrac{40}{10}=4\) cm (1) 

\(\Rightarrow\dfrac{ED}{AB}=\dfrac{CD}{BC}\Rightarrow ED=\dfrac{AB.CD}{BC}=\dfrac{6.5}{10}=3\)cm (2) 

Thay (1) ; (2) vào (*) ta được :

\(\dfrac{S_{ECD}}{S_{ACB}}=\dfrac{3.4}{48}=\dfrac{12}{48}=\dfrac{1}{4}\)

DB/DC=AB/DC

DB+DC=BC

=>DB=5-20=-15 là sai đề rồi bạn

BC>DC là sai đề rồi bạn

a) Theo hệ thức liên hệ giữa đường cao và hình chiếu , ta có : AH2 = BH . CH

=> CH = AH2/BH = \(\dfrac{162}{25}=10,24\)

BC = BH + CH = 25 + 10,24 = 35,24

- Theo hệ thức liên hệ giữa cạnh góc vuông và hình chéo , ta có :

AB2 = BH.BC

=> AB\(\sqrt{\left(BH.BC\right)}\) 

= \(\sqrt{\left(25.35,24\right)}\)

= \(\sqrt{881=29,68}\)

AC2 = HC.BC

=> AC = \(\sqrt{\left(CH.BC\right)}\)

= \(\sqrt{\left(10,24.35,24\right)=}\sqrt{\left(360,9\right)=18,99}\)