Hai điểm M và N cùng nằm trên 1 nửa mặt phẳng có bờ là đường thẳng xy. Lấy điểm L đối xứng với M qua xy. Gọi I là 1 điểm của xy. Hãy so sánh IM + IN với LN.
Giúp mik với nhanh nhé please!!!!!!
Bài 7: Tính chất đường trung trực của một đoạn thẳng
Cho tam giac ABC có AB<AC lấy E trên cạnh CA sao cho CE=BA các đường trung trực của các đoạn thẳng BE và CE cắt nhau tại I.Chứng minh:tam giác AIB=tam giác CIA.b/ chứng minh : AI là tia phân giác của gốc BAC
2. cho góc XOY bằng 60 độvà điểm A nằm trong góc XOY.vẽ điểm B sao cho OX
là đường trung trực của AB. Vẽ điểm C sao cho OY là đường trung trực của AC
a,chứng minh rằng OB=OC
b,tính số đo góc BOC
a) + Gọi N là giao cảu Ox và AB
+ Gọi G là gaio cảu Oy và AC
+ Kẻ OA -> xét tam giác nob = noa -> 0b = 0a (1) ; ^bon = ^aon
+ Xét tam giac aog = tam giác cog -> oc =oa (2) ; ^aog = ^cog
-> từ (1) và (2) -> ob =oc
+ có ^noa + ^aog = 60
MÀ ^bon = ^aon
^aog = ^goc
-> ^ boc = 60.2 =120
Đúng 0
Bình luận (0)
cho tam giác ABC có góc A=120 độ. hai đường phân giác BD và CE cắt nhau tại I
a, tính số đo góc BIC
b, nối AI kéo dài cắt BC tại F. chứng minh DF vuông góc với FE
giúp mk với na các pạn ![]()
a)\(\Delta ABC:\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
Mà \(\widehat{A}=120^o\Rightarrow\widehat{B}+\widehat{C}=60^o\)
Có \(\widehat{ABD}=\widehat{DBC}=\dfrac{\widehat{ABC}}{2}\) ; \(\widehat{ACE}=\widehat{ECB}=\dfrac{\widehat{ACB}}{2}\)
\(\Rightarrow\widehat{ABD}+\widehat{DBC}+\widehat{ACE}+\widehat{ECB}=60^o\)
\(\Rightarrow2\widehat{DBC}+2\widehat{ECB}=60^o\)
\(\Rightarrow\widehat{DBC}+\widehat{ECB}=30^o\)
\(\Delta BIC:\widehat{DBC}+\widehat{ECB}+\widehat{BIC}=180^o\)
Mà \(\widehat{DBC}+\widehat{ECB}=30^o\) \(\Rightarrow\widehat{BIC}=150^o\)
b)Ta vẽ tia đối Ax là tia đối tia AB
Ta có \(\widehat{BAF}=\widehat{FAC}=\dfrac{\widehat{BAC}}{2}=60^o\) (1)
Thấy\(\widehat{BAC}+\widehat{CAx}=180^o\) (2 góc kề bù)
Mà\(\widehat{BAC}=120^o\Rightarrow\widehat{CAx}=60^o\) (2)
Từ (1) và (2)\(\Rightarrow\) \(\widehat{FAC}=\widehat{CAx}=60^o\)
Nên AC là tia phân giác \(\widehat{FAx}\)
\(\Delta ABF:\)BD là tia phân giác \(\widehat{ABC}\)(tia p/g trong)
AC là tia phân giác \(\widehat{FAx}\) (tia p/g ngoài)
Mà AC,BD,FD đồng quy tại D
Theo t/c 1 đường p/g trong và 2 đường p/g ngoài không kề nó đồng quy tại 1 điểm nên FD là tia phân giác \(\widehat{AFC}\) (cái này là nó được c/m ở SGK bài 32 đó bạn)
Làm tương tự ta cũng được FE là tia phân giác \(\widehat{AFB}\) (bạn sử dụng tam giác AFC ý)
Ta có \(\widehat{AFB}+\widehat{AFC}=180^o\) (2 góc kề bù)
Ta cũng có \(\widehat{BFE}=\widehat{EFA}=\dfrac{\widehat{AFB}}{2}\) ; \(\widehat{AFD}=\widehat{DFC}=\dfrac{\widehat{AFC}}{2}\)
\(\Rightarrow\widehat{BFE}+\widehat{EFA}+\widehat{AFD}+\widehat{DFC}=180^o\)
\(\Rightarrow2\widehat{EFA}+2\widehat{ADF}=180^o\) \(\Rightarrow\widehat{EFA}+\widehat{ADF}=90^o\) \(\Rightarrow\widehat{DFE}=90^o\Rightarrow DF\perp EF\) Chúc bạn học tốt!!!!!
Đúng 1
Bình luận (3)
Cho N nằm trên đường trung trực của đoạn thẳng AB
CMR : NA=NB
gọi d là đường trung trực của đoạn thẳng AB.
d cắt AB tại H
TH1: \(N\equiv H\)
nếu \(N\equiv H\) N cx là trung điểm của AB.
khi đó NA=NB.
TH2: \(N\ne H\)
xét tam giác AHN và tam giác BHN có:
HN: chung
AH=HB.
\(\widehat{AHN}=\widehat{BHN}\)
do đó tam giác AHN= tam giác BHN (c-g-c)
suy ra NA=NB.
Đúng 0
Bình luận (0)
Giải giúp mk vs
Gọi giao điểm của AB và EF là D
Xét tam giác AFB và tam giác AEB có:
+AF=AE (gt)
+BF=BE(gt)
+AB: cạnh chung
=> tam giác AFB=tam giác AEB(c-c-c)
=> góc FBD= góc EBD( góc tương ứng)
Xét tam giác DFB và tam giác DEF:
+DB: cạnh chung
+FB=EB(gt)
+góc FBD= góc EBD( chứng minh trên)
=> tam giác DFB = tam giác DEF(c-g-c)
=> góc FDB= góc EDB ( góc tương ứng)
mà góc FDB+ góc EDB= 180o( kề bù)
=> góc FDB= góc EDB=180o/2=90o
=>AB vuông góc với EF
mà DF=EF(tam giác FDB= tam giác EDB)
Suy ra: AB là đường trung trực của EF(đpcm)
Đúng 0
Bình luận (0)
xét tam giác AFB và tam giác AEB có:
AF=AE
BF=BE
AB: chung
do đó tam giác AFB = tam giác AEB (c-c-c0
\(\Rightarrow\widehat{FAB}=\widehat{BAE}\)
hay AB và đường phân giác của tam giác AEF.
vì tam giác AFE là tam giác cân (AE=AF) nên AB cũng là đường trung trực của tam giác AFE, hay AB là đường trung trực của FE
Đúng 0
Bình luận (0)
bạn làm theo cách này sẽ đúng nè:
gọi giao điểm AB, FE là I
Chứng minh: \(\Delta\)AFI = \(\Delta\)AEI (*)
=> \(\widehat{FAI}\)=\(\widehat{EAI}\)
=>AB là p/g
Từ (*) suy ra AB \(\perp\)EF
=> AB là dg` trung trực của EF
Đúng 0
Bình luận (0)
.jpg)
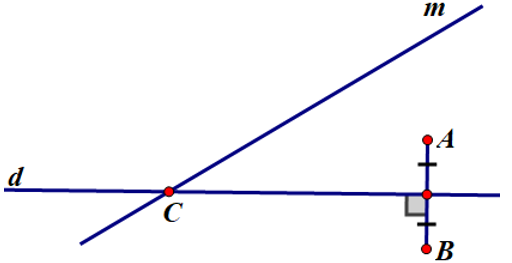
Một con đường quốc lộ cách không xa hai điểm dân cư . Hãy tìm bên đường đó một địa điểm để xây dựng một trạm y tế sao cho trạm y tế này cách đều hai điểm dân cư.
giúp mình nhé
Gọi A và B là hai điểm dân cư ; C là điểm đặt trạm y tế ; m là đường quốc lộ
Vì C cách đều AB nên C thuộc đường trung trực của AB
mà C ∈ xy nên C là giao điểm của xy và đường trung trực (d) của AB.
Gọi 2 điểm dân cư là hai điểm A, B. Để xây dựng trạm y tế ở bên đường cách đều hai điểm dân cư thì trạm y tế đó phải là giao điểm giữa con đường và đường trung trực của AB.
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc C tù . Các đường trung trung của AC,BC cắt nhau tại D và cắt AB lần lượt tại EF . C/m
a,Tam giác BDF = tam giác CDE
b,CD là phân giác góc ECF
cho tam giac ABC can A . canh day nho hon canh ben . đg trung truc cua ac cat đg thang bc tai m .tren tia đoi cua tia am lay diem n sao cho anbm . a)cm:góc amcbac b)cm tam giác abm can...
Đọc tiếp
cho tam giac ABC can A . canh day nho hon canh ben . đg trung truc cua ac cat đg thang bc tai m .tren tia đoi cua tia am lay diem n sao cho an=bm . a)cm:góc amc=bac b)cm tam giác abm =can c) de CM vuong goc CN thi tam giac phai co them đk gì ![]() mình cần gấp .thank truoc
mình cần gấp .thank truoc![]()
Giúp mk vs:
1.So sánh các tích sau:
A1left(dfrac{-42}{50}right).left(dfrac{-119}{80}right)
A2left(dfrac{-7}{13}right).left(dfrac{-4}{65}right).left(dfrac{-8}{31}right)
A3dfrac{-5}{10}.dfrac{-4}{10}.dfrac{-3}{10}......dfrac{3}{10}.dfrac{4}{10}.dfrac{5}{10}
2.Cho hình vẽ sau:
mình vẽ hơi xấu mong các bạn thông cảm
cho biết BAD+...
Đọc tiếp
Giúp mk vs:
1.So sánh các tích sau:
A1=\(\left(\dfrac{-42}{50}\right).\left(\dfrac{-119}{80}\right)\)
A2=\(\left(\dfrac{-7}{13}\right).\left(\dfrac{-4}{65}\right).\left(\dfrac{-8}{31}\right)\)
A3=\(\dfrac{-5}{10}.\dfrac{-4}{10}.\dfrac{-3}{10}......\dfrac{3}{10}.\dfrac{4}{10}.\dfrac{5}{10}\)
2.Cho hình vẽ sau:
mình vẽ hơi xấu mong các bạn thông cảm
cho biết BAD+ADC+DCB+CBA=3600.tính x0
Nhắc trước mọi người tek nhé.Đi qua đây nhớ "bơ"
Cảm ơn trước
Ai còn chưa bt em là ai thì bl em lấy nick em bi
__________Thân____________
Đúng 0
Bình luận (3)