Giải phương trình: 5sin2x - 4sinxcosx + 3cos2x = 2
Những câu hỏi liên quan
Phương trình : \(2sin^2x-5sinxcosx-cos^2x=-2\) tương đương với phương trình nào sau đây :
A . \(3cos2x-5sin2x=5\)
B . \(3cos2x+5sin2x=-5\)
C . \(3cos2x-5sin2x=-5\)
D . \(3cos2x+5sin2x=5\) .
Trình bày bài giải chi tiết rồi ms chọn đáp án nha các bạn .
Phương trình
sin
2
x
-
4
sin
x
cos
x
+
3
cos
2
x
0
có tập nghiệm trùng với nghiệm của phương trình nào sau đây? A.
cos
x
0
B. cotx1 C. tanx3 D. tanx1 hoặc
c
o
t
x
1
3
Đọc tiếp
Phương trình sin 2 x - 4 sin x cos x + 3 cos 2 x = 0 có tập nghiệm trùng với nghiệm của phương trình nào sau đây?
A. cos x = 0
B. cotx=1
C. tanx=3
D. tanx=1 hoặc c o t x = 1 3
Phương trình
sin
2
x
-
4
sin
x
cos
x
+
3
cos
2
x
0
có tập nghiệm trùng với nghiệm của phương trình nào sau đây? A. cot x 1 B. cot x 0 C. cot x 3 D.
tan
x
1
c...
Đọc tiếp
Phương trình sin 2 x - 4 sin x cos x + 3 cos 2 x = 0 có tập nghiệm trùng với nghiệm của phương trình nào sau đây?
A. cot x =1
B. cot x =0
C. cot x =3
D. tan x = 1 c o t x = 1 3
Tìm tất cả các giá trị thực của tham số m để bất phương trình
2
sin
2
x
+
3
cos
2
x
≤
m
.
5
sin
2
x
có nghiệm. A.
m
≠
4...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để bất phương trình 2 sin 2 x + 3 cos 2 x ≤ m . 5 sin 2 x có nghiệm.
A. m ≠ 4
B. m ≥ 4
C. m = 4
D. m < 4
Giải các phương trình sau cos 2 x + 2 sin x . cos x + 5 sin 2 x = 2
cos 2 x + 2 sin x . cos x + 5 sin 2 x = 2
Rõ ràng cosx = 0 không thỏa mãn phương trình. Với cosx ≠ 0, chia hai vế cho cos2x ta được:
1 + 2 tan x + 5 tan 2 x = 2 ( 1 + tan 2 x ) ⇔ 3 tan 2 x + 2 tan x - 1 = 0
Đúng 0
Bình luận (0)
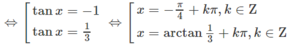
Giải các phương trình sau 5 sin 2 x + 3 cos x + 3 = 0
5 sin 2 x + 3 cos x + 3 = 0 ⇔ 5 ( 1 - cos 2 x ) + 3 cos x + 3 = 0 ⇔ 5 cos 2 x - 3 cos x - 8 = 0 ⇔ ( cos x + 1 ) ( 5 cos x - 8 ) = 0 ⇔ cos x = - 1 ⇔ x = ( 2 k + 1 ) π , k ∈ Z
Đúng 0
Bình luận (0)
Giải phương trình sau: 3cos2x – 5cosx + 2 = 0
3cos2x - 5 cos x + 2 = 0
Đặt cos x = t với điều kiện -1 ≤ t ≤ 1 (*),
ta được phương trình bậc hai theo t:
3t2 - 5t + 2 = 0(1)
Δ = (-5)2 - 4.3.2 = 1
Phương trình (1)có hai nghiệm là:
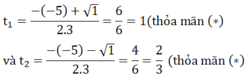
Ta có:
cosx = 1 ⇔ cosx = cos0
⇔ x = k2π, k ∈ Z
cosx = 2/3 ⇔ x = ± arccos 2/3 + k2π, k ∈ Z
Đúng 0
Bình luận (0)
Giải các phương trình sau :
a) 3sin^2x-4sinxcosx+5cos^2x2
b) 25sin^2x+15sin2x+9cos^225
c) sinx + cosx 1
d) 3cos2x - 4sin2x 1
f) 4sin^2x-6cos^2x0
g) 5sin2x-6cos^2x13
h) sinxsqrt{3}cosx
i) sin^4x+cos^4left(x+frac{pi}{4}right)frac{1}{4}
j)tanx+2cotx-30
k) tan^25xfrac{1}{3}
m) sin^4x-cos^4xcosx-2
Đọc tiếp
Giải các phương trình sau :
a) \(3sin^2x-4sinxcosx+5cos^2x=2\)
b) \(25sin^2x+15sin2x+9cos^2=25\)
c) sinx + cosx =1
d) 3cos2x - 4sin2x =1
f) \(4sin^2x-6cos^2x=0\)
g) \(5sin2x-6cos^2x=13\)
h) \(sinx=\sqrt{3}cosx\)
i) \(sin^4x+cos^4\left(x+\frac{\pi}{4}\right)=\frac{1}{4}\)
j)\(tanx+2cotx-3=0\)
k) \(tan^25x=\frac{1}{3}\)
m) \(sin^4x-cos^4x=cosx-2\)
a)
PT $\Leftrightarrow \sin ^2x-4\sin x\cos x+3\cos ^2x+2(\sin ^2x+\cos ^2x)=2$
$\Leftrightarrow \sin ^2x-4\sin x\cos x+3\cos ^2x=0$
$\Leftrightarrow (\sin x-3\cos x)(\sin x-\cos x)=0$
Nếu $\sin x-3\cos x=0$. Dễ thấy $\sin x, \cos x\neq 0$ nên $\tan x=\frac{\sin x}{\cos x}=3$
$\Rightarrow x=k\pi +\tan ^{-1}(3)$ với $k$ nguyên
Nếu $\sin x=\cos x$ thì tương tự ta có $\tan x=1\Rightarrow x=\pi (k+\frac{1}{4})$ với $k$ nguyên
Đúng 0
Bình luận (0)
b)
PT $\Leftrightarrow 25(\sin ^2x+\cos ^2x)+30\sin x\cos x-16\cos ^2x=25$
$\Leftrightarrow 30\sin x\cos x-16\cos ^2x=0$
$\Leftrightarrow \cos x(15\sin x-8\cos x)=0$
Nếu $\cos x=0\Rightarrow x=\pi (k+\frac{1}{2})$ với $k$ nguyên
Nếu $15\sin x-8\cos x=0$
Dễ thấy $\cos x\neq 0$ nên suy ra $\tan x=\frac{\sin x}{\cos x}=\frac{8}{15}$
$\Rightarrow x=k\pi +\tan ^{-1}(\frac{8}{15})$ với $k$ nguyên
Đúng 0
Bình luận (0)
c) \(\left\{\begin{matrix} \sin x+\cos x=1\\ \sin ^2x+\cos ^2x=1\end{matrix}\right.\Rightarrow \left\{\begin{matrix} (\sin x+\cos x)^2=1\\ \sin ^2x+\cos ^2x=1\end{matrix}\right.\)
\(\Rightarrow 2\sin x\cos x=0\Leftrightarrow \sin 2x=0\Rightarrow x=\frac{k}{2}\pi\) với $k$ nguyên.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải các phương trình sau 3 cos 2 x - 2 sin x + 2 = 0
3 cos 2 x - 2 sin x + 2 = 0 ⇔ 3 ( 1 - sin 2 x ) - 2 sin x + 2 = 0 ⇔ 3 sin 2 x + 2 sin x - 5 = 0 ⇔ ( sin x - 1 ) ( 3 sin x + 5 ) = 0 ⇔ sin x = 1 ⇔ x = π / 2 + k 2 π , k ∈ Z
Đúng 0
Bình luận (0)
Giải phương trình
3
cos
2
x
+
sin
2
x
+
2
sin
2
x
-
π
6
2
2
Đọc tiếp
Giải phương trình 3 cos 2 x + sin 2 x + 2 sin 2 x - π 6 = 2 2
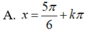
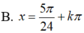
