Cho đa thức A(x) = x2 – 2x + 1 .Trong các số 0; 1; -1 ; -2 , số nào là nghiệm của đa thức A(x) ? Vì sao ?
giup em vs a
Trong các số cho sau, với mỗi đa thức, số nào là nghiệm của đa thức ?
a) P(x) = 2x + 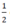 |
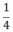 |
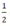 |
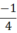 |
| b) Q(x) = x2 – 2x -3 | 3 | 1 | -1 |
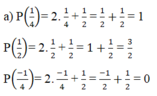
Vậy x = 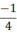 là nghiệm của đa thức P(x) = 2x +
là nghiệm của đa thức P(x) = 2x + 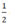
b) Q(3) = 32 – 2.3 – 3 = 9 – 6 – 3 = 0
Q(1) = 12 – 2.1 – 3 = 1 – 2 – 3 = - 4
Q(-1) = (-1)2 – 2.(-1) – 3 = 1 + 2 – 3 = 0
Vậy x = 3 và x = - 1 là nghiệm của đa thức Q(x) = x2 – 2x – 3
Cho các đa thức sau f ( x ) = - x - 3 , g ( x ) = x 2 + 3 , h ( x ) = x 2 - 9 , k ( x ) = x 2 - 2 x - 15 . Số các đa thức nhận x = -3 là nghiệm trong các đa thức trên là:
A. 1
B. 2
C. 3
D. 4
Chọn C
Ta có
f(-3) = - (-3) - 3 = 0,
g(-3) = (-3)2 + 3 = 12,
h(-3) = (-3)2 - 9 = 0,
k(-3) = (-3)2-2.(-3) - 15 = 0
Nên x = -3 là nghiệm của f(x), g(x), k(x).
11.Cho đa thức P(x) = a.x7+ b.x3+ c.x – 5, trong đó a, b, c là các hằng số nào đó. Biết rằngP(-7) = 7. Tính giá trị của P(7).
12.Cho đa thức P(x) và Q(x) là các đa thức thỏa mãn:
P(x) + Q(x) = x3+ x2– 4x + 2 và P(x) – Q(x) = x3– x2+ 2x – 2.
a) Xác định đa thức P(x) và Q(x).
b) Tìm nghiệm của đa thức P(x) và Q(x). c. Tính giá trị của P(x) và Q(x) biết |x - |x/2-|x –1||| = x – 2.
13.Biết rằng P(x) = n.xn+4 + 3.x4-n– 2x3+ 4x – 5 và Q(x) = 3.xn+4– x4+ x3+ 2nx2+ x – 2 là các đa thức với n là một số nguyên. Xác định n sao cho P(x) – Q(x) là một đa thức bậc 5 và có 6 hạng tử.
9. Tính giá trị của P = 2y4+ 7x – 2z4 biết x, y, z nguyên và thỏa mãn (x2+ 1)2+ (y-z)2 = 100.
cho rút lại lời vừa ns khi coi hết đề:>
Bài 3: Cho các đa thức f(x) = 2x(x2 - 3) - 4( 1- 2x) + x2 (x -2 )+ (5x + 3)
g(x) = -3 (1 - x 2) - 2 ( x2 - 2x -1)
a) Thu gọn các đa thức trên và sắp xếp theo luỹ thừa giảm dần của biến x.
b) Tính h(x) = f(x) - g(x) và tìm nghiệm của đa thức h(x
\(a)\)
\(f\left(x\right)=2x.\left(x^2-3\right)-4.\left(1-2x\right)+x^2.\left(x-2\right)+\left(5x+3\right)\)\(=2x^3-6x-4+8x+x^3-2x^2+5x+3=3x^3+7x-1-2x^2=3x^3-2x^2+7x-1\)\(g\left(x\right)=-3.\left(1-x^2\right)-2.\left(x^2-2x-1\right)=-3+3x^2-2x^2+4x+2=-1+x^2+4x=x^2+4x-1\)
\(b)\)
\(h\left(x\right)=f\left(x\right)-g\left(x\right)=\left(3x^3-2x^2+7x-1\right)-\left(-1+x^2+4x\right)=x^2+4x-1=3x^3-2x^2+7x-1+1-x^2-4x=3x^3-3x^2+3x\)
\(\text{Xét}:\)
\(3x^3-3x^2+3x=0\)
\(\rightarrow3x.\left(x^2-x+1\right)=0\)
\(\rightarrow x.\left(x^2-x+1\right)=0\)
\(\rightarrow\orbr{\begin{cases}3x.\left(x^2-x+1\right)=0\\x.\left(x^2-x+1\right)=0\end{cases}}\) \(\rightarrow\orbr{\begin{cases}x=0\\x^2-x+1=0\end{cases}}\)
\(\rightarrow\orbr{\begin{cases}x=0\\x\notinℝ\end{cases}}\) \(\rightarrow x=0\)
\(\text{Vậy nghiệm của}\)\(h\left(x\right)\)\(\text{là}:\)\(0\)
Trong số các số bên phải của các đa thức sau, số nào là nghiệm của đa thức bên trái nó?
Q x = x 2 + x ; - 1 0 1 2 1
Q(x) = x2 + x
Q(-1) = (-1)2 + (-1) = 1 – 1 = 0
Q(0) = 02 + 0 = 0 + 0 = 0
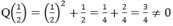
Q(1) = 12 + 1 = 1 + 1 = 2 ≠ 0.
Vậy -1 và 0 là nghiệm của Q(x).
Cho hai đa thức A(x) = 3(x2+2-4x)-2x(x-2)+17 và B(x) = 3x2-7x+3-3(x2-2x+4) a) Thu gọn A(x),B(x). Sắp xếp các đa thức theo luỹ thừa giảm dần của biến. Tìm hệ số cai nhất, hệ số tự do của hai đa thức đó b) Tìm N(x) sao cho N(x)-B(x)=A(x) và M(x) sao cho A(x)-M(x)=B(x).
`@` `\text {Ans}`
`\downarrow`
`a)`
`A(x) = \(3(x^2+2-4x)-2x(x-2)+17\)
`= 3x^2 + 6 - 12x - 2x^2 + 4x + 17`
`= x^2 - 8x + 23`
Hệ số cao nhất: `1`
Hệ số tự do: `23`
`B(x) = \(3x^2-7x+3-3(x^2-2x+4)\)
`=3x^2 - 7x + 3 - 3x^2 + 6x - 12`
`= -x - 9`
Hệ số cao nhất: `-1`
Hệ số tự do: `-9`
`b)`
`N(x) - B(x) = A(x)`
`=> N(x) = A(x) + B(x)`
`=> N(x) = (x^2 - 8x + 23)+(-x-9)`
`= x^2 - 8x + 23 - x - 9`
`= x^2 - 9x + 14`
`A(x) - M(x) = B(x)`
`=> M(x) = A(x) - B(x)`
`=> M(x) = (x^2 - 8x + 23) - (-x - 9)`
`= x^2 - 8x + 23 + x+9`
`= x^2 - 7x +32`
a)A(x) = 3(x^2 + 2 - 4x) - 2x(x - 2) + 17
= 3x^2 + 6 - 12x - 2x^2 + 4x + 17
= x^2 - 2x + 23
b)B(x) = 3x^2 - 7x + 3 - 3(x^2 - 2x + 4)
= 3x^2 - 7x + 3 - 3x^2 + 6x - 12
= -x + -9
A(x) = x^2 - 2x + 23
B(x) = -x - 9
Hệ số cao nhất của đa thức A(x) là 1, hệ số tự do của A(x) là 23.
Hệ số cao nhất của đa thức B(x) là -1, hệ số tự do của B(x) là -9.
b)
N(x) - B(x) = A(x)
N(x) - (-x - 9) = x^2 - 2x + 23
N(x) + x + 9 = x^2 - 2x + 23
N(x) = x^2 - 3x + 14
Vậy, N(x) = x^2 - 3x + 14.
A(x) - M(x) = B(x)
x^2 - 2x + 23 - M(x) = -x - 9
x^2 - 2x + x + 9 + 23 = M(x)
x^2 - x + 32 = M(x)
Vậy, M(x) = x^2 - x + 32.
a: A(x)=3x^2+6-12x-2x^2+4x+17
=x^2-8x+23
B(x)=3x^2-7x+3-3x^2+6x-12=-x-9
Hệ số cao nhất của A(x) là 1
Hệ số tự do của A(x) là 23
Hệ số cao nhất của B(x) là -1
Hệ số tự do của B(x) là -9
b: N(x)=A(x)+B(x)
=x^2-8x+23-x-9
=x^2-9x+14
M(x)=A(x)-B(x)
=x^2-8x+23+x+9
=x^2-7x+32
1, Đa thức f(x) khi chia cho x+1 dư 4 khi chia x2+1 dư 2x+3. Tìm đa thức dư khi chia f(x) cho (x+1)(x2+1)
2, Cho P=(a+b)(b+c)(c+a)-abc với a,b,c là các số nguyên. CMR nếu a+b+c chia hết cho 4 thì P chia hết cho 4
2) Ta có đẳng thức sau: \(\left(a+b\right)\left(b+c\right)\left(c+a\right)=\left(a+b+c\right)\left(ab+bc+ca\right)-abc\)
Chứng minh thì bạn chỉ cần bung 2 vế ra là được.
\(\Rightarrow P=\left(a+b+c\right)\left(ab+bc+ca\right)-2abc\)
Do \(a+b+c⋮4\) nên ta chỉ cần chứng minh \(abc⋮2\) là xong. Thật vậy, nếu cả 3 số a, b,c đều không chia hết cho 2 thì \(a+b+c\) lẻ, vô lí vì \(a+b+c⋮4\). Do đó 1 trong 3 số a, b, c phải chia hết cho 2, suy ra \(abc⋮2\).
Do đó \(P⋮4\)
Kiểm tra xem 1 số có phải lả nghiệm của đa thức 1 biến hay không ?
a, Cho đa thức: f(x) = 2x^2 + x - 3. Trong các số 1; -1; 2; 3 số nào là nghiệm của đa thức f(x) ?
b, Cho đa thức: g(x) = 5x^2 + 2x - 3. Trong các số 1; -1 số nào là nghiệm của đa thức g(x) ?
Cho đa thức M(x)=x2 - 4x + 4
a,Tính giá trị của đa thức tại x = 1 ;x = 2; x =3 và x = -1
b,Trong các số 1;2;3 và -1 ,số nào là nghiệm của đa thức M(x)
a. Thay x = 1 vào đa thức ta có:
\(1^2-4.1+4=1\)
Thay x = 2 vào đa thức ta có
\(2^2-4.2+4=0\)
Thay x = 3 vào đa thức ta có:
\(3^2-4.3+4=1\)
Thay x = -1 vào đa thức ta có:
\(\left(-1\right)^2-4.\left(-1\right)+4=9\)
b. Trong các số trên 2 là nghiệm của đa thức M(x)
a, M(\(x\)) = \(x^2\) - 4\(x\) + 4
M(1) = 12 - 4.1 + 4 = 1
M(2) = 22 - 4.2 + 4 = 0
M(3) = 32 - 4.3 + 4 = 1
M(-1) = (-1)2 - 4.(-1) + 4 = 9
b, Trong các số 1; 2; 3 và -1 thì 2 là nghiệm của M(\(x\)) vì M(2) = 0
a. Thay x = 1 vào đa thức ta có:
Thay x = 2 vào đa thức ta có
Thay x = 3 vào đa thức ta có:
Thay x = -1 vào đa thức ta có:
b. Trong các số trên 2 là nghiệm của đa thức M(x)
Biểu diễn đa thức A = B.Q + R trong đó Q, R là đa thức chia và đa thức dư trong phép chia A cho B.
a) A = x 3 - 4 x 2 - 12x và B = x + 2;
b) A = x 3 - 3 x 2 + 39x - 6 và B = x 2 - 5x +1;
c) A = 3 x 3 + 7 x 2 - 7x + 3 - 3 và B = 3 x 2 - 2x - 1.
a) A = ( x 2 – 6x)B.
b) A = (-x – 8)B + 2
c) A = (x + 3)B + 6.