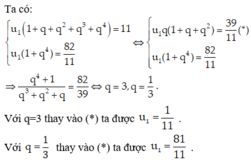2U1+u3-u5=2 U3+u6=11 Tìm số hạng đầu d và u1 Tính s10

Những câu hỏi liên quan
Tính số hạng đầu
u
1
và công sai d của cấp số cộng
(
u
n
)
biết
u
1
+
u
5
-...
Đọc tiếp
Tính số hạng đầu u 1 và công sai d của cấp số cộng ( u n ) biết u 1 + u 5 - u 3 = 10 u 1 + u 6 = 7
Ai đó làm ơn giúp mình với ạ, mình cảm ơn rất nhiều 1.Cho cấp số nhân(Un). Tìm U1 và q. Biết rằng a. U1 + u6= 165; u3 + u4=60 2. Tìm số hạng đầu và công bội của cấp số nhân, biết a. U4- u2= 72; U5- u3=144 b. u1- u3+u5=65;u1+u7=325 c. u3+u5=90; u2-u6=240 d. u1+u2+u3=14; u1.u2.u3=64
Để tìm U1 và q, ta sử dụng hệ phương trình sau:
U1 + U6 = 165U3 + U4 = 60Đầu tiên, ta sử dụng phương trình thứ hai để tìm U3: U3 = 60 - U4
Sau đó, thay giá trị của U3 vào phương trình thứ nhất: U1 + U6 = 165 U1 + (U3 + 3q) = 165 U1 + (60 - U4 + 3q) = 165 U1 - U4 + 3q = 105 (1)
Tiếp theo, ta sử dụng phương trình thứ nhất để tìm U6: U6 = 165 - U1
Thay giá trị của U6 vào phương trình thứ hai: U3 + U4 = 60 (60 - U4) + U4 = 60 60 = 60 (2)
Từ phương trình (2), ta thấy rằng phương trình không chứa U4, do đó không thể giải ra giá trị của U4. Vì vậy, không thể tìm được giá trị cụ thể của U1 và q chỉ từ hai phương trình đã cho.
Để tìm số hạng đầu và công bội của cấp số nhân, ta sử dụng các phương trình đã cho:
a. U4 - U2 = 72 U5 - U3 = 144
Đầu tiên, ta sử dụng phương trình thứ nhất để tìm U4: U4 = U2 + 72
Sau đó, thay giá trị của U4 vào phương trình thứ hai: U5 - U3 = 144 (U2 + 2q) - U3 = 144 U2 - U3 + 2q = 144 (3)
Từ phương trình (3), ta thấy rằng phương trình không chứa U2, do đó không thể giải ra giá trị của U2 và q chỉ từ hai phương trình đã cho.
b. U1 - U3 + U5 = 65 U1 + U7 = 325
Đầu tiên, ta sử dụng phương trình thứ hai để tìm U7: U7 = 325 - U1
Sau đó, thay giá trị của U7 vào phương trình thứ nhất: U1 - U3 + U5 = 65 U1 - U3 + (U1 + 6q) = 65 2U1 - U3 + 6q = 65 (4)
Từ phương trình (4), ta thấy rằng phương trình không chứa U3, do đó không thể giải ra giá trị của U1 và q chỉ từ hai phương trình đã cho.
c. U3 + U5 = 90 U2 - U6 = 240
Đầu tiên, ta sử dụng phương trình thứ hai để tìm U6: U6 = U2 - 240
Sau đó, thay giá trị của U6 vào phương trình thứ nhất: U3 + U5 = 90 U3 + (U2 - 240 + 4q) = 90 U3 + U2 - 240 + 4q = 90 U3 + U2 + 4q = 330 (5)
Từ phương trình (5), ta thấy rằng phương trình không chứa U2, do đó không thể giải ra giá trị của U2 và q chỉ từ hai phương trình đã cho.
d. U1 + U2 + U3 = 14 U1 * U2 * U3 = 64
Đầu tiên, ta sử dụng phương trình thứ nhất để tìm U3: U3 = 14 - U1 - U2
Sau đó, thay giá trị của U3 vào phương trình thứ hai: U1 * U2 * (14 - U1 - U2) = 64
Phương trình này có dạng bậc ba và không thể giải ra giá trị cụ thể của U1 và U2 chỉ từ hai phương trình đã cho.
Tóm lại, không thể tìm được giá trị cụ thể của số hạng đầu và công bội của cấp số nhân chỉ từ các phương trình đã cho.
Đúng 0
Bình luận (0)
Tìm số hạng đầu u1 của cấp số nhân
(
u
n
)
biết rằng
u
1
+
u
2
+
u
3
168
và...
Đọc tiếp
Tìm số hạng đầu u1 của cấp số nhân ( u n ) biết rằng u 1 + u 2 + u 3 = 168 và u 4 + u 5 + u 6 = 21
A. u 1 = 24
B. u 1 = 1344 11
C. u 1 = 96
D. u 1 = 217 3
Chọn C.
Công thức tổng quát của CSN có số hạng đầu là u1 và công bội q
u n = u 1 . q n - 1
Cách giải:
Gọi số hạng đầu và công bội của CSN lần lượt là u 1 , q
Theo đề bài ta có hệ phương trình:
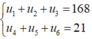
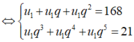
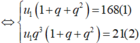
Lây (2) chia cho (1) ta được:
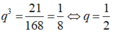
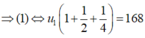
![]()
Đúng 0
Bình luận (0)
Tìm số hạng đầu
u
1
của cấp số nhân
u
n
biết rằng
u
1
+
u
2
+
u
3
168
v
à
u
4
+
u
5
+
u
6...
Đọc tiếp
Tìm số hạng đầu u 1 của cấp số nhân u n biết rằng u 1 + u 2 + u 3 = 168 v à u 4 + u 5 + u 6 = 21.
A. u 1 = 24
B. u 1 = 1344 11
C. u 1 = 96
D. u 1 = 217 3
Tìm số hạng đầu và công sai của các cấp số cộng sau, biết:
u
1
-
u
3
+
u
5
...
Đọc tiếp
Tìm số hạng đầu và công sai của các cấp số cộng sau, biết: u 1 - u 3 + u 5 = 10 u 1 + u 6 = 7
Ta có : u3 = u1 + 2d ;
u5 = u1 + 4d ;
u6 = u1 + 5d
Theo đề bài ta có :
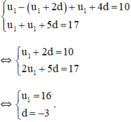
Đúng 0
Bình luận (0)
I. Cho cấp số cộng (un) thỏa mãn u2 + u3 + u5 17 và u6 - 2u1 9. Tìm u1 và công sai của cấp số cộng đã cho.
II. Cho hình chóp S.ABCD có đáy là hình thang ABCD, đáy lớn AD và AD 2BC. Gọi O là giao điểm của AC và BD; G là trọng tâm tam giác △SBD.
1. Chứng minh AD // (SBC)
2. Chứng minh OG // (SAB)
III.
1. Tìm số hạng không chứa x trong khai triển left(x+dfrac{2}{x}right)^8.
2. Một tổ có 9 học sinh gồm 5 học sinh nam và 4 học sinh nữ, trong đó có 2 học sinh nam tên Phúc và Đức. Xếp ngẫu nhi...
Đọc tiếp
I. Cho cấp số cộng (un) thỏa mãn u2 + u3 + u5 = 17 và u6 - 2u1 = 9. Tìm u1 và công sai của cấp số cộng đã cho.
II. Cho hình chóp S.ABCD có đáy là hình thang ABCD, đáy lớn AD và AD = 2BC. Gọi O là giao điểm của AC và BD; G là trọng tâm tam giác △SBD.
1. Chứng minh AD // (SBC)
2. Chứng minh OG // (SAB)
III.
1. Tìm số hạng không chứa x trong khai triển \(\left(x+\dfrac{2}{x}\right)^8\).
2. Một tổ có 9 học sinh gồm 5 học sinh nam và 4 học sinh nữ, trong đó có 2 học sinh nam tên Phúc và Đức. Xếp ngẫu nhiên 9 học sinh trên thành một hàng ngang. Có bao nhiêu cách xếp sao cho hai học sinh Phúc và Đức luôn đứng cạnh nhau, đồng thời các học sinh nam còn lại không đứng cạnh nhau và cũng không đứng cạnh Đức và Phúc?
Giải giúp mình nhé. Help!!!
Cho cấp số nhân
u
n
có số hạng đầu
u
1
2
và số hạng thứ ba là
u
3
18
. Giá trị của
u
6
bằng A. 486 hoặc
-
486 B. 486 C. 972 D. 42
Đọc tiếp
Cho cấp số nhân u n có số hạng đầu u 1 = 2 và số hạng thứ ba là u 3 = 18 . Giá trị của u 6 bằng
A. 486 hoặc - 486
B. 486
C. 972
D. 42
Đáp án A

Chú ý khi giải:
Nhiều HS sẽ chọn nhầm đáp án D vì đọc không kĩ đề thành cấp số “cộng”.
Nhiều em khác lại chọn nhầm B vì quên mất trường hợp q = -3
Đúng 0
Bình luận (0)
Cho cấp số nhân
(
u
n
)
có số hạng đầu
u
1
2
và số hạng thứ ba là
u
3
18
. Giá trị của
u
6
bằ...
Đọc tiếp
Cho cấp số nhân ( u n ) có số hạng đầu u 1 = 2 và số hạng thứ ba là u 3 = 18 . Giá trị của u 6 bằng
A. 486 hoặc -486
B. 486
C. 972
D. 42
Phương pháp:
- Tính công bội q, từ đó suy ra u 6
- Sử dụng công thức u n = u 1 q n - 1
Cách giải:
Ta có: u 3 = u 1 q 2 ⇔ q = ± 3
Vậy với q = 3 thì u 6 = u 1 . q 5 = 486
Với q = - 3 thì u 6 = u 1 . q 5 = - 486
Chọn: A
Đúng 0
Bình luận (0)
1) Tìm số hạng đầu u1 và công bội q của Cấp Số Nhân (Un)
a) Biết u2-10, u3-20
b) Biết u32, u61/4
c) Biết{ u1-u3-9; u3-u5-36}
2)Tìm S8 của Cấp Số Nhân (Un) biết:
{u4-u224; u3-u112}
3) Cho Cấp Số Nhân(Un) với công bội q :
a) biết u14; q -2. Tính u10 và S15
4) Chứng minh : Dãy số sau là cấp số nhân
a) Dãy số có số hạng tổng quát : Un 5x(1/2)^2n-1
5) Cho q1/3,S5 121.Tìm u1
6) Cho Cấp Số Nhân có u24 và u49. Tính giá trị của u3.
Đọc tiếp
1) Tìm số hạng đầu u1 và công bội q của Cấp Số Nhân (Un)
a) Biết u2=-10, u3=-20
b) Biết u3=2, u6=1/4
c) Biết{ u1-u3=-9; u3-u5=-36}
2)Tìm S8 của Cấp Số Nhân (Un) biết:
{u4-u2=24; u3-u1=12}
3) Cho Cấp Số Nhân(Un) với công bội q :
a) biết u1=4; q =-2. Tính u10 và S15
4) Chứng minh : Dãy số sau là cấp số nhân
a) Dãy số có số hạng tổng quát : Un= 5x(1/2)^2n-1
5) Cho q=1/3,S5 =121.Tìm u1
6) Cho Cấp Số Nhân có u2=4 và u4=9. Tính giá trị của u3.
1.
\(\left\{{}\begin{matrix}u_2=u_1q=-10\\u_3=u_1q^2=-20\end{matrix}\right.\) \(\Rightarrow\frac{u_1q^2}{u_1q}=\frac{-20}{-10}\Rightarrow q=2\)
\(\Rightarrow u_1=\frac{-10}{q}=-5\)
b/ \(\left\{{}\begin{matrix}u_1q^2=2\\u_1q^5=\frac{1}{4}\end{matrix}\right.\) \(\Rightarrow q^3=\frac{1}{8}\Rightarrow q=\frac{1}{2}\)
\(\Rightarrow u_1=\frac{2}{q^2}=8\)
c/ \(\left\{{}\begin{matrix}u_1-u_1q^2=-9\\u_1q^2-u_1q^4=-36\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1\left(1-q^2\right)=-9\\u_1q^2\left(1-q^2\right)=-36\end{matrix}\right.\)
\(\Leftrightarrow\frac{u_1q^2\left(1-q^2\right)}{u_1\left(1-q^2\right)}=\frac{-36}{-9}\Rightarrow q^2=4\Rightarrow\left[{}\begin{matrix}q=2\\q=-2\end{matrix}\right.\)
\(\Rightarrow u_1=\frac{-9}{1-q^2}=\frac{-9}{-3}=3\)
Đúng 0
Bình luận (0)
Bài 2:
\(\left\{{}\begin{matrix}u_1q^3-u_1q=24\\u_1q^2-u_1=12\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1q\left(q^2-1\right)=24\\u_1\left(q^2-1\right)=12\end{matrix}\right.\)
\(\Leftrightarrow\frac{u_1q\left(q^2-1\right)}{u_1\left(q^2-1\right)}=\frac{24}{12}\Rightarrow q=2\Rightarrow u_1=\frac{12}{q^2-1}=4\)
\(\Rightarrow S_8=u_1.\frac{q^8-1}{q-1}=4\left(2^8-1\right)=...\)
Câu 3:
\(u_{10}=u_1q^9=4\left(-2\right)^9=-2^{11}\)
\(S_{15}=u_1.\frac{q^{15}-1}{q-1}=4.\frac{\left(-2\right)^{15}-1}{-3}=\frac{3}{4}\left(2^{15}+1\right)\)
Đúng 1
Bình luận (0)
Bài 4:
\(u_n=5.\left(\frac{1}{2}\right)^{2n-1}=10.\left(\frac{1}{2}\right)^{2n}=10\left(\frac{1}{4}\right)^n\)
Là cấp số nhân với \(u_1=10\) và công bội \(q=\frac{1}{4}\)
Bài 5:
\(S_5=u_1.\frac{q^4-1}{q-1}=u_1.\frac{\left(\frac{1}{3}\right)^4-1}{\frac{1}{3}-1}=\frac{121}{81}u_1\)
\(\Rightarrow u_1=\frac{81}{121}S_5=81\)
Bài 6:
\(\left\{{}\begin{matrix}u_1q=4\\u_1q^3=9\end{matrix}\right.\) \(\Rightarrow\left(u_1q^2\right)^2=36\Rightarrow\left[{}\begin{matrix}u_1q^2=6\\u_1q^2=-6\end{matrix}\right.\)
Mà \(u_3=u_1q^2\Rightarrow u_3=\pm6\)
Đúng 0
Bình luận (0)
Cho cấp số nhân (un) có các số hạng khác không, tìm
u
1
biết:
u
1
+
u
2
+
u
3
+
u
4...
Đọc tiếp
Cho cấp số nhân (un) có các số hạng khác không, tìm u 1 biết:
u 1 + u 2 + u 3 + u 4 + u 5 = 11 u 1 + u 5 = 82 11
A. 1 11
B. 81 11
C. 21 11
D. Tất cả sai