tìm đkxd của pt

Những câu hỏi liên quan
Tìm đkxd của pt
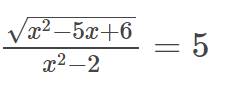
ĐKXĐ: x^2-5x+6>=0 và x^2-2<>0
=>(x>=3 hoặc x<=2) và (x<>căn 2 và x<>-căn 2)
=>x>=3 hoặc \(\left\{{}\begin{matrix}x< =2\\x\notin\left\{\sqrt{2};-\sqrt{2}\right\}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
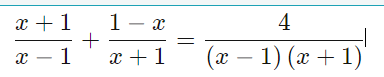
tìm đkxd và giải pt .hứa vote nhanh ạ.
\(\dfrac{x+1}{x-1}+\dfrac{1-x}{x+1}=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\left(ĐKXĐ:x\ne1;x\ne-1\right)\)
\(\Leftrightarrow\left(x+1\right)\left(x+1\right)+\left(1-x\right)\left(x-1\right)=4\)
\(\Leftrightarrow x^2+x+x+1+x-1-x^2+x=4\)
\(\Leftrightarrow x^2-x^2+x+x+x+x-4+1-1=0\)
\(\Leftrightarrow4x-4=0\)
\(\Leftrightarrow4x=4\)
\(\Leftrightarrow x=1\left(loại\right)\)
Vậy \(S=\varnothing\)
Đúng 2
Bình luận (0)
\(\dfrac{x+1}{x-1}+\dfrac{1-x}{x+1}=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\)
⇔ \(\dfrac{\left(x+1\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}+\dfrac{\left(1-x\right)\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\)
⇔ \(\dfrac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}+\dfrac{-\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\)
⇔ \(\dfrac{\left(x+1\right)^2-\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\)
⇔ \(\dfrac{\left(x+1+x-1\right)\left(x+1-x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\)
⇔ \(\dfrac{2x.2}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\)
⇔ \(\dfrac{4x}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\)
⇒ \(4x=4\)
⇔ \(x=1\) (ko thỏa mãn dktc)
Vậy phương trình vô nghiệm
Đúng 2
Bình luận (0)
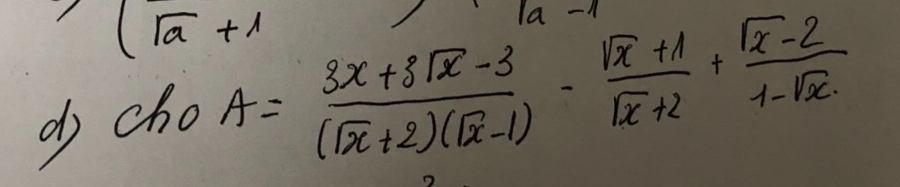
a) tìm đkxd của A
b) rút gọn a
c) tìm x thuộc Z để A thuộc Z
Tìm đkxd của biểu thức Căn bậc hai x-2 +căn bậc hai6-2x Căn bậc hai x +2
a: ĐKXĐ: x-2>=0 và 6-2x>=0
=>2<=x<=3
b: DKXĐ: x+2>=0
=>x>=-2
Đúng 0
Bình luận (0)
\(\dfrac{x-2}{x+3}+\dfrac{x+5}{x+3}\)
a, Cộng hai phân thức
b, Tìm ĐKXD
a)\(=\dfrac{x-2+x+5}{x+3}=\dfrac{2x+3}{x+3}\)
b)ĐKXĐ: \(x+3\ne0\Leftrightarrow x\ne-3\)
Đúng 1
Bình luận (0)
a) Ta có: \(\dfrac{x-2}{x+3}+\dfrac{x+5}{x+3}\)
\(=\dfrac{x-2+\left(x+5\right)}{x+3}\)
\(=\dfrac{x-2+x+5}{x+3}\)
\(=\dfrac{2x+3}{x+3}\)
b) ĐKXĐ: \(x+3\ne0\)
hay \(x\ne-3\)
Đúng 0
Bình luận (0)
tìm ĐKXD( giải chi tiết nha)
\(\frac{5}{\sqrt{x-1}-2}\)
bt xác định \(\Leftrightarrow\sqrt{x-1}-2\ne0\)
\(\Leftrightarrow\sqrt{x-1}\ne2\)
\(\Leftrightarrow x-1\ne4\Leftrightarrow x\ne5\)
Đúng 0
Bình luận (0)
Bạn Đào Trọng Luân thiếu ĐK căn lớn hơn bằng 0
\(ĐKXĐ\hept{\begin{cases}x-1\ge0\\\sqrt{x-1}\ne2\end{cases}\Leftrightarrow}\hept{\begin{cases}x\ge1\\x-1\ne4\end{cases}\Leftrightarrow\hept{\begin{cases}x\ge1\\x\ne5\end{cases}}}\)
Đúng 0
Bình luận (0)
nếu mẫu là x2 + x + 1 thì đkxd của nó là j
-Không có ĐKXĐ, tức là với mọi x∈R thì phân thức luôn được xác định.
Đúng 1
Bình luận (0)
giúp vs mk cần gấp lắm r
A=x+2/x+3 - 5/x2+x-6 + 1/2-x
a) tìm đkxd của A c) tìm x để A= -3/4
b) rút gọn A d) tìm x thuộc z để a thuộc z
e)tính giá trị cảu A khi x2-9=0
a: ĐKXĐ: \(x\notin\left\{-3;2\right\}\)
b: \(A=\dfrac{x^2-4-5+x+3}{\left(x-2\right)\left(x+3\right)}=\dfrac{x^2+x-6}{\left(x-2\right)\left(x+3\right)}=\dfrac{x+2}{x-2}\)
c: Để A=3/4 thì 4x-8=3x+6
=>x=14
d: Để A nguyên thì \(x-2\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(x\in\left\{3;1;4;0;6;-2\right\}\)
Đúng 1
Bình luận (0)
cho P= \(\dfrac{2\sqrt{x}-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}+\dfrac{2\sqrt{x}+1}{\sqrt{x}-3}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\)
a, tìm đkxd của P
b, rút gọn P
c, tìm x để p=\(\dfrac{1}{2}\)
a: ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\notin\left\{9;4\right\}\end{matrix}\right.\)
b: Ta có: \(P=\dfrac{2\sqrt{x}-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}+\dfrac{2\sqrt{x}+1}{\sqrt{x}-3}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\)
\(=\dfrac{2\sqrt{x}-9+2x-3\sqrt{x}-2-x+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
Đúng 2
Bình luận (0)
cho biểu thức A =\(\frac{x}{x+2}\)+\(\frac{x+1}{x}\)
a)tìm ĐKXD
b)tìm giá trị của x để =2






















