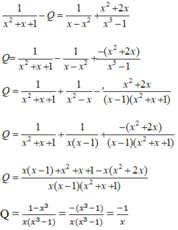Tìm x thuộc Z thỏa mái điều kiện sau : ( x2 - 5 ) ( x2 - 36 ) nhỏ hơn 0

Những câu hỏi liên quan
1) Cho phương trình x^2-2mx+2m-1=0. Định m để phương trình có hai nghiệm x1,x2 thỏa điều kiện: (x1+x2)^2 -x1x2 lớn hơn bằng 1
2) Phương trình x^2-mx+m-1=0 có hai nghiệm phân biệt x1, x2 thỏa điều kiện x1^2+x2^2 -(x1+x2) bé hơn bằng 12 khi m thuộc bao nhiêu?
Tìm giá trị của k để phương trình :x^2-(5+k)x+k=0 có hai nghiệm x1,x2 thỏa ̉mãn điều kiện x1^2+x2^2=18
Cho a,b,x,y là các số phức thỏa mãn các điều kiện
a
2
-
4
b
16
+
12
i
,
x
2
+
a
x
+
b
+
z
0
,
y
2
+
a
y
+
b
+
z
0
,
x...
Đọc tiếp
Cho a,b,x,y là các số phức thỏa mãn các điều kiện a 2 - 4 b = 16 + 12 i , x 2 + a x + b + z = 0 , y 2 + a y + b + z = 0 , x - y = 2 3 . Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của z . Tính M+m.
![]()
![]()
![]()
![]()
Cho phương trình x 2 - 3x + m - 5 = 0. Tìm m để phương trình có 2 nghiệm phân biệt x 1 ; x 2 thỏa mãn điều kiện x 1 ; x 2 =4
x 2 - 3x + m - 5 = 0
a = 1; b = -3; c = m – 5
Δ = b 2 - 4ac = - 3 2 - 4(m - 5) = 29 - 4m
Phương trình có 2 nghiệm phân biệt x 1 ; x 2 khi và chỉ khi
Δ > 0 ⇔ 29 - 4m > 0 ⇔ m < 29/4
Theo định lí Vi-et ta có:
x 1 ; x 2 = c/a = m - 5
Theo bài ra
x 1 ; x 2 = 4 ⇔ m - 5 = 4 ⇔ m = 9 (Không TMĐK m < 29/4)
Vậy không tồn tại m thỏa mãn đề bài.
Đúng 0
Bình luận (0)
Cho phương trình: x^2 + (4m+1)x +2(m-4)=0
a) Tìm m để pt có 2 nghiệm thỏa mãn điều kiện x2-x1=17
b) Tìm m để A=(x1-x2)^2 có giá trị nhỏ nhất
c) Tìm hệ thức liên hệ giữa 2 nghiệm ko phụ thuộc m
Mk cần gấp lm, mấy bn giải dùm mk nha
Cho phương trình x²-2x+m-3=0 a) tìm điều kiện của m để phương trình có nghiệm số b)tìm m để phương trình trên có 2 nghiệm x1;x2 thỏa điều kiện x1-x2=4
a: Để phương trình có nghiệm thì (-2)^2-4(m-3)>=0
=>4-4m+12>=0
=>-4m+16>=0
=>-4m>=-16
=>m<=4
b: x1-x2=4
x1+x2=2
=>x1=3; x2=-1
x1*x2=m-3
=>m-3=-3
=>m=0(nhận)
Đúng 0
Bình luận (0)
cho ba số thực dương x,y,z thỏa mãn điều kiện x2≥y+z .Tìm giá trị nhỏ nhất của biểu thức : P = \(\dfrac{1}{x^2}\left(y^2+z^2\right)+\dfrac{7x^2}{2}\left(\dfrac{1}{y^2}+\dfrac{1}{z^2}\right)+2007\)
Lời giải:
Sửa: $x^2\geq y^2+z^2$
Áp dụng BĐT Cauchy-Schwarz:
$P\geq \frac{y^2+z^2}{x^2}+\frac{7x^2}{2}.\frac{4}{y^2+z^2}+2007$
$=\frac{y^2+z^2}{x^2}+\frac{14x^2}{y^2+z^2}+2007$
$=\frac{y^2+z^2}{x^2}+\frac{x^2}{y^2+z^2}+\frac{13x^2}{y^2+z^2}+2007$
$\geq 2+\frac{13x^2}{y^2+z^2}+2007$ (áp dụng BĐT Cô-si)
$\geq 2+13+2007=2022$ (do $x^2\geq y^2+z^2$)
Vậy $P_{\min}=2022$
Đúng 1
Bình luận (0)
tìm x,biết : x2-3x-4=0
tìm giá trị của ẩn số thỏa điều kiện cho sẵn
\(x^2\) - 3\(x\) - 4 = 0
(\(x^2\) + \(x\)) - (4\(x\) + 4) = 0
\(x\).(\(x\) + 1) - 4.(\(x\) + 1) = 0
(\(x\) + 1).(\(x\) - 4) = 0
\(\left[{}\begin{matrix}x+1=0\\x-4=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-1\\x=4\end{matrix}\right.\)
Vậy \(x\in\) {-1; 4}
Đúng 0
Bình luận (0)
Trong mỗi trường hợp sau hãy tìm phân thức Q thỏa mãn điều kiện :
1
x
2
+
x
+
1
-
Q
1
x
-
x
2
+
x
2
+...
Đọc tiếp
Trong mỗi trường hợp sau hãy tìm phân thức Q thỏa mãn điều kiện : 1 x 2 + x + 1 - Q = 1 x - x 2 + x 2 + 2 x x 3 + 1