Dựa vào định lí Py-ta-go
Chứng minh:[a+b].[a-b] = a*2-b*2
Gọi a,b,c là các cạnh của 1 tam giác vuông.Gọi h là đường cao ứng với cạnh huyền a..Chứng minh : Tam giác có các cạnh a+h;b+c và h cũng là 1 tam giác vuông. ( Dùng định lí Py-ta-go đảo để giải, thầy mình gợi ý vậy )
Câu này dễ mak
Ta có tam giác vuông có 3 cạnh b,c,a với h là đường cao ứng với cạnh huyền a, ta có
+) b^2 + c^2 = a^2 (Định lí Pi-ta-go)
+) ah = bc(Hệ thức lượng)
Ta có:
+) (b + c)^2 + h^2 = b^2 + 2bc + c^2 + h^2 = a^2 + 2ah + h^2
+) (a + h)^2 = a^2 + 2ah + h^2
Từ đây suy ra: (b + c)^2 + h^2 = (a + h)^2
=> Tam giác có 3 cạnh là b + c; a+ h và h là tam giác vuông (Định lí Py-ta-go đảo)
Hãy chứng minh định lí py-ta-go và py-ta-go đảo
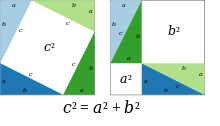
Định lý Pytago đã được biết đến từ lâu trước thời của Pythagoras, nhưng ông được coi là người đầu tiên nêu ra chứng minh định lý này.[2] Cách chứng minh của ông rất đơn giản, chỉ bằng cách sắp xếp lại hình vẽ.
Trong hai hình vuông lớn ở hình minh họa bên trái, mỗi hình vuông chứa bốn tam giác vuông bằng nhau, sự khác nhau giữa hai hình vuông này là các tam giác vuông được bố trí khác nhau. Do vậy, khoảng trắng bên trong mỗi hình vuông phải có diện tích bằng nhau. Dựa vào hình vẽ, hai vùng trắng có diện tích bằng nhau cho phép rút ra được kết luận của định lý Pytago, Q.E.D.[9]
Về sau, trong tác phẩm của nhà triết học và toán học Hy Lạp Proclus đã dẫn lại chứng minh rất đơn giản của Pythagoras.[10] Các đoạn dưới đây nêu ra một vài cách chứng minh khác, nhưng cách chứng minh ở trên thuộc về của Pythagoras
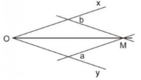
Hình 31 cho biết cách vẽ tia phân giác của góc xOy bằng thước hai lề:
Áp một lề của thước vào cạnh Ox, kẻ đường thẳng a theo lề kia.
Làm tương tự với cạnh Oy, ta kẻ được đường thẳng b.
Gọi M là giao điểm của a và b, ta có OM là tia phân giác của góc xOy.
Hãy chứng minh tia OM được vẽ như vậy đúng là tia phân giác của góc xOy.
(Gợi ý: Dựa vào bài tập 12 chứng minh các khoảng cách từ M đến Ox và đến Oy bằng nhau (do cùng bằng khoảng cách hai lề của chiếc thước) rồi áp dụng định lí 2)
Hình 31
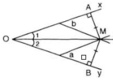
(Từ bài tập 12 ta biết rằng: độ dài đường vuông góc giữa hai đường thẳng song song chính là khoảng cách giữa hai đường thẳng đó.)
Gọi A, B lần lượt là chân đường cao hạ từ M xuống Ox, Oy ⇒ MA, MB lần lượt là khoảng cách từ M đến Ox, Oy.
Theo cách vẽ bằng thước hai lề và từ bài tập 12 ta suy ra: MA = MB (cùng bằng khoảng cách hai lề của thước) hay điểm M cách đều hai cạnh của góc xOy.
Áp dụng định lý 2 suy ra: OM là tia phân giác của góc xOy.
Cho tam giác ABC có góc A = 90 độ, BC = 10 cm , AC = căn hai của 75
a, Tính AB
b, Tính góc C và góc B
( Cái này là về định lí Py-ta-go nha các bạn)
Xét tam giác ABC có A=90 độ=>tam giác ABC vuông ở A
áp dụng Py-ta-go :
BC2=AB2+AC2
=>102=AB2+(căn 75)2
=>100=AB2+75
=>AB2=25=>AB=5(cm)
câu b tự lm nhé bn,dễ lắm
Xét tam giác ABC có A=90 độ
=>tam giác ABC vuông ở A ( theo định lí Pytago đảo)
Theo định lí Py-ta-go ta có:
BC2=AB2+AC2
=>102=AB2+(\(\sqrt{75}\))2
=>100=AB2+75
=>AB2=25
=>AB=5(cm)
b)Ta có: AB=5cm (chứng minh trên)
BC=10cm (GT)
=>AB= 1/2 BC
=>Tam giác ABC là tam giác nửa đều
=> góc B=60o và góc C=30o (tính chất tam giác nửa đều)
Xét tam giác ABC có A=90 độ
=>tam giác ABC vuông ở A ( theo định lí Pytago đảo)
Theo định lí Py-ta-go ta có:
BC2=AB2+AC2
=>102=AB2+(√75)2
=>100=AB2+75
=>AB2=25
=>AB=5(cm)
b)Ta có: AB=5cm (chứng minh trên)
BC=10cm (GT)
=>AB= 1/2 BC
=>Tam giác ABC là tam giác nửa đều
=> góc B=60o và góc C=30o (tính chất tam giác nửa đều)
1.Cho tam giác ABC vuông tại A có đường cao AH . C/M:
a,AB^2=BC.BH ; AC^2=BC.CH . Từ dố chứng minh định lý py-ta -go
b,AH^2=BH.CH
c,1/AH^2=1/AB^2+1/AC^2
d,AH.BC=AB.AC
Lời giải:
1.
Xét tam giác $BHA$ và $BAC$ có:
$\widehat{B}$ chung
$\widehat{BHA}=\widehat{BAC}=90^0$
$\Rightarrow \triangle BHA\sim \triangle BAC$ (g.g)
$\Rightarrow \frac{BH}{BA}=\frac{BA}{BC}\Rightarrow BA^2=BH.BC$
Tương tự, ta cũng cm được: $\triangle CHA\sim \triangle CAB$ (g.g)
$\Rightarrow CA^2=CH.CB$
Do đó:
$CA^2+CB^2=BH.BC+CH.CB=BC(BH+CH)=BC.BC=BC^2$
(đpcm)
b. Xét tam giác $BHA$ và $AHC$ có:
$\widehat{BHA}=\widehat{AHC}=90^0$
$\widehat{HBA}=\widehat{HAC}$ (cùng phụ $\widehat{BAH}$)
$\Rightarrow \triangle BHA\sim \triangle AHC$ (g.g)
$\Rightarrow \frac{BH}{AH}=\frac{HA}{HC}$
$\Rightarrow AH^2=BH.CH$
c.
$\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{AB^2+AC^2}{AB^2.AC^2}$
$=\frac{BC^2}{AB^2.AC^2}=(\frac{BC}{AB.AC})^2=(\frac{BC}{2S_{ABC}})^2$
$=(\frac{BC}{AH.BC})^2=\frac{1}{AH^2}$
.d. Hiển nhiên theo công thức diện tích.
Dựa vào Atlat địa lí Việt nam và kiến thức đã học. Hãy :
a) Xác định vùng sản xuất lúa lớn nhất nước ta
b) Trình bày nguyên nhân dẫn đến sự hình thành các vùng trọng điểm lúa của cả nước.
a) Vùng sản xuất lúa lớn nhất ở nước ta là vùng Đồng bằng Sông Cửu Long
b) Nguyên nhân dẫn đến hình thành các vùng trọng điểm lúa
- Điều kiện tự nhiên :
+ Đất phù sa màu mỡ, diện tích rộng, địa hình bằng phẳng
+ Khí hậu nhiệt đới ẩm gió mùa
+ Sông ngòi dày đặc, nguồn nước phong phú
- Điều kiện kinh tế - xã hội
+ Nguồn lao động dồi dào, giàu kinh nghiệm trong sản xuất lúa
+ Nhà nước quan tâm đầu tư phát triển, cơ sở vật chất - kĩ thuật không ngừng được tăng trưởng
+ Thị trường tiêu thụ ngày càng mở rộng
Chứng minh định lí Py ta go,
ai là người phát minh ra định lí py-ta go
Định lý này được đặt tên theo nhà vật lí học và nhà toán học Hy Lạp Pytago
Sử dụng tích vô hướng, chứng minh định lí Pythagore: Tam giác ABC vuông tại A khi và chỉ khi \(B{C^2} = A{B^2} + A{C^2}\).
Áp dụng định lí cosin trong tam giác ABC, ta có:
\(B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\)
Ta có: \(\widehat A = {90^o}\) (tam giác ABC vuông tại A) \( \Leftrightarrow \cos A = \cos {90^o} = 0\)
\( \Leftrightarrow B{C^2} = A{B^2} + A{C^2}\) (đpcm)