tìm x, y
3xy - x + 3y - 1 = 15
Bài 1 : Tìm x và y , biết : 3xy - x + 3y - 1 = 15
ta có: 3xy-x+3y-1=15<=>(3xy-x)+(3y-1)=15<=>x(3y-1)+(3y-1)=15<=>(x+1)(3y-1)=15=> x+1 và 3y-1 thuộc Ư(15) từ đó tính đó tính tiếp
3xy-x+3y-1=15
=>3y(x+1)-(x+1)=15
=>(3y-1)(x+1)=15
ta co 15=1x15=(-1)x(-15)=3x5=-3x(-5) và ngược lại
rồi câu thử từng trường hợp nhé
Tìm các số nguyên x,y thoả mãn: 3xy+x-3y\(3xy+x-3y=5\)
\(3xy+x-3y=5\\ \Rightarrow x\left(3y+1\right)-3y-1=5-1\\ \Rightarrow x\left(3y+1\right)-\left(3y-1\right)=4\\ \Rightarrow\left(x-1\right)\left(3y-1\right)=4\)
Vì \(x,y\in Z\Rightarrow\left\{{}\begin{matrix}x-1,3y-1\in Z\\x-1,3y-1\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\end{matrix}\right.\)
Ta có bảng:
| x-1 | 1 | 2 | 4 | -1 | -2 | -4 |
| 3y-1 | 4 | 2 | 1 | -4 | -2 | -1 |
| x | 2 | 3 | 5 | 0 | -1 | -3 |
| y | \(\dfrac{5}{3}\left(loại\right)\) | 1 | \(\dfrac{2}{3}\left(loại\right)\) | -1 | \(-\dfrac{1}{3}\left(loại\right)\) | 0 |
Vậy \(\left(x,y\right)\in\left\{\left(3;1\right);\left(0;-1\right);\left(-3;0\right)\right\}\)
tìm x,y :
a) xy+x+y=2
b)2x^2+4x=15-3y^2
c)2x^2+3xy-2y^2=7
a,(2x+3)^3 b,(x-3y)^3 c.(x+4)(x^2-4x+15) d,(1/3x+1y)(1/9x^2-2/3xy+4y) e,(x-3y)(x^2+3xy+9y^2)
a: \(\left(2x+3\right)^3=8x^3+36x^2+54x+27\)
b: \(\left(x-3y\right)^3=x^3-9x^2y+27xy^2-27y^3\)
Thu gọn đa thức, tìm bậc và tính giá trị đa thức tại x = −1; y =1:
A=4\(X^3Y-XY-\dfrac{9}{2}X^3Y+3XY-1\)
Thay x=-1, y=1 vào A ta có:
\(A=4x^3y-xy-\dfrac{9}{2}x^3y+3xy-1\\
=-\dfrac{1}{2}x^3y+2xy-1\\
=-\dfrac{1}{2}.\left(-1\right)^3.1+2.\left(-1\right).1-1\\
=\dfrac{1}{2}-2-1\\
=
-\dfrac{5}{2}\)
Xét các số thực dương x, y thỏa mãn log 3 1 - y x + 3 x y = 3 x y + x + 3 y - 4 . Tìm giá trị nhỏ nhất P m i n của P = x + y
A. P m i n = 4 3 + 4 3
B. P m i n = 4 3 - 4 3
C. P m i n = 4 3 - 4 9
D. P m i n = 4 3 + 4 9
Xét các số thực dương x, y thỏa mãn log 3 1 - y x + 3 x y = 3 x y + x + 3 y - 4 . Tìm giá trị nhỏ nhất P m i n của P = x + y
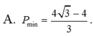
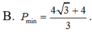
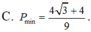
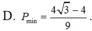
Bài 1 : tìm x,y thuộc Z, biết
a) ( x - 1 ) . ( y + 3) = 5
b) x . 3xy + 3y = 12
Tìm các số nguyên x, y biết:
2x2 + 3xy + y2 - 4x - 3y + 1 = 0