tìm Min:
B=x mux2 - 2xy +4y(y mũ 2) -10y -2x +18
Tìm max : a) \(M=-2x^2+3x+1\)
b) \(N=-x^2+2xy-4y^2+2x+10y+5\)
a: \(M=-2\left(x^2-\dfrac{3}{2}x-\dfrac{1}{2}\right)\)
\(=-2\left(x^2-2\cdot x\cdot\dfrac{3}{4}+\dfrac{9}{16}-\dfrac{17}{16}\right)\)
\(=-2\left(x-\dfrac{3}{4}\right)^2+\dfrac{17}{8}\le\dfrac{17}{8}\forall x\)
Dấu '=' xảy ra khi x=3/4
b: Tham khảo:
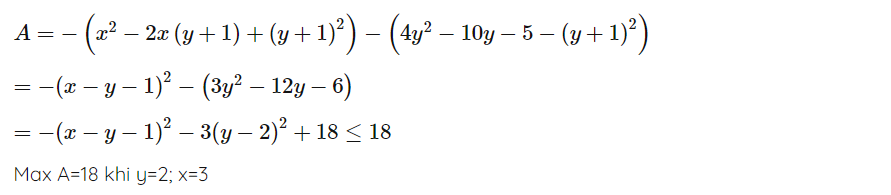
Tìm \(x,\) \(y\) sao cho:
\(B=-x^2+2xy-4y^2+2x+10y-8\) có \(GTLN\)
Tìm gtln và gtnn a) M=10x2 + 6y + 4y2 + 4xy + 2 b) H= -x2 + 2xy - 4y2 + 2x + 10y - 8 c) K= 2x2 + 2xy - 2x + 2xy + y2
a) \(M=10x^2+6y+4y^2+4xy+2\)
\(=\left(10x^2+4xy+\dfrac{2}{5}y^2\right)+\left(\dfrac{18}{5}y^2+6y+\dfrac{5}{2}\right)-\dfrac{1}{2}\)
\(=10\left(x^2+\dfrac{2}{5}xy+\dfrac{1}{25}y^2\right)+\dfrac{18}{5}\left(y^2+\dfrac{5}{3}y+\dfrac{25}{36}\right)-\dfrac{1}{2}\)
\(=10\left(x+\dfrac{1}{5}y\right)^2+\dfrac{18}{5}\left(y+\dfrac{5}{6}\right)^2-\dfrac{1}{2}\ge-\dfrac{1}{2}\)
Đẳng thức xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x+\dfrac{1}{5}y=0\\y+\dfrac{5}{6}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{6}\\y=-\dfrac{5}{6}\end{matrix}\right.\)
b) \(H=-x^2+2xy-4y^2+2x+10y-8\)
\(=-x^2+2x\left(y+1\right)-\left(y^2+2y+1\right)-\left(3y^2-12y+7\right)\)
\(=-x^2+2x\left(y+1\right)-\left(y+1\right)^2-3\left(y^2-4y+4\right)+5\)
\(=-\left(x-y-1\right)^2-3\left(y-2\right)^2+5\le5\)
Đẳng thức xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x-y-1=0\\y-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=2\end{matrix}\right.\)
c) \(K=2x^2+2xy-2x+2xy+y^2\)
bn xem lại cái đề nhé, sao lại có 2 lần 2xy
1) Thực hiện phép tính :
a) -(5x - 4)(2x+3)
b) ( x - y)( x mũ 2 + xy+ y mũ 2)
c) 7x( x - 4) - ( 7x +3)(2x mũ 2 - x+4)
2) Chứng minh rằng giá trị của biểu thức không phụ thuộc vào giá trị của biến x:
a) x(3x +12) - ( 7x - 20) + x(2x - 3) - x( 2x +5)
b) 3( 2x-1) - 5( x-3) + 6( 3x - 4) - 19x
3) tìm x:
a) 3x( x - 2) - x( 1+3x) = 14
b) (2x - 1)( x + 5) - (2x +1)( x + 4,5)=3,5
c) 3x mũ 2 - 3x( x - 3) = 36
d) (3x + 1)(x - 1) + x( 4 - 3x )= 5
4/ Phân tích đa thức thành nhân tử:
a. 14xy - 21xy - 28xy
b. x( x + y) - 5x - 5y
c. 10x( x - y ) - 8( y - x )
d. x mũ 3 - x + 3x mũ 2 y + 3 xy mũ 2 + y mũ 3 - y
e. x mũ 2 + 7x - 8
f. 2x mũ 2 - 3x - 2
g. - 5x mũ 2 + 16x - 3
h. x mũ 2 - 2xy - 3y mũ 2
i. x mũ 2 - 2xy + y mũ 2 - z mũ 2
Giải hộ mình với ạ ....
Bài 4:
a: \(=7xy\left(2-3-4\right)=-35xy\)
b: \(=\left(x-5\right)\left(x+y\right)\)
c: \(=10x\left(x-y\right)+8\left(x-y\right)=2\left(x-y\right)\left(5x+4\right)\)
d: \(=\left(x+y\right)^3-\left(x+y\right)\)
=(x+y)(x+y+1)(x+y-1)
e: =x^2+8x-x-8
=(x+8)(x-1)
f: \(=2x^2-4x+x-2=\left(x-2\right)\left(2x+1\right)\)
g: =-5x^2+15x+x-3
=(x-3)(-5x+1)
h: =x^2-3xy+xy-3y^2
=x(x-3y)+y(x-3y)
=(x-3y)*(x+y)
1) Thực hiện phép tính :
a) -(5x - 4)(2x+3)
b) ( x - y)( x mũ 2 + xy+ y mũ 2)
c) 7x( x - 4) - ( 7x +3)(2x mũ 2 - x+4)
2) Chứng minh rằng giá trị của biểu thức không phụ thuộc vào giá trị của biến x:
a) x(3x +12) - ( 7x - 20) + x(2x - 3) - x( 2x +5)
b) 3( 2x-1) - 5( x-3) + 6( 3x - 4) - 19x
3) tìm x:
a) 3x( x - 2) - x( 1+3x) = 14
b) (2x - 1)( x + 5) - (2x +1)( x + 4,5)=3,5
c) 3x mũ 2 - 3x( x - 3) = 36
d) (3x + 1)(x - 1) + x( 4 - 3x )= 5
4/ Phân tích đa thức thành nhân tử:
a. 14xy - 21xy - 28xy
b. x( x + y) - 5x - 5y
c. 10x( x - y ) - 8( y - x )
d. x mũ 3 - x + 3x mũ 2 y + 3 xy mũ 2 + y mũ 3 - y
e. x mũ 2 + 7x - 8
f. 2x mũ 2 - 3x - 2
g. - 5x mũ 2 + 16x - 3
h. x mũ 2 - 2xy - 3y mũ 2
i. x mũ 2 - 2xy + y mũ 2 - z mũ 2
Giải hộ mình với ạ ....
Bài 4:
a: \(=7xy\left(2-3-4\right)=-35xy\)
b: \(=\left(x-5\right)\left(x+y\right)\)
c: \(=10x\left(x-y\right)+8\left(x-y\right)=2\left(x-y\right)\left(5x+4\right)\)
d: \(=\left(x+y\right)^3-\left(x+y\right)\)
=(x+y)(x+y+1)(x+y-1)
e: =x^2+8x-x-8
=(x+8)(x-1)
f: \(=2x^2-4x+x-2=\left(x-2\right)\left(2x+1\right)\)
g: =-5x^2+15x+x-3
=(x-3)(-5x+1)
h: =x^2-3xy+xy-3y^2
=x(x-3y)+y(x-3y)
=(x-3y)*(x+y)
tìm gtnn
d. D(x) = 2x² + 3y² + 4xy-8x-2y + 18 e. E(x) = 2x² + 3y² + 4z²-2(x+y+z) + 2 f F(x)=2x² +8xy + 11y2-4x-2y+6 g. G(x)=2x²+2y+z²+2xy-2xz-2yz-2x-4y h. H(x)=x² + y²-xy-x+y+1 Bài 2: Tim GTLN của các biểu thức sau a. A=4x²-5y² +8xy+10y+12
b.B=-x²-y²+xy+2x+2y
tìm gtnn
d. D(x) = 2x² + 3y² + 4xy-8x-2y + 18 e. E(x) = 2x² + 3y² + 4z²-2(x+y+z) + 2 f F(x)=2x² +8xy + 11y2-4x-2y+6 g. G(x)=2x²+2y+z²+2xy-2xz-2yz-2x-4y h. H(x)=x² + y²-xy-x+y+1 Bài 2: Tim GTLN của các biểu thức sau a. A=4x²-5y² +8xy+10y+12
b.B=-x²-y²+xy+2x+2y
tìm gtnn
d. D(x) = 2x² + 3y² + 4xy-8x-2y + 18 e. E(x) = 2x² + 3y² + 4z²-2(x+y+z) + 2 f F(x)=2x² +8xy + 11y2-4x-2y+6 g. G(x)=2x²+2y+z²+2xy-2xz-2yz-2x-4y h. H(x)=x² + y²-xy-x+y+1 Bài 2: Tim GTLN của các biểu thức sau a. A=4x²-5y² +8xy+10y+12
b.B=-x²-y²+xy+2x+2y
Ta có:
D=2x2+3y2+4xy−8x−2y+18C=2x2+3y2+4xy−8x−2y+18
D=2(x2+2xy+y2)+y2−8x−2y+18C=2(x2+2xy+y2)+y2−8x−2y+18
D=2[(x+y)2−4(x+y)+4]+(y2+6y+9)+1C=2[(x+y)2−4(x+y)+4]+(y2+6y+9)+1
D=2(x+y−2)2+(y+3)2+1≥1C=2(x+y−2)2+(y+3)2+1≥1
Dấu "=" xảy ra ⇔x+y=2⇔x+y=2và y=−3y=−3
Hay x = 5 , y = -3
Đc chx bạn
Tìm x, y sao cho: B=-x^2+2xy-4y^2+2x+10y-8 có giá trị lớn nhất
B=-x^2+2xy-4y^2+2x+10y-8
B = (-x^2 - y^2 - 1 + 2xy + 2x - 2y) + (-3y^2 + 12y - 12) + 5
B = -(x^2+y^2+1 - 2xy - 2x + 2y) - 3(y^2 - 4y + 4) + 5
B = - (x - y - 1)^2 - 3(y - 2)^2 +5 5
Max B = 5 khi x = 3, y = 2
B=-x^2+2xy-4y^2+2x+10y-8
B= x^2-2xy+4y^2-2x-10y+8
B= ( x^2+y^2+1-2xy-2x+2y) +(3y^2-12y+7)
B=(x-y-1)^2+ 3(y^2-4y+7/4)=(x-y-1)^2+3(y-2)^2-27/4>=-... nen A<= 27/4
ban tu tim dau = nhe
nhok lạnh lùng sai oy (3y2-12y+7) =3(y^2-4y+7/3) ri nè