a: \(M=-2\left(x^2-\dfrac{3}{2}x-\dfrac{1}{2}\right)\)
\(=-2\left(x^2-2\cdot x\cdot\dfrac{3}{4}+\dfrac{9}{16}-\dfrac{17}{16}\right)\)
\(=-2\left(x-\dfrac{3}{4}\right)^2+\dfrac{17}{8}\le\dfrac{17}{8}\forall x\)
Dấu '=' xảy ra khi x=3/4
b: Tham khảo:
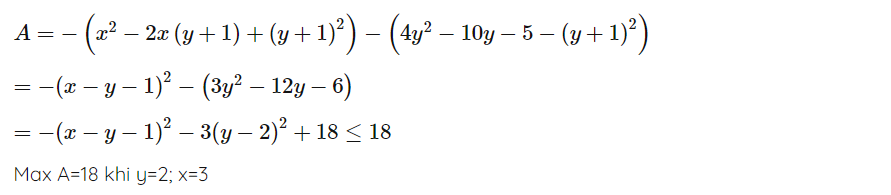
a: \(M=-2\left(x^2-\dfrac{3}{2}x-\dfrac{1}{2}\right)\)
\(=-2\left(x^2-2\cdot x\cdot\dfrac{3}{4}+\dfrac{9}{16}-\dfrac{17}{16}\right)\)
\(=-2\left(x-\dfrac{3}{4}\right)^2+\dfrac{17}{8}\le\dfrac{17}{8}\forall x\)
Dấu '=' xảy ra khi x=3/4
b: Tham khảo:
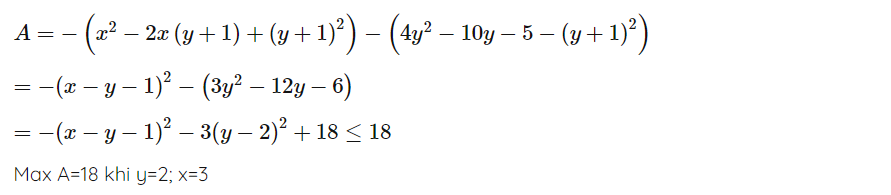
Tìm max : \(-x^2+2xy-4y^2+2x+10y+5\)
Tìm Max:
a) A=-x2 +2xy -4y2 +2x + 10y +5
b) B=-x2 -2y2 -2xy +2x -2y -15
Tìm min : a) \(M=x^2-2xy+2y^2-4y+2016\)
b) \(N=x^2-2xy+2x+2y^2-4y+2016\)
Bài 1: Rút gọn biểu thức sau:
A/ (x+3).(x^2-3x+9) -(54+x^3)
B/ (2x+y).(4x^2-2xy+y^2)-(2x-y).(4x^2+2xy+y^2)
C/ (2x-1)^2- (2x+2)^2
D/ (a+b)^3 - 3ab.(a+b)
Bài 2: tìm x, biết
A/ x^2-2x +1=25
B/ x^3 -3x^2= -3x+1
Bài 3 chứng minh rằng giá trị của biểu thức sau luôn dương với mọi giá trị của biến
A/ A= 4x^2+4x+2
B/ B= 2x^2-2x+1
tìm x,y sao cho :
a. \(A=2x^2+9y^2-6xy-6x-12y+2014\) đạt giá trị nhỏ nhất ?
b. \(B=-x^2+2xy-4y^2+2x+10y-8\) đạt giá trị lớn nhất ?
bai1: rut gon cac bieu thuc sau
a, (2x-y).(4x^2+2xy+y^2)-(2x+y).(4x^2-2xy+y^2)
b, (3x+2y).(9x^2-6xy+4y^2)-27x^3
c,8x.(x-2y).(x+2y)+(y-2x).(x^2+2xy+4x^2)
bai2 :cmr
a, a^3+b^3=(a+b)^3-3ab.(a+b)
b.a^3-b^3=(a-b)+3ab,(a-b)
Tìm \(x,y\in Z\) thỏa : a) \(x^2-2x+4y^2+8y+5=0\)
b) \(x^2-2xy+2y^2-2x+6y+5=0\)
a) Tìm min \(M=2x^2+9y^2-16x-12y+2017\)
b) Tìm max : \(N=-x^2-4y^2+6y+2x-2016\)
Tìm x ; y sao cho
A = 2x2 + 9y2 - 6xy - 6x - 12xy + 2010 đạt giá trị nhỏ nhất
B = -x2 + 2xy - 4y + 2x + 10y - 8 đạt giá trị lớn nhất