Ta có:

\(\widehat{A}=\widehat{C}=50^o\)

\(\widehat{B}=\widehat{C}=130^o\)

nhanh lên

Câu 10:

góc A=180-130=50 độ

góc B=(180+50)/2=230/2=115 độ

góc C=180-115=65 độ

có ai biết làm bài 11 ko a

a) Ta thấy : BAD = BCD = 120°( tính chất) 

Mà AB//CD ( ABCD là hình bình hành) 

=> ABC + BCD = 180° 

=> ABC = ADC = 60°

Trong tính chất của hình bình hành:

Định lí: Trong hình bình hành:

+ Các cạnh đối bằng nhau.

+ Các góc đối bằng nhau.

+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường

Vì ABCD là hbh nên \(\widehat{A}=\widehat{C}=120^0\) và AB//CD

Do đó \(\widehat{B}=\widehat{D}=180^0-\widehat{A}=60^0\) (trong cùng phía)

\(\widehat{A}=\widehat{C}=135^0\)

\(\widehat{B}=\widehat{D}=45^0\)

Bài 1:

ABCD là hình bình hành

=>AD=BC(1)

E là trung điểm của AD

=>\(EA=ED=\dfrac{AD}{2}\left(2\right)\)

F là trung điểm của BC

=>\(FB=FC=\dfrac{BC}{2}\left(3\right)\)

Từ (1),(2),(3) suy ra EA=ED=FB=FC

Bài 2:

a: ABCD là hình bình hành

=>\(\widehat{A}+\widehat{B}=180^0\)

=>\(\widehat{B}=180^0-60^0=120^0\)

ABCD là hình bình hành

=>\(\widehat{A}=\widehat{C};\widehat{B}=\widehat{D}\)

\(\widehat{A}=\widehat{C}\)

mà \(\widehat{A}=60^0\)

nên \(\widehat{C}=60^0\)

\(\widehat{B}=\widehat{D}\)

mà \(\widehat{B}=120^0\)

nên \(\widehat{D}=120^0\)

b: ABCD là hình bình hành

=>\(\widehat{A}=\widehat{C}\)

mà \(\widehat{A}+\widehat{C}=140^0\)

nên \(\widehat{A}=\widehat{C}=\dfrac{140^0}{2}=70^0\)

ABCD là hình bình hành

=>\(\widehat{A}+\widehat{B}=180^0\)

=>\(\widehat{B}=180^0-70^0=110^0\)

ABCD là hình bình hành

=>\(\widehat{B}=\widehat{D}\)

mà \(\widehat{B}=110^0\)

nên \(\widehat{D}=110^0\)

c: ABCD là hình bình hành

=>\(\widehat{B}+\widehat{A}=180^0\)

mà \(\widehat{B}-\widehat{A}=40^0\)

nên \(\widehat{B}=\dfrac{180^0+40^0}{2}=110^0;\widehat{A}=\dfrac{180^0-40^0}{2}=70^0\)

ABCD là hình bình hành

=>\(\widehat{A}=\widehat{C};\widehat{B}=\widehat{D}\)

=>\(\widehat{C}=70^0;\widehat{D}=110^0\)

mình dốt hình lắm chỉ biết số học thôi

CHÚC BẠN HỌC GIỎI

TK MÌNH NHÉ

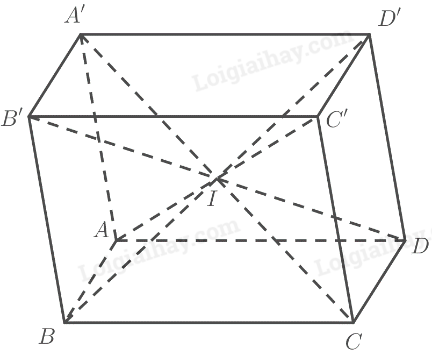
a) Vì \(ABCD.A'B'C'D'\) là hình lăng trụ nên có:

‒ Hai đáy \(ABCD\) và \(A'B'C'D'\) bằng nhau và là hình bình hành.

‒ Các mặt bên \(AA'B'B,AA'D'D,BB'C'C,CC'D'D\) là các hình bình hành.

b) Ta có:

\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( {AA'C'C} \right) \cap \left( {ABC{\rm{D}}} \right) = AC\\\left( {AA'C'C} \right) \cap \left( {A'B'C'D'} \right) = A'C'\end{array} \right\} \Rightarrow AC\parallel A'C'\)

Mà \(AA'\) và \(CC'\) là các cạnh bên của hình lăng trụ nên \(AA'\parallel CC'\)

Vậy \(AA'C'C\) là hình bình hành.

\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( {BB'D'D} \right) \cap \left( {ABC{\rm{D}}} \right) = B{\rm{D}}\\\left( {BB'D'D} \right) \cap \left( {A'B'C'D'} \right) = B'D'\end{array} \right\} \Rightarrow B{\rm{D}}\parallel B'D'\)

Mà \(BB'\) và \(DD'\) là các cạnh bên của hình lăng trụ nên \(BB'\parallel DD'\)

Vậy \(BB'D'D\) là hình bình hành.

c) Ta có:

\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( {A'B'C{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right) = C{\rm{D}}\\\left( {A'B'C{\rm{D}}} \right) \cap \left( {A'B'C'D'} \right) = A'B'\end{array} \right\} \Rightarrow C{\rm{D}}\parallel A'B'\left( 1 \right)\)

\(ABC{\rm{D}}\) là hình bình hành nên \(AB = CD\)

\(AA'B'B\) là hình bình hành nên \(AB = A'B'\)

Vậy \(A'B' = CD\left( 2 \right)\)

Từ (1) và (2) suy ra \(A'B'C{\rm{D}}\) là hình bình hành

\( \Rightarrow A'C,B'D\) cắt nhau tại trung điểm của mỗi đường.

Chứng minh tương tự ta có:

+ \(ABC'D'\) là hình bình hành nên \(AC',B{\rm{D}}'\) cắt nhau tại trung điểm của mỗi đường

+ \(A'BCD'\) là hình bình hành nên \(A'C,B{\rm{D}}'\) cắt nhau tại trung điểm của mỗi đường

Do đó bốn đoạn thẳng \(A'C,AC',B'D,BD\) có cùng trung điểm.