Nhờ mọi người giúp vs, em đg cần gấp ạ, cho em xin cả cách giải với ạ. Em cảm ơn mọ người



Những câu hỏi liên quan
Cần gấp ạ, xin mọi người giúp em vs ạ. Em cảm ơn mọi người. Nếu đc em xin cả cách giải ạ


Hướng dẫn: A đạt GTLN khi \(\dfrac{1}{A}\) đạt GTNN
Ta có: \(x^2+2\ge0\forall x\)
\(\Rightarrow A=\dfrac{1}{x^2+2}\le\dfrac{1}{2}\forall x\)
Vậy GTLN của A là 1/2
=> A
Đúng 2
Bình luận (1)
Câu 2: B đạt GTLN khi và chỉ khi x2 đạt giá trị nhỏ nhất
⇔ x2=0 ⇒B = 10 - 0= 0
Chọn đáp án B nhe
Câu 3: Có A= 4x - 2x2= (-2x2 + 4x - 1) + 1=\(-2\left(x^2-2x+1\right)+1\)
⇔ A= \(-2\left(x-1\right)^2+1\le1\)
Chọn đáp án B nha
Đúng 2
Bình luận (0)
Mọi người giúp em với ạ, nếu đc thù em xin cả cách giải, em đang cần gấp lắm ạ, cảm ơn mọi người nhiều


Câu 1: A
Câu 2: B
Câu 3: D
Câu 4: A
Câu 5: C
Câu 6: B
Câu 7: A
Câu 9: B
Đúng 1
Bình luận (0)
Xin mọi người giúp vs ạ, em đang cần gấp lắm ạ.Nếu đc cho em xin cả cách giải ạ


Câu 1: A
Câu 2: B
Câu 3: D
Câu 4: A
Câu 5: C
Câu 6: B
Đúng 1
Bình luận (0)
Cần mọi người giúp ạ, nếu đc thì cho em xin cả cách giải, em cảm ơn ạ (°v°)


Câu 1: A
Câu 2: B
Câu 3: D
Câu 4: A
Câu 5: C
Câu 6: B
Câu 7: A
Câu 9: B
Đúng 1
Bình luận (0)
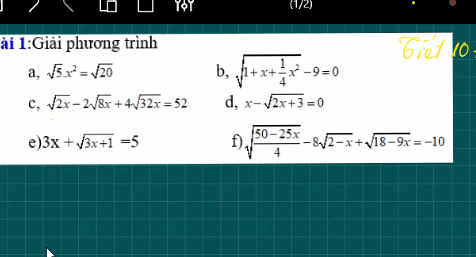
mọi người giải hộ e vs ạ!! em đg cần gấp,cảm ơn ạ :333
a) \(\Leftrightarrow x^2=\sqrt{4}\)
\(\Leftrightarrow x^2=2\Leftrightarrow x=\pm2\)
b) \(\Leftrightarrow\sqrt{\left(\dfrac{1}{2}x+1\right)^2}=9\)
\(\Leftrightarrow\left|\dfrac{1}{2}x+1\right|=9\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}x+1=9\\\dfrac{1}{2}x+1=-9\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=16\\x=-16\end{matrix}\right.\)
c) \(\Leftrightarrow\sqrt{2x}-4\sqrt{2x}+16\sqrt{2x}=52\left(đk:x\ge0\right)\)
\(\Leftrightarrow13\sqrt{2x}=52\Leftrightarrow\sqrt{2x}=4\Leftrightarrow2x=16\Leftrightarrow x=8\left(tm\right)\)
Đúng 0
Bình luận (0)
f: Ta có: \(\sqrt{\dfrac{50-25x}{4}}-8\sqrt{2-x}+\sqrt{18-9x}=-10\)
\(\Leftrightarrow\sqrt{2-x}\cdot\dfrac{5}{2}-8\sqrt{2-x}+3\sqrt{2-x}=-10\)
\(\Leftrightarrow\sqrt{2-x}=4\)
\(\Leftrightarrow2-x=16\)
hay x=-14
Đúng 0
Bình luận (0)
mọi người giải giúp em vs ạ em cần gấp
em cảm ơn mọi người nhiều


Khoảng cách từ M để ABC bằng MA
Khoảng cách từ EF đến SAB bằng EM = AF
Đúng 0
Bình luận (0)
Xin nhờ mọi người giải giúp em 2 bài này với ạ. Em cảm ơn thật nhiều.
Đọc tiếp
Xin nhờ mọi người giải giúp em 2 bài này với ạ. Em cảm ơn thật nhiều.
\(A=\dfrac{\sqrt{20}-6}{\sqrt{14-6\sqrt{5}}}-\dfrac{\sqrt{20}-\sqrt{28}}{\sqrt{12-2\sqrt{35}}}=\dfrac{-2\left(3-\sqrt{5}\right)}{\sqrt{\left(3-\sqrt{5}\right)^2}}+\dfrac{2\left(\sqrt{7}-\sqrt{5}\right)}{\sqrt{\left(\sqrt{7}-\sqrt{5}\right)^2}}\)
\(=\dfrac{-2\left(3-\sqrt{5}\right)}{3-\sqrt{5}}+\dfrac{2\left(\sqrt{7}-\sqrt{5}\right)}{\sqrt{7}-\sqrt{5}}=-2+2=0\)
\(B=\sqrt{\dfrac{\left(9-4\sqrt{3}\right)\left(6-\sqrt{3}\right)}{\left(6-\sqrt{3}\right)\left(6+\sqrt{3}\right)}}-\sqrt{\dfrac{\left(3+4\sqrt{3}\right)\left(5\sqrt{3}+6\right)}{\left(5\sqrt{3}-6\right)\left(5\sqrt{3}+6\right)}}\)
\(=\sqrt{\dfrac{66-33\sqrt{3}}{33}}-\sqrt{\dfrac{78+39\sqrt{3}}{39}}=\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{4-2\sqrt{3}}-\sqrt{4+2\sqrt{3}}\right)=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{\left(\sqrt{3}+1\right)^2}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{3}-1-\sqrt{3}-1\right)=-\sqrt{2}\)
Đúng 4
Bình luận (0)
a) Ta có: \(A=\dfrac{\sqrt{10}-3\sqrt{2}}{\sqrt{7-3\sqrt{5}}}-\dfrac{\sqrt{10}-\sqrt{14}}{\sqrt{6-\sqrt{35}}}\)
\(=\dfrac{2\sqrt{5}-6}{3-\sqrt{5}}-\dfrac{2\sqrt{5}-2\sqrt{7}}{\sqrt{7}-\sqrt{5}}\)
\(=\dfrac{\left(2\sqrt{5}-6\right)\left(3+\sqrt{5}\right)}{4}-\dfrac{\left(2\sqrt{5}-2\sqrt{7}\right)\left(\sqrt{7}+\sqrt{5}\right)}{2}\)
\(=\dfrac{\left(\sqrt{5}-3\right)\left(3+\sqrt{5}\right)-\left(2\sqrt{5}-2\sqrt{7}\right)\left(\sqrt{7}+\sqrt{5}\right)}{2}\)
\(=\dfrac{5-9-2\left(5-7\right)}{2}\)
\(=\dfrac{-4-2\cdot\left(-2\right)}{2}\)
\(=0\)
Đúng 1
Bình luận (0)

 * Mọi người cố giúp em hoàn thiện trong buổi tối nay với ạ, em đg cần gấp! Cảm ơn ạ!
* Mọi người cố giúp em hoàn thiện trong buổi tối nay với ạ, em đg cần gấp! Cảm ơn ạ!
12:
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
=>ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
b: Xét ΔNAC và ΔNBE có
góc NAC=góc NBE
NA=NB
góc ANC=góc BNE
=>ΔNAC=ΔNBE
=>AC=BE
c: Xét tứ giác AEBC có
AC//BE
AC=BE
=>AEBC là hình bình hành
=>AE//BC
d: Xét ΔEAC có EF/EA=EN/EC
nên FN//AC//EB
Xét ΔECB có CM/CB=CN/CE
nên NM//EB
=>F,N,M thẳng hàng
Đúng 1
Bình luận (0)
Mọi người giải giúp em với, em cần gấp ạ, em cảm ơn mọi người
-Bài 3:
2) -Áp dụng BĐT Caushy Schwarz ta có:
\(A=\dfrac{1}{x^3+3xy^2}+\dfrac{1}{y^3+3x^2y}\ge\dfrac{\left(1+1\right)^2}{x^3+3xy^2+3x^2y+y^3}=\dfrac{4}{\left(x+y\right)^3}\ge\dfrac{4}{1^3}=4\)-Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)
Đúng 0
Bình luận (0)





















