Cho tam giác ABC nhọn có 2 đường cao BD,CE cắt nhau ở H. Chứng minh
a, Tam giác ABC đồng dạng với tam giác AEC

b, AE.AB=AD.AC
c, tam giác ADE đồng dạng với tam giác ABC
d, Gọi I là hình chiếu của H trên BC. Chứng minh: BE,CD,HI đồng duy ( A,H,I thẳng hàng)

e, BH.BD + CH.CE=BC^2

f, DH là phân giác của góc EDI

g, AI.HK=AK.HI

h, HI/AI + HD/BD + HE/CE =1

i, Tính : AH/AI + BH/BD + CH/CE (=2)

 MỌI NGƯỜI GIÚP EM VỚI Ạ ( CHỈ CẦN CÂU f,g,h,i thôi ạ) 

Nếu không biết trân trọng kỉ niệm và kí ức thì con người phải đối mặt với hậu quả gì?

=5^5 -5^4+5^3=5^3.5^2 -5^3.5+5^3 
=5^3(5^2-5+1)=5^3.21 
Vì 21 chia hết cho 7 =>5^3.21 chia hết cho 7 
Vậy 5^5 -5^4+5^3 chia hết cho 7

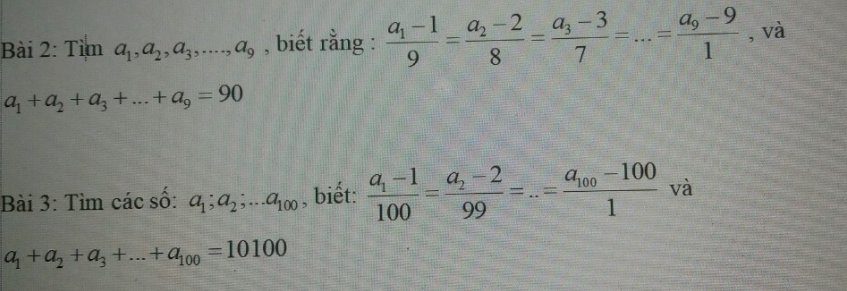
* Mọi người cố giúp em hoàn thiện trong buổi tối nay với ạ, em đg cần gấp! Cảm ơn ạ!

Bài 1: 

Cho tam giác ABC vuông tại B, vẽ AD là phân giác của góc BAC (D thuộc BC). Từ D kẻ DE vuông góc với AC (E thuộc AC). Gọi F là giao điểm của DE và AB 

a, CM: Tam giác ABE cân

b, CM: tam giác ADF = tam giác ADC

c, CM: BA + BC > DE + AC 

Cho tam giác ABC có AB<AC. Kẻ phân giác AD của góc BAC (D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE=AB

a, CM: DB=DE 

b, Trên tia AB lấy điểm F sao cho AF=AC. Gọi H là giao điểm của AD và CF. CM: AH vuông góc với FC

c, CM: 3 điểm E,D,F thẳng hàng

                      Giúp em với,em đang cần gấp ạ