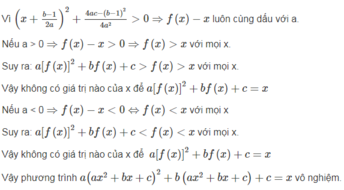cho a,b,c là 3 cạnh của 1 tam giác.chứng minh pt vô nghiệm (x2+ax+b)(x2+bx+a)=0

Những câu hỏi liên quan
Cho phương trình ax^2 +bx + c = 0 (a khác 0) và a - b + c = 0
a) Chứng tỏ x1 = -1 là 1 nghiệm của pt
b) Dùng định lý Viet về tích 2 nghiệm để tìm x2
Cảm ơn mb <3
Chứng minh rằng nếu phương trình a
x
2
+ bx + c x (a
≠
0) vô nghiệm thì phương trình a
a
x
2
+
b
x
+
c
2
+ b(a...
Đọc tiếp
Chứng minh rằng nếu phương trình a x 2 + bx + c = x (a ≠ 0) vô nghiệm thì phương trình a a x 2 + b x + c 2 + b(a x 2 + bx + c) + c = x cũng vô nghiệm.
cho pt: \(ax^2+by+c=0\)
và pt: \(cx^2+by+a=0\) (a\(\ne\)c)
2 pt trên có 1 nghiệm chung duy nhất
gọi x1,x2 lần lượt là 2 nghiệm còn lại của 2 pt trên
chứng minh \(\left|x1\right|+\left|x2\right|>2\)
giúp :))))
\(\left\{{}\begin{matrix}ax^2+by+c=0\\cx^2+by+a=0\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}ax^2+by=-c\\cx^2+by=-a\end{matrix}\right.\)
vì pt có 1 nghiệm duy nhất
nên\(\dfrac{a}{c}\ne\dfrac{b}{b}\)⇔\(\dfrac{a}{c}\ne1\)⇔\(a\ne c\)
Đúng 0
Bình luận (4)
Mình nghĩ là sai đề
Cho pt \(ax^2+bx+c=0\) (1) và \(cx^2+bx+a=0\) (2)
Lấy (1) trừ (2) ta được: \(\left(x^2-1\right)\left(a-c\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)(vì a khác c)
TH1: Giả sử nghiệm chung của hai pt là x=1
Thay x=1 vào (1) và (2) được: \(\left\{{}\begin{matrix}a+b+c=0\\a+b+c=0\end{matrix}\right.\)\(\Leftrightarrow b=-a-c\)
Áp dụng hệ thức viet vào hai pt:
\(\left\{{}\begin{matrix}x_1+1=-\dfrac{b}{a}\\x_2+1=-\dfrac{b}{c}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{b}{a}-1\\x_2=-\dfrac{b}{c}-1\end{matrix}\right.\)
Có: \(\left|x_1\right|+\left|x_2\right|>2\Leftrightarrow\left|-\dfrac{b}{a}-1\right|+\left|\dfrac{-b}{c}-1\right|>2\)
\(\Leftrightarrow\left|-\dfrac{-a-c}{a}-1\right|+\left|\dfrac{-\left(-a-c\right)}{c}-1\right|>2\)
\(\Leftrightarrow\left|\dfrac{c}{a}\right|+\left|\dfrac{a}{c}\right|>2\) \(\Leftrightarrow c^2+a^2>2\left|ac\right|\) (luôn đúng với mọi \(a\ne c\))
TH2: Giả sử x=-1 là nghiệm chung của hai pt
Thay x=-1 vào hai pt được: \(\left\{{}\begin{matrix}a-b+c=0\\c-b+a=0\end{matrix}\right.\) \(\Leftrightarrow b=a+c\)
Áp dụng viet vào hai pt có: \(\left\{{}\begin{matrix}x_1+\left(-1\right)=-\dfrac{b}{a}\\x_2+\left(-1\right)=-\dfrac{b}{c}\end{matrix}\right.\)
Khi đó: \(\left|x_1\right|+\left|x_2\right|=\left|-\dfrac{b}{a}+1\right|+\left|-\dfrac{b}{c}+1\right|\)
\(=\left|-\dfrac{a+c}{a}+1\right|+\left|-\dfrac{a+c}{c}+1\right|\)\(=\left|-\dfrac{c}{a}\right|+\left|-\dfrac{a}{c}\right|\)\(=\left|\dfrac{c}{a}\right|+\left|\dfrac{a}{c}\right|=\dfrac{c^2+a^2}{\left|ac\right|}>\dfrac{2\left|ac\right|}{\left|ac\right|}=2\)
Vậy...
Đúng 0
Bình luận (1)
Cho phương trình ax^2 + bx + c = 0(a ≠ 0) có hai nghiệm phân biệt x1, x2
thoả mãn x1 =x2^2 . Chứng minh b^3 + a^2c + ac^2 = 3abc
Cho phương trình ax^2 + bx + c = 0(a ≠ 0) có hai nghiệm phân biệt x1, x2
thoả mãn x1 =x2^2 . Chứng minh b^3 + a^2c + ac^2 = 3abc .
Cho pt bậc 2 ẩn x: x2 + 3x + m = 0. a) Giải pt (1) khi m = 0; m = -4. b) Tìm m để pt (1) vô nghiệm. c) Tìm m để pt (1) có một nghiệm là -1. Tìm nghiệm kia. d) Cho x1, x2 là 2 nghiệm của pt (1). Không giải pt, hãy tìm giá trị của m để: 1/ x1^2 + x2^2=34 2/ x1 - x2=6 3/ x1=2x2 4/ 3x1+2x2=20 5/ x1^2-x2^2=30.
a.Bạn thế vào nhé
b.\(\Delta=3^2-4m=9-4m\)
Để pt vô nghiệm thì \(\Delta< 0\)
\(\Leftrightarrow9-4m< 0\Leftrightarrow m>\dfrac{9}{4}\)
c.Ta có: \(x_1=-1\)
\(\Rightarrow x_2=-\dfrac{c}{a}=-m\)
d.Theo hệ thức Vi-ét, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-3\\x_1.x_2=m\end{matrix}\right.\)
1/ \(x_1^2+x_2^2=34\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=34\)
\(\Leftrightarrow\left(-3\right)^2-2m=34\)
\(\Leftrightarrow m=-12,5\)
..... ( Các bài kia tương tự bạn nhé )
Đúng 2
Bình luận (0)
cho pt bậc 2 : ax^2+bx+c=0 có 2 nghiệm phân biệt thỏa mãn
X1+x2-2.X1x2=0
mx1x2-(x1+x2)=2m+1
a) tìm pt bậc hai trên với m là tham số
b)xác định m để phương trình bậc 2 trên có 2 nghiệm dương phân biệt
viết lại câu hỏi khác đi, đề không rõ ràng X với x rồi . lung tung, dung công cụ soạn thảo đi nha bạn
Đúng 0
Bình luận (0)
cho x1, x2 là 2 nghiệm dương của phương trình ax^2+bx+c=0
chứng minh phương trình cx^2+ax+b=0 cũng có 2 nghiệm dương x3,x4 và x1+x2+x3+x4>4 ?
a) ax^2 + bx + c = 0
Để phương trình thỏa mãn điều kiện có 2 nghiệm dương phân biệt.
∆ > 0
=> b^2 - 4ac > 0
x1 + x2 = -b/a > 0
=> b và a trái dấu
x1.x2 = c/a > 0
=> c và a cùng dấu
Từ đó ta xét phương trình cx^2 + bx^2 + a = 0
∆ = b^2 - 4ac >0
x3 + x4 = -b/c, vì a và c cùng dấu mà b và a trái dấu nên b và c trái dấu , vì vậy -b/c >0
x3.x4 = a/c, vì a và c cùng dấu nên a/c > 0
=> phương trình cx^2 + cx + a có 2 nghiệm dương phân biệt x3 và x4
Vậy nếu phương trình ax^2 + bx + c = 0 có 2 nghiệm dương phân biệt thì phương trình cx^2 + bx + a = 0 cũng có 2 nghiệm dương phân biệt.
b) Ta có, vì x1, x2, x3, x4 không âm, dùng cô si.
x1 + x2 ≥ 2√( x1.x2 )
x3 + x4 ≥ 2√( x3x4 )
=> x1 + x2 + x3 + x4 ≥ 2[ √( x1.x2 ) + √( x3x4 ) ] (#)
Tiếp tục côsi cho 2 số không âm ta có
√( x1.x2 ) + √( x3x4 ) ≥ 2√[√( x1.x2 )( x3.x4 ) ] (##)
Theo a ta có
x1.x2 = c/a
x3.x4 = a/c
=> ( x1.x2 )( x3.x4 ) = 1
=> 2√[√( x1.x2 )( x3.x4 ) ] = 2
Từ (#) và (##) ta có
x1 + x2 + x3 + x4 ≥ 4
Đúng 0
Bình luận (0)
Cho pt : x2 - 2(m-3) x + m2 - 1 = 0 ( m là tham số ). Tìm m để pt : a) vô nghiêm b) có nghiệm c) có nghiệm kép. Tìm nghiệm kép d) có 2 nghiệm phân biệt
Ta có: \(\Delta=4\left(m-3\right)^2-4.\left(m^2-1\right)\)
a. Để phương trình vô nghiệm thì \(\Delta< 0\Leftrightarrow\left(m-3\right)^2< m^2-1\Leftrightarrow m^2-6m+9< m^2-1\Leftrightarrow6m>10\Leftrightarrow m>\dfrac{10}{6}=\dfrac{5}{3}\)
b. Để phương trình có nghiệm thì:
\(\Delta\ge0\Leftrightarrow\left(m-3\right)^2\ge m^2-1\Leftrightarrow m^2-6m+9\ge m^2-1\Leftrightarrow6m\le10\Leftrightarrow m\le\dfrac{10}{6}=\dfrac{5}{3}\)
c. Để phương trình có nghiệm kép thì:
\(\Delta=0\Leftrightarrow\left(m-3\right)^2=m^2-1\Leftrightarrow m^2-6m+9=m^2-1\Leftrightarrow6m=10\Leftrightarrow m=\dfrac{10}{6}=\dfrac{5}{3}\)
Nghiệm kép của phương trình là: \(\dfrac{-b}{2a}=\dfrac{2\left(m-3\right)}{2.1}=\dfrac{2\left(\dfrac{5}{3}-3\right)}{2}=-\dfrac{4}{3}\)
d. Để phương trình có nghiệm phân biệt thì:
\(\Delta>0\Leftrightarrow\left(m-3\right)^2>m^2-1\Leftrightarrow m^2-6m+9>m^2-1\Leftrightarrow6m< 10\Leftrightarrow m< \dfrac{10}{6}=\dfrac{5}{3}\)
Đúng 2
Bình luận (0)
a, Để pt vô nghiệm
\(\Delta'=\left(m-3\right)^2-\left(m^2-1\right)=-6m+9+1=-6m+10< 0\Leftrightarrow m>\dfrac{5}{3}\)
b, Để pt có nghiệm
\(\Delta'=-6m+10\ge0\Leftrightarrow m\le\dfrac{5}{3}\)
c, Để pt có nghiệm kép
\(\Delta'=-6m+10=0\Leftrightarrow m=\dfrac{5}{3}\)
\(x_1=x_2=\dfrac{2\left(m-3\right)}{2}=m-3\)
d, Để pt có 2 nghiệm pb
\(\Delta=-6m+10>0\Leftrightarrow m< \dfrac{5}{3}\)
Đúng 0
Bình luận (0)