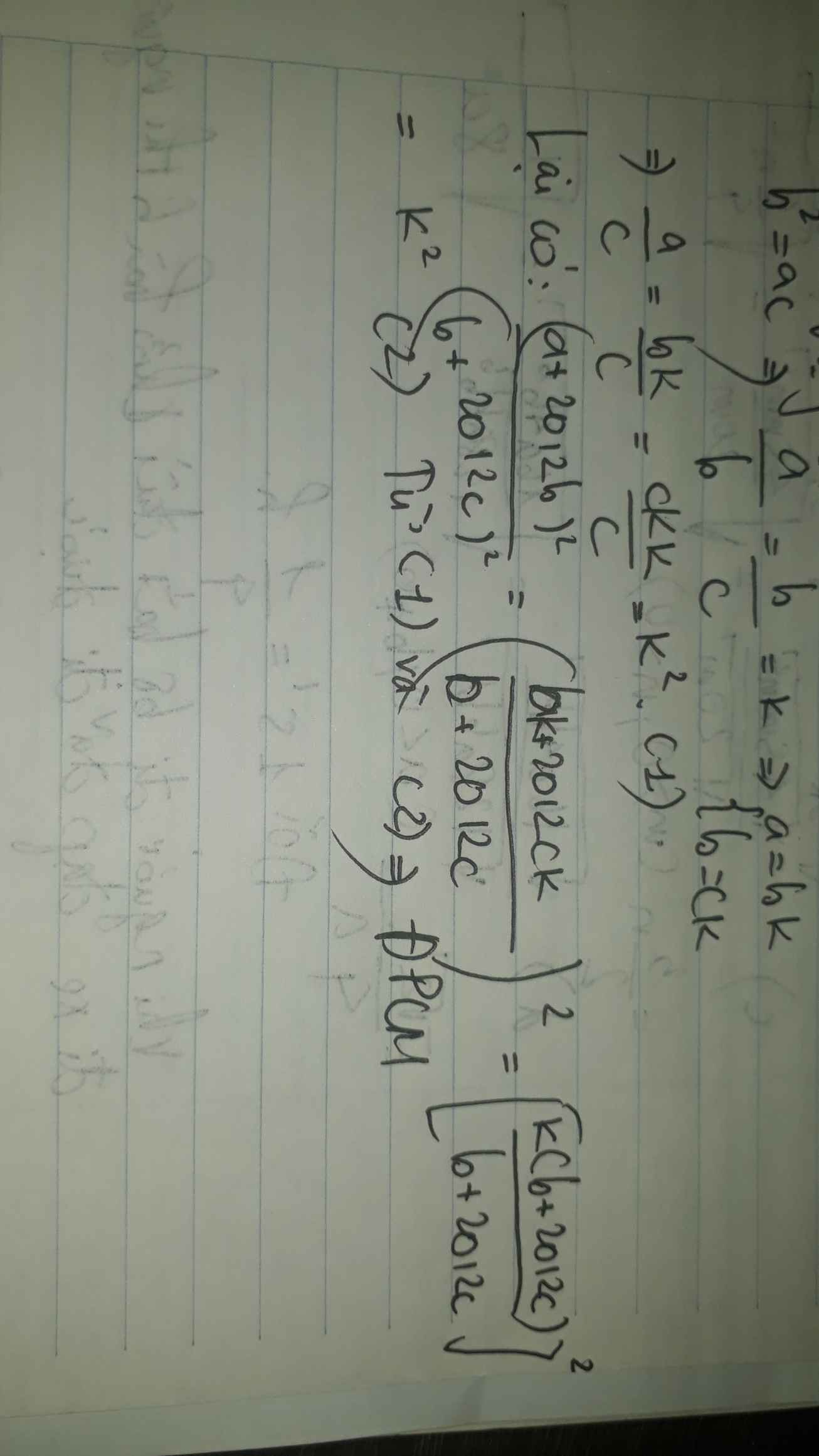cho các số a,b,c khác 0 và thảo mãn b^2=ac. chứng minh a/c=(a+2013b)^2/(b+2013c)^2

Những câu hỏi liên quan
Cho các số a, b, c khác 0 thỏa mãn: \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=0\)
Tính \(S=\dfrac{2013a^2-2014}{a^2+2bc}+\dfrac{2013b^2-2014}{b^2+2ca}+\dfrac{2013c^2-2014}{c^2+2ab}\)
Ta có kết quả tổng quát hơn như sau:
Cho $a,b,c \neq 0$ thỏa mãn $\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=0.$
Chứng minh rằng $$S={\frac {k{a}^{2}-k-1}{{a}^{2}+2\,bc}}+{\frac {{b}^{2}k-k-1}{2\,ac+{b}^{2}}}+{\frac {{c}^{2}k-k-1}{2\,ab+{c}^{2}}}=k$$
Đúng 1
Bình luận (0)
1. Cho 2 đa thức:P(x)=3x3+x2-3x-1; Q(x)=-3x3-x2-x-15. Tìm x để P(x)=-Q(x)
2. Cho các số a,b,c đều khác 0 và thỏa mãn b2=ac. Chứng minh rằng: \(\frac{a}{b}=\frac{\left(a+2013b\right)^2}{\left(b+2013c\right)^2}\)
Để P(x)=Q(x) thì:\(3x^3+x^2-3x-1=-3x^3-x^2-x-15\)
Nếu \(3x^3+x^2-3x-1=-3x^3-x^2-x-15\)
=>\(\left(3x^3+x^2-3x-1\right)-\left(-3x^3-x^2-x-15\right)=0\)
=>\(3x^3+x^2-3x-1+3x^3+x^2+x+15=0\)
=>\(\left(3x^3+3x^3\right)+\left(x^2+x^2\right)+\left(-3x+x\right)+\left(-1+15\right)=0\)
=>\(6x^3+2x^2-2x+14=0\)
=>\(6x^3+2x^2-2x=-14\)
Đúng 0
Bình luận (0)
Cho các số thực a, b, c khác 0 thảo mãn: a + b + c, a^2 + b^2 + c^2 = 4 và x/a = y/b = z/c. Chứng minh rằng x*y + y*z + z*x = 0
Cho ba số a,b,c khác 0 thỏa mãn b2 = ac và c2 = ab
a) Chứng minh rằng a+b+c khác 0
b) So sánh các số a, b và c
cho các số khác 0 là a;b;c thõa mãn b^2=ac. Chứng minh: a/c=(a+2015b)^2/(b+2015c)^2
Chứng minh 2013 < \(\dfrac{2013a}{a+b+c}+\dfrac{2013b}{b+c+d}+\dfrac{2013c}{c+d+a}+\dfrac{2013d}{d+a+b}< 4026\)
Cho a,b,c thuộc R và a,b,c khác 0 thỏa mãn b^2=ac. chứng minh rằng a/c=(a+2012b)^2/(b+2012c)^2
A)23/42-10/21
B)16/25-3/15
C)7/8-1/3-1/2
D)15/7-4/9-10/9
Đúng 1
Bình luận (0)
Vì \(b^2=ac\) ta suy ra \(\dfrac{a}{b}=\dfrac{b}{c}\). Đặt \(a=kb\) và \(b=kc\).
Khi đó \(\dfrac{a}{c}=\dfrac{k\left(kc\right)}{c}=k^2\). (1)
Từ tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{2012b}{2012c}=\dfrac{a+2012b}{b+2012c}=k\), suy ra \(k^2=\dfrac{\left(a+2012b\right)^2}{\left(b+2012c\right)^2}\). (2)
Từ (1) và (2) suy ra \(k^2=\dfrac{a}{c}=\dfrac{\left(a+2012b\right)^2}{\left(b+2012c\right)^2}\) (đpcm)
Đúng 1
Bình luận (0)
cho 3 số thực a, b, c>0 thỏa mãn a+b+c=2013
cm:
\(\frac{a}{a+\sqrt{2013a+bc}}+\frac{b}{b+\sqrt{2013b+ac}}+\frac{c}{c+\sqrt{2013c+ab}}\le1\)
Ta có : \(\frac{a}{a+\sqrt{2013a+bc}}=\frac{a}{a+\sqrt{a^2+ab+ac+bc}}=\frac{a}{a+\sqrt{\left(a+b\right)\left(a+c\right)}}\)
Theo bất đẳng thức Bunhiacopxki : \(\sqrt{\left(a+b\right)\left(c+a\right)}\ge\sqrt{\left(\sqrt{ac}+\sqrt{ab}\right)^2}=\sqrt{ab}+\sqrt{ac}\)
\(\Rightarrow\frac{a}{a+\sqrt{\left(a+b\right)\left(a+c\right)}}\le\frac{a}{a+\sqrt{ab}+\sqrt{ac}}=\frac{\sqrt{a}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
hay \(\frac{a}{a+\sqrt{2013a+bc}}\le\frac{\sqrt{a}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
Tương tự : \(\frac{b}{b+\sqrt{2013b+ac}}\le\frac{\sqrt{b}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
\(\frac{c}{c+\sqrt{2013c+ab}}\le\frac{\sqrt{c}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
Cộng các bất đẳng thức trên theo vế được \(\frac{a}{a+\sqrt{2013a+bc}}+\frac{b}{b+\sqrt{2013b+ac}}+\frac{c}{c+\sqrt{2013c+ab}}\le1\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}\frac{a}{b}=\frac{b}{c}=\frac{c}{a}\\a+b+c=2013\\a,b,c>0\end{cases}}\) \(\Leftrightarrow a=b=c=671\)
Đúng 0
Bình luận (0)
: Cho a,b,c thuộc R và a,b,c khác 0 thoả mãn b2 = ac. Chứng minh rằng:
a/c=(a+2012b)^2/(b+2012c)2