Giúp mình từ bài 26 đến hết ạh

Những câu hỏi liên quan
Mọi người giúp mình bài này với ạh,cảm ơn mn
Phân tích đa thức thành nhân tử
1)x3 + 3x2 - 16x - 48
2)4x(x - 3y) + 12y(3y - x)
3)x3 + 2x2 - 2x - 1
mong mn giúp mình với ạh!Cảm ơn nhiều lắm ạh!🥺🥺
Lời giải:
1.
$x^3+3x^2-16x-48=(x^3+3x^2)-(16x+48)=x^2(x+3)-16(x+3)$
$=(x+3)(x^2-16)=(x+3)(x-4)(x+4)$
2.
$4x(x-3y)+12y(3y-x)=4x(x-3y)-12y(x-3y)=(x-3y)(4x-12y)=4(x-3y)(x-3y)=4(x-3y)^2$
3.
$x^3+2x^2-2x-1=(x^3-x^2)+(3x^2-3x)+(x-1)=x^2(x-1)+3x(x-1)+(x-1)$
$=(x-1)(x^2+3x+1)$
Đúng 3
Bình luận (0)
Giúp mình từ bài 2.8 đến hết bài 3 nhé mình cảm ơn
III:
1) \(x-y=\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)\)
2) \(x-1=\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\)
4) \(a-2\sqrt{a}+1=\left(\sqrt{a}-1\right)^2\)
5) \(2x-\sqrt{x}-3=\left(\sqrt{x}+1\right)\left(2\sqrt{x}-3\right)\)
6) \(6a^2-5a\sqrt{b}-b=\left(a-\sqrt{b}\right)\left(6a+\sqrt{b}\right)\)
7) \(x-2\sqrt{x-1}-y^2=\left(\sqrt{x-1}-1\right)^2-y^2=\left(\sqrt{x-1}-1-y\right)\left(\sqrt{x-1}-1+y\right)\)
Đúng 2
Bình luận (1)
II:
2.8) ĐKXĐ: \(x\ge2\)
2.9: ĐKXĐ: \(\left[{}\begin{matrix}x< \dfrac{1}{2}\\\dfrac{1}{2}< x\le1\end{matrix}\right.\)
2.10: ĐKXĐ: \(x\ne0\)
2.11: ĐKXĐ: \(\left[{}\begin{matrix}x\le-5\\x\ge3\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Một căn phòng hình chữ nhật có diện tích gấp đôi căn phòng hình vuông có cạnh 9m. Tính số viên gạch cần lát hết căn phòng.
Mọi người cho mình hỏi để bài này đúng hay bị thiếu ạh ? Nếu đề bài đúng các bạn giải giúp mình nhanh nhanh , ngày mai mình đi học rồi
GIÚP MÌNH TỪ CÂU 26 ĐẾN 30 VỚI

1 It was silly to lend him money
2 Meeting the president is exciting
3 While we were on the summer holiday, we were so happy
4 While they were playing, they cried twice
5 Writing good composition in English was not easy
Đúng 2
Bình luận (0)
GIÚP MÌNH TỪ CÂU 26 ĐẾN 30 VỚI

26 It was silly to lend him money
27 Meeting the president is exciting
28 While we were in the summer holiday, we were happy
29 While the play was being played, they cried twice
30 Writing good compositions in English was not easy
Đúng 0
Bình luận (0)
Giúp mình là từ câu 18 đến 26 với mình cảm ơn nhiều

18.
Áp dụng BĐT quen thuộc: \(\dfrac{1}{1+x^2}+\dfrac{1}{1+y^2}\ge\dfrac{2}{1+xy}\) ta có:
\(\dfrac{1}{1+a^3}+\dfrac{1}{1+b^3}\ge\dfrac{2}{1+\sqrt{a^3b^3}}\) ; \(\dfrac{1}{1+c^3}+\dfrac{1}{1+abc}\ge\dfrac{2}{1+\sqrt{abc^4}}\)
Cộng vế:
\(\dfrac{1}{1+a^3}+\dfrac{1}{1+b^3}+\dfrac{1}{1+c^3}+\dfrac{1}{1+abc}\ge2\left(\dfrac{1}{1+\sqrt{a^3b^3}}+\dfrac{1}{1+\sqrt{abc^4}}\right)\ge2\left(\dfrac{2}{1+\sqrt[4]{a^4b^4c^4}}\right)\)
\(\Rightarrow\dfrac{1}{1+a^3}+\dfrac{1}{1+b^3}+\dfrac{1}{1+c^3}+\dfrac{1}{1+abc}\ge\dfrac{4}{1+abc}\)
\(\Rightarrow\dfrac{1}{1+a^3}+\dfrac{1}{1+b^3}+\dfrac{1}{1+c^3}\ge\dfrac{3}{1+abc}\) (đpcm)
Đúng 1
Bình luận (1)
19.
Biến đổi tương đương:
\(\Leftrightarrow\left(a^2+b^2\right)xy+ab\left(x^2+y^2\right)\ge\left(a^2+b^2+2ab\right)xy\)
\(\Leftrightarrow\left(a^2+b^2\right)xy+ab\left(x^2+y^2\right)\ge\left(a^2+b^2\right)xy+2abxy\)
\(\Leftrightarrow ab\left(x^2+y^2\right)-2abxy\ge0\)
\(\Leftrightarrow ab\left(x^2+y^2-2xy\right)\ge0\)
\(\Leftrightarrow ab\left(x-y\right)^2\ge0\)
Đúng 1
Bình luận (1)
20.
\(\Leftrightarrow a+b+c\ge\dfrac{3\left(ab+bc+ca\right)}{abc}\)
\(\Leftrightarrow a+b+c\ge\dfrac{3\left(ab+bc+ca\right)}{a+b+c}\) (do \(abc=a+b+c\))
\(\Leftrightarrow\left(a+b+c\right)^2\ge3\left(ab+bc+ca\right)\)
\(\Leftrightarrow a^2+b^2+c^2\ge ab+bc+ca\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ac\ge0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\) (luôn đúng)
Đúng 1
Bình luận (3)
Xem thêm câu trả lời
Lm bài 2 giúp e ạh 
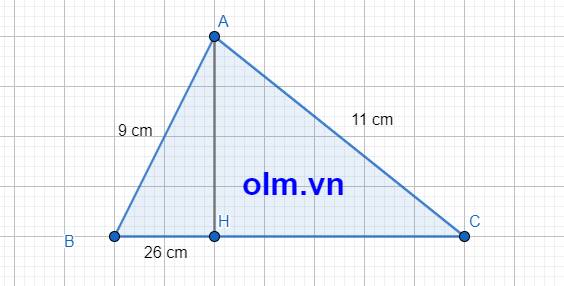
Cho tam giác ABC có AB bằng 9cm; ac bằng 11cm. Kẻ đường cao AH, biết BH bằng 26cm. Tính CH?
Mọi người giúp mình bài này với,mình cảm ơn nhiều!
(Không cần vẽ hình đâu ạh!)
Vì AH là đường cao của tam giác ABC nên AH \(\perp\) BC \(\equiv\) H
⇒ \(\Delta\) AHB \(\perp\) \(\equiv\) H \(\Rightarrow\) AB > BH ⇒ 9 cm > 26 cm vô lý
Em có hai sựa lựa chọn: 1 là em chỉ ra cái sai của cô
2 là em xem lại đề bài của em
Đúng 3
Bình luận (0)
Ta có :
\(AH^2=AB^2+BH^2\left(1\right)\) (Δ ABH vuông tại H)
\(AH^2=AC^2+CH^2\left(2\right)\) (Δ ACH vuông tại H)
\(\left(1\right),\left(2\right)\Rightarrow AB^2+BH^2=AC^2+CH^2\)
\(\Rightarrow CH^2=AB^2+BH^2-AC^2\)
\(\Rightarrow CH^2=81+676-121=636\)
\(\Rightarrow CH=\sqrt[]{636}=\sqrt[]{4.159}=2\sqrt[]{159}\left(cm\right)\)
Đúng 1
Bình luận (0)
Giúp mình câu 3 với ạh! Mình cảm ơn rất nhiều




















