a, - Xét phương trình hoành độ giao điểm :\(x^2=\left(m-2\right)x-m+3\)

\(\Leftrightarrow x^2-\left(m-2\right)x+m-3=0\left(I\right)\)

Có \(\Delta=b^2-4ac=\left(m-2\right)^2-4\left(m-3\right)\)

\(=m^2-4m+4-4m+12=m^2-8m+16=\left(m-4\right)^2\)

- Để P cắt d tại 2 điểm phân biệt <=> PT ( I ) có 2 nghiệm phân biệt .

<=> \(\Delta>0\)

\(\Leftrightarrow\left(m-4\right)^2>0\)

\(\Leftrightarrow m\ne4\)

Vậy ...

b, Hình như đề thiếu giá trị của cạnh huỳnh hay sao á :vvvv

a) Phương trình hoành độ giao điểm là: 

\(x^2=\left(m-2\right)x-m+3\)

\(\Leftrightarrow x^2-\left(m-2\right)x+m-3=0\)

\(\Delta=\left(m-2\right)^2-4\cdot\left(m-3\right)=m^2-4m+4-4m+12=m^2-8m+16\)

Để (d) cắt (P) tại hai điểm phân biệt thì \(\Delta>0\)

\(\Leftrightarrow m^2-8m+16>0\)

\(\Leftrightarrow\left(m-4\right)^2>0\)

mà \(\left(m-4\right)^2\ge0\forall m\)

nên \(m-4\ne0\)

hay \(m\ne4\)

Vậy: khi \(m\ne4\) thì (d) cắt (P) tại hai điểm phân biệt

- Thay x = -1 và x = 2 vào hàm số ( P ) ta được :

\(\left[{}\begin{matrix}y=1\\y=4\end{matrix}\right.\)

=> Đường thẳng AB đi qua 2 điểm ( -1; 1 ) ; ( 2 ; 4 )

- Gọi đường thẳng AB có dạng  y = ax + b

- Thay hai điểm trên lần lượt vào phương trình đường thẳng ta được :

\(\left\{{}\begin{matrix}-a+b=1\\2a+b=4\end{matrix}\right.\)

 \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\)

Vậy phương trình đường thẳng AB có dạng : y = x + 2 .

  =>y=2x+9

a: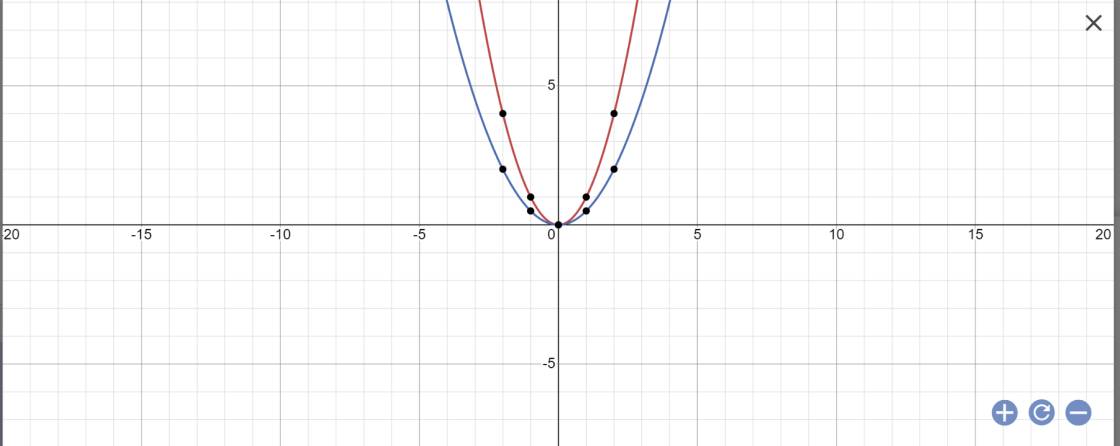 

b: Khi x=2 thì y=1/2*2^2=2

=>A(2;2)

Khi x=2 thì y=2^2=4

=>B(2;4)

c: Tọa độ A' là:

\(\left\{{}\begin{matrix}x_{A'}=-x_A=-2\\y_{A'}=y_A=2\end{matrix}\right.\)

Vì f(-2)=1/2*(-2)^2=2

nên A' thuộc (P1)

Tọa độ B' là:

\(\left\{{}\begin{matrix}x_{B'}=-x_B=-2\\y_{B'}=y_B=4\end{matrix}\right.\)

Vì f1(-2)=(-2)^2=4

nên B' thuộc y=x^2