 giúp với ét o ét
giúp với ét o ét

Những câu hỏi liên quan
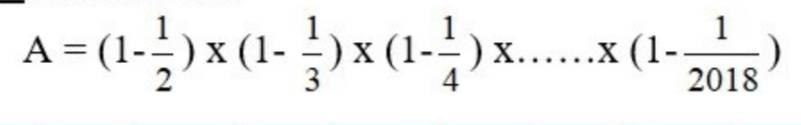 giúp mình với ét o ét
giúp mình với ét o ét
\(A=\dfrac{1.2.3...2017}{2.3.4...2018}=\dfrac{1}{2018}\)
Đúng 2
Bình luận (0)
Ét o ét giúp mik với ạaaaaa
Giúp muk với . Rõ ràng ra nhá. Ét o ét 
bài 1
a)\(=\dfrac{16}{40}+\dfrac{15}{40}=\dfrac{31}{40}\)
b)\(=\dfrac{7}{6}-\dfrac{4}{6}=\dfrac{3}{6}=\dfrac{1}{2}\)
c)\(=\dfrac{30}{9}=\dfrac{10}{3}\)
d)\(=\dfrac{8}{5}\times\dfrac{7}{4}=\dfrac{14}{5}\)
Đúng 4
Bình luận (0)
bài 1
a) 2/5 + 3/8 = 31/40
b) 7/6 - 2/3 = 1/2
c) 5/9 x 6 = 10/3
d) 8/5 : 4/7 = 14/5
Bài 2
a) 4/5 + x = 5/6
x = 5/6 - 4/5
x = 1/30
b) x : 7/10 = 5
x = 7/10 x 5
x = 7/2
Đúng 3
Bình luận (0)
bài 2
a)\(x=\dfrac{5}{6}-\dfrac{4}{5}=\dfrac{25}{30}-\dfrac{24}{30}=\dfrac{1}{30}\)
b)\(x=5:\dfrac{7}{10}=5\times\dfrac{10}{7}=\dfrac{50}{7}\)
Đúng 4
Bình luận (0)
Xem thêm câu trả lời
Ét O Ét, giúp mình câu a bài 4 với
\(\alpha\in\left(-90;0\right)\Rightarrow\left\{{}\begin{matrix}sina< 0\\cosa>0\end{matrix}\right.\) \(\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{3}{5}\)
\(cot\left(a+60^0\right)=\dfrac{cos\left(a+60^0\right)}{sin\left(a+60^0\right)}=\dfrac{cosa.cos60^0-sina.sin60^0}{sina.cos60^0+cosa.sin60^0}\)
\(=\dfrac{\dfrac{3}{5}.\dfrac{1}{2}-\left(-\dfrac{4}{5}\right).\dfrac{\sqrt{3}}{2}}{-\dfrac{4}{5}.\dfrac{1}{2}+\dfrac{3}{5}.\dfrac{\sqrt{3}}{2}}=...\)
\(sin\left(45^0-a\right)=sin45^0.cosa-cos45^0.sina=\dfrac{\sqrt{2}}{2}.\dfrac{3}{5}-\dfrac{\sqrt{2}}{2}.\left(-\dfrac{4}{5}\right)=...\)
Đúng 0
Bình luận (0)
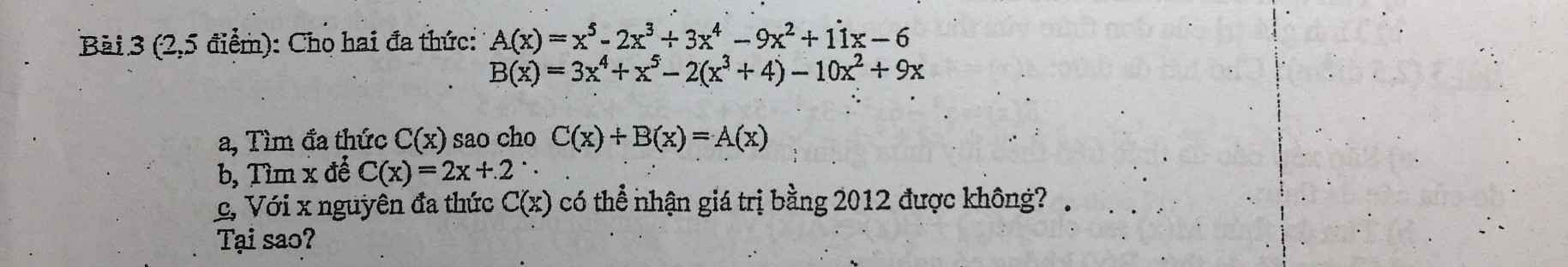 GIÚP MIK VỚI Ạ MIK CẦN GẤP !!! ÉT O ÉT
GIÚP MIK VỚI Ạ MIK CẦN GẤP !!! ÉT O ÉT
a: A(x)=x^5+3x^4-2x^3-9x^2+11x-6
B(x)=x^5+3x^4-2x^3-10x^2+9x-8
C(x)=A(x)-B(x)
=x^5+3x^4-2x^3-9x^2+11x-6-x^5-3x^4+2x^3+10x^2-9x+8
=x^2+2x+2
b; C(x)=2x+2
=>x^2=0
=>x=0
c: C(x)=2012
=>x^2+2x-2010=0
Δ=2^2-4*1*(-2010)=8044>0
=>Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-2-\sqrt{8044}}{2}\simeq-45,84\left(loại\right)\\x_2=\dfrac{-2+\sqrt{8044}}{2}\simeq43,84\left(loại\right)\end{matrix}\right.\)
=>Ko có giá trị nguyên của x thỏa mãn
Đúng 0
Bình luận (0)
Ét o ét , giúp mik với ạ . Mik cảm ưn🤧
31,5x0,1+Xx3=7,65
mn giúp mik với ét o ét cíuuuuuu
31,5 x 0,1 + x `3 = 7,65
3,15 + x 3 = 7,65
x 3 = 7,65 - 3,15
x 3 = 4,5
= 4,5 : 3
= 1,5
tick cho mik nha
Đúng 3
Bình luận (0)
`31.5xx0.1+x xx3=7.65`
`=> 3.15+x xx3=7.65`
`=> x xx3=7.65-3.15`
`=> x xx3=4.5`
`=> x=4.5:3`
`=> x=1.5`
Vậy `x=1.5`
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Ét O Ét, giúp e bagi 6 với 🙏🙏🙏🙏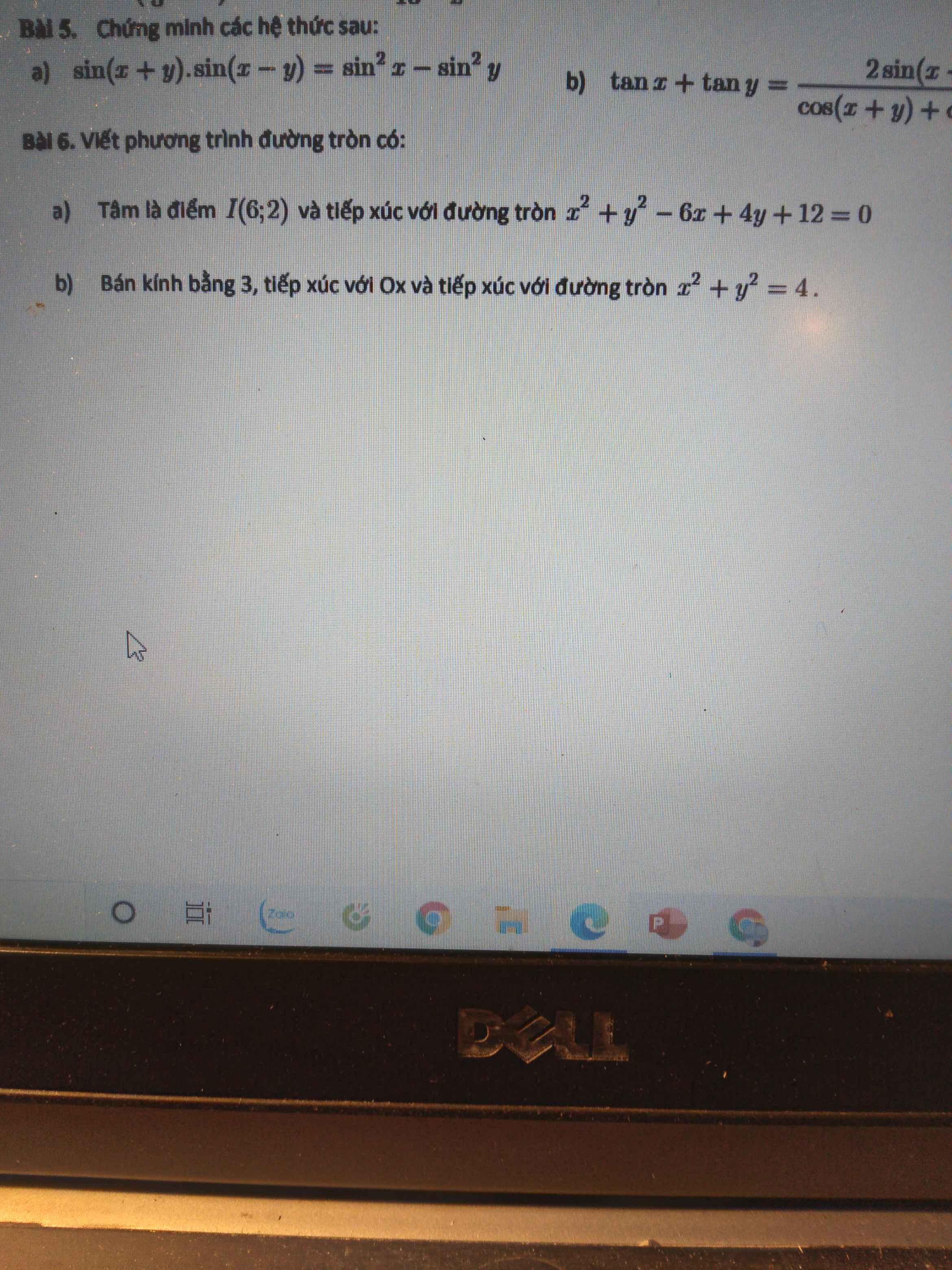
a.
Đường tròn (C): \(x^2+y^2-6x+4y+12=0\) có tâm \(J\left(3;-2\right)\) bán kính \(r=1\)
Tiếp điểm A của 2 đường tròn phải nằm trên đường nối tâm IJ
\(\overrightarrow{JI}=\left(3;4\right)\Rightarrow\) phương trình IJ có dạng:
\(4\left(x-3\right)-3\left(y+2\right)=0\Leftrightarrow4x-3y-18=0\)
Tọa độ tiếp điểm A là nghiệm của hệ :
\(\left\{{}\begin{matrix}4x-3y-18=0\\x^2+y^2-6x+4y+12=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{4x-18}{3}\\x^2+y^2-6x+4y+12=0\end{matrix}\right.\)
\(\Rightarrow x^2+\left(\dfrac{4x-18}{3}\right)^2-6x+4\left(\dfrac{4x-18}{3}\right)+12=0\)
\(\Rightarrow\dfrac{25}{9}x^2-\dfrac{50}{3}x+24=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{12}{5}\Rightarrow y=-\dfrac{14}{5}\\x=\dfrac{18}{5}\Rightarrow y=-\dfrac{6}{5}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}A\left(\dfrac{12}{5};-\dfrac{14}{5}\right)\\A\left(\dfrac{18}{5};-\dfrac{6}{5}\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\overrightarrow{AI}=\left(\dfrac{18}{5};\dfrac{24}{5}\right)\\\overrightarrow{AI}=\left(\dfrac{12}{5};\dfrac{16}{5}\right)\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}R^2=AI^2=36\\R^2=AI^2=\dfrac{36}{5}\end{matrix}\right.\)
Có 2 đường tròn thỏa mãn:
\(\left[{}\begin{matrix}\left(x-6\right)^2+\left(y-2\right)^2=36\\\left(x-6\right)^2+\left(y-2\right)^2=\dfrac{36}{5}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
b.
Đường tròn (C): \(x^2+y^2=4\) có tâm \(O\left(0;0\right)\) và bán kính \(r=2\)
Gọi \(I\left(a;b\right)\) là tâm của đường tròn (C') cần tìm
Do (C') tiếp xúc Ox \(\Rightarrow d\left(I;Ox\right)=3\Rightarrow\dfrac{\left|b\right|}{1}=3\Rightarrow b=\pm3\)
TH1: \(I\left(a;3\right)\Rightarrow\overrightarrow{OI}=\left(a;3\right)\Rightarrow OI=\sqrt{a^2+9}\)
Do 2 đường tròn tiếp xúc \(\Rightarrow\left[{}\begin{matrix}R+r=OI\\R-r=OI\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}OI=5\\OI=1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\sqrt{a^2+9}=5\\\sqrt{a^2+9}=1\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow a=\pm4\)
TH2: hoàn toàn tương tự ta có tìm được \(a=\pm4\)
Vậy có 4 đường tròn thỏa mãn: \(\left[{}\begin{matrix}\left(x-4\right)^2+\left(y-3\right)^2=9\\\left(x+4\right)^2+\left(y-3\right)^2=9\\\left(x-4\right)^2+\left(y+3\right)^2=9\\\left(x+4\right)^2+\left(y+3\right)^2=9\end{matrix}\right.\)
Đúng 2
Bình luận (0)






















