a.
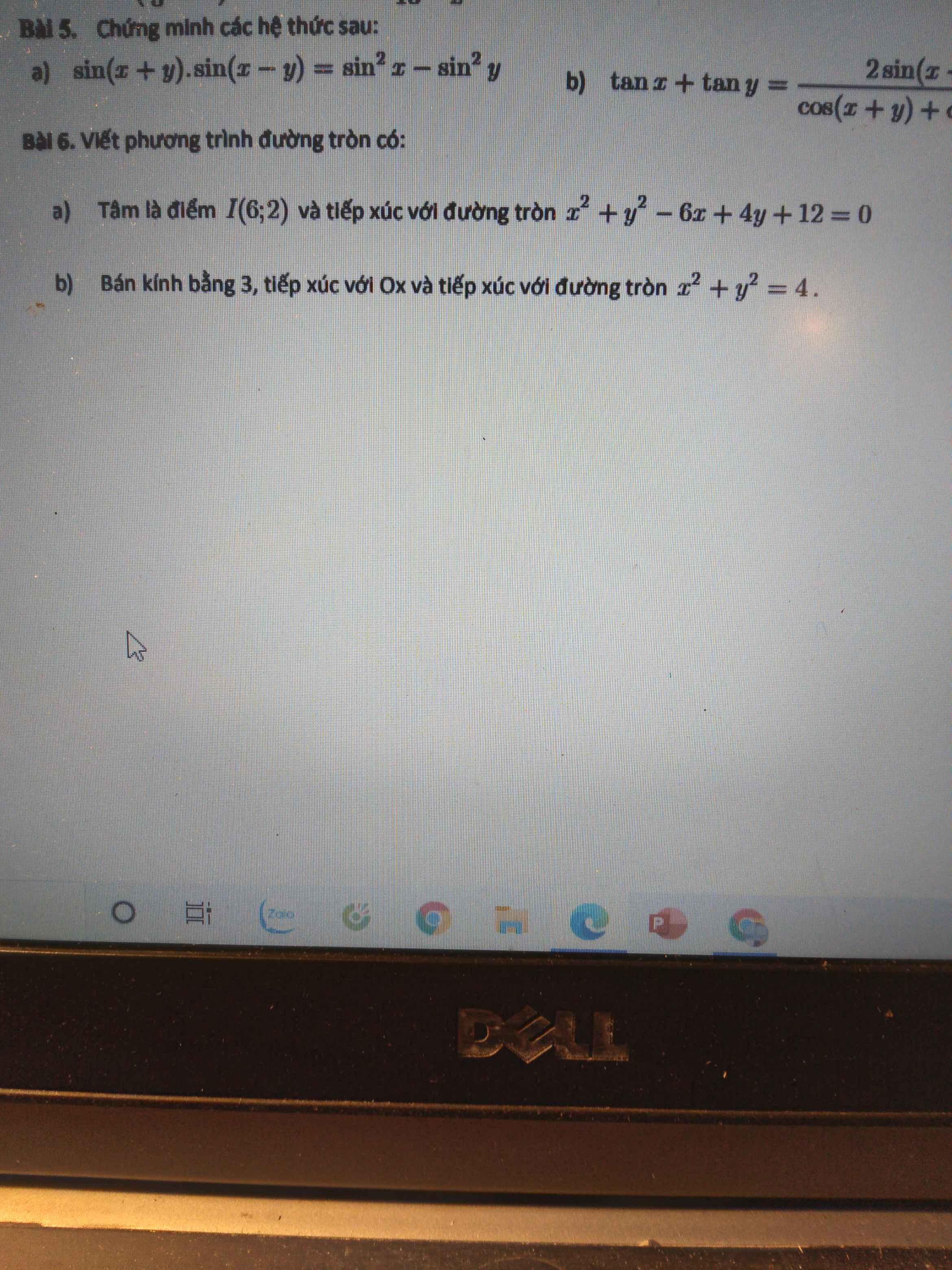
Đường tròn (C): \(x^2+y^2-6x+4y+12=0\) có tâm \(J\left(3;-2\right)\) bán kính \(r=1\)
Tiếp điểm A của 2 đường tròn phải nằm trên đường nối tâm IJ
\(\overrightarrow{JI}=\left(3;4\right)\Rightarrow\) phương trình IJ có dạng:
\(4\left(x-3\right)-3\left(y+2\right)=0\Leftrightarrow4x-3y-18=0\)
Tọa độ tiếp điểm A là nghiệm của hệ :
\(\left\{{}\begin{matrix}4x-3y-18=0\\x^2+y^2-6x+4y+12=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{4x-18}{3}\\x^2+y^2-6x+4y+12=0\end{matrix}\right.\)
\(\Rightarrow x^2+\left(\dfrac{4x-18}{3}\right)^2-6x+4\left(\dfrac{4x-18}{3}\right)+12=0\)
\(\Rightarrow\dfrac{25}{9}x^2-\dfrac{50}{3}x+24=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{12}{5}\Rightarrow y=-\dfrac{14}{5}\\x=\dfrac{18}{5}\Rightarrow y=-\dfrac{6}{5}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}A\left(\dfrac{12}{5};-\dfrac{14}{5}\right)\\A\left(\dfrac{18}{5};-\dfrac{6}{5}\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\overrightarrow{AI}=\left(\dfrac{18}{5};\dfrac{24}{5}\right)\\\overrightarrow{AI}=\left(\dfrac{12}{5};\dfrac{16}{5}\right)\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}R^2=AI^2=36\\R^2=AI^2=\dfrac{36}{5}\end{matrix}\right.\)
Có 2 đường tròn thỏa mãn:
\(\left[{}\begin{matrix}\left(x-6\right)^2+\left(y-2\right)^2=36\\\left(x-6\right)^2+\left(y-2\right)^2=\dfrac{36}{5}\end{matrix}\right.\)
b.
Đường tròn (C): \(x^2+y^2=4\) có tâm \(O\left(0;0\right)\) và bán kính \(r=2\)
Gọi \(I\left(a;b\right)\) là tâm của đường tròn (C') cần tìm
Do (C') tiếp xúc Ox \(\Rightarrow d\left(I;Ox\right)=3\Rightarrow\dfrac{\left|b\right|}{1}=3\Rightarrow b=\pm3\)
TH1: \(I\left(a;3\right)\Rightarrow\overrightarrow{OI}=\left(a;3\right)\Rightarrow OI=\sqrt{a^2+9}\)
Do 2 đường tròn tiếp xúc \(\Rightarrow\left[{}\begin{matrix}R+r=OI\\R-r=OI\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}OI=5\\OI=1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\sqrt{a^2+9}=5\\\sqrt{a^2+9}=1\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow a=\pm4\)
TH2: hoàn toàn tương tự ta có tìm được \(a=\pm4\)
Vậy có 4 đường tròn thỏa mãn: \(\left[{}\begin{matrix}\left(x-4\right)^2+\left(y-3\right)^2=9\\\left(x+4\right)^2+\left(y-3\right)^2=9\\\left(x-4\right)^2+\left(y+3\right)^2=9\\\left(x+4\right)^2+\left(y+3\right)^2=9\end{matrix}\right.\)