74,3.....+...........,......5 =90,24
xin nhờ các bạn giúp đỡ
Xin nhờ quý thầy cô và các bạn yêu toán gần xa giúp đỡ với ạ!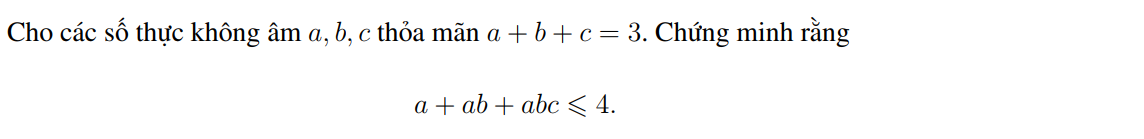
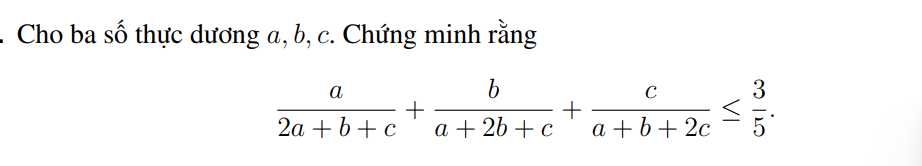
Áp dụng BĐT cosi dạng \(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\)
\(\Leftrightarrow\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\cdot\dfrac{1}{4}\ge\dfrac{4}{a+b}\cdot\dfrac{1}{4}\\ \Leftrightarrow\dfrac{1}{a+b}\le\dfrac{1}{4}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\)
\(\Leftrightarrow\dfrac{a}{2a+b+c}=\dfrac{a}{a+b+a+c}\le\dfrac{a}{4}\left(\dfrac{1}{a+b}+\dfrac{1}{a+c}\right)\)
Cmtt \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{b}{a+2b+c}\le\dfrac{b}{4}\left(\dfrac{1}{a+b}+\dfrac{1}{b+c}\right)\\\dfrac{c}{a+b+2c}\le\dfrac{c}{4}\left(\dfrac{1}{a+c}+\dfrac{1}{b+c}\right)\end{matrix}\right.\)
Cộng VTV 3 BĐT trên:
\(\Leftrightarrow VT\le\dfrac{1}{4}\left(\dfrac{a}{a+b}+\dfrac{a}{a+c}+\dfrac{b}{a+b}+\dfrac{b}{b+c}+\dfrac{c}{a+c}+\dfrac{c}{b+c}\right)\\ \Leftrightarrow VT\le\dfrac{1}{4}\left(\dfrac{a+b}{a+b}+\dfrac{b+c}{b+c}+\dfrac{a+c}{a+c}\right)=\dfrac{1}{4}\cdot3=\dfrac{3}{4}\)
Dấu \("="\Leftrightarrow a=b=c\)
Em xin phép nhờ thầy cô và các bạn giúp đỡ với ạ, em cám ơn nhiều
Xin phép nhờ quý thầy cô và các bạn giúp đỡ với ạ. Em cám ơn nhiều
Em xin phép được nhờ quý thầy cô và các bạn giúp đỡ!
Em cám ơn nhiều lắm ạ!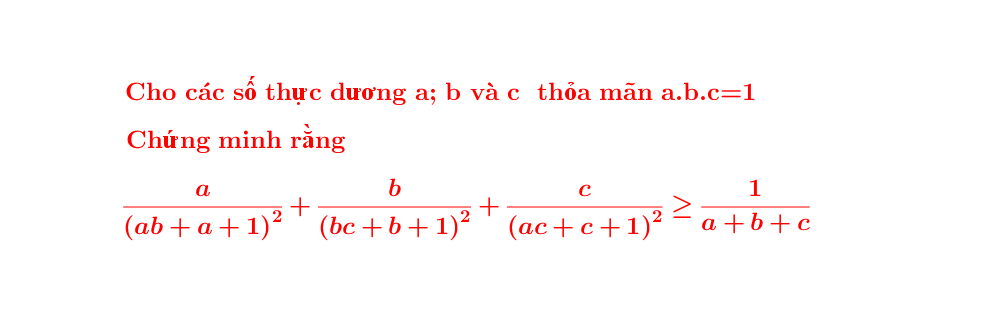
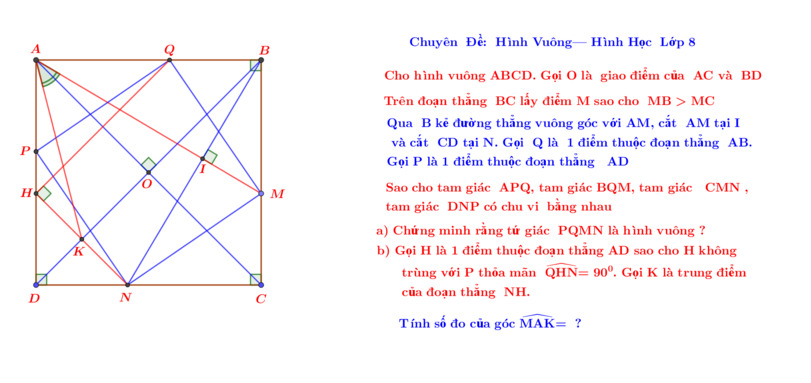
Em xin phép nhờ quý thầy cô và các bạn giúp đỡ với ạ, em cám ơn nhiều ạ
-Để mình suy nghĩ ngồi làm cho bạn nhé.
-Vì bài dài quá nên mình nói tóm tắt:
a) -Bạn chứng minh △ABM = △BCN (g-c-g) do có \(AB=BC\) , \(\widehat{BCN}=\widehat{ABM}=90^0\),\(\widehat{NBC}=\widehat{MAB}\) (bạn tự chứng minh).
-Suy ra: \(BM=CN\) .
-Suy ra 2 điều:
+\(QM^2-BQ^2=MN^2-MC^2\)
+\(QM+BQ=MN+MC\) (1)
\(QM^2-BQ^2=MN^2-MC^2\)
\(\Rightarrow\left(QM-BQ\right)\left(QM+BQ\right)=\left(MN-MC\right)\left(MN+MC\right)\)
\(\Rightarrow QM-BQ=MN-MC\) (2)
-Từ (1),(2) suy ra \(QM=MN\) nên △BMQ=△CNM (ch-cgv).
\(\Rightarrow\) MQ vuông góc với MN (bạn tự c/m).
\(QM=MN\) nên \(BQ=MC\) nên \(AQ=BM\Rightarrow PQ^2-AP^2=QM^2-BQ^2;QM+BQ=PQ+AP\)
Nên \(PQ=QM;\Delta APQ=\Delta BQM\) nên PQ⊥QM ; AP=BQ nên PQ=AQ
-Từ PQ=AQ bạn tự c/m PN=PQ (theo sườn mình đã cho) rồi sau đó c/m tam giác APQ=tam giác DNP rồi từ đó suy ra PQ vuông góc PN
.......
Xin phép được nhờ quý thầy cô giáo và các bạn giúp đỡ em bài toán nâng cao lớp 8 học kỳ 1.
#đường_trung_bình_của_tam_giác.
Tìm tất cả các số nguyên tố \(p;q;r\) thỏa mãn \(5.p^4-6.q^4+7.r^2=-1322\)
P/s: em xin phép nhờ quý thầy cô giáo và các bạn yêu toán gợi ý, giúp đỡ em tham khảo với ạ!
Tìm tất cả các cặp số nguyên tố \(\left(p,q\right)\) thỏa mãn : \(p^q+7.q^p\) cũng là số nguyên tố ?
P/s: Em xin phép nhờ sự giúp đỡ của quý thầy cô giáo và các bạn yêu toán, gợi ý giúp đỡ
em với ạ !
Em cám ơn nhiều ạ!
Đặt \(a=p^q+7q^p\)
Nếu p; q đều bằng 2 \(\Rightarrow a=2^2+7.2^2\) là hợp số (ktm)
Nếu p; q cùng lớn hơn 2 \(\Rightarrow p^q\) và \(q^p\) đều lẻ
\(\Rightarrow a=p^q+7q^p\) là số chẵn lớn hơn 2 \(\Rightarrow\) là hợp số (ktm)
\(\Rightarrow\) Có đúng 1 số trong p; q phải bằng 2, số còn lại là SNT lẻ
TH1: \(p=2\Rightarrow a=2^q+7.q^2\)
- Nếu \(q=3\Rightarrow a=2^3+7.3^2=71\) là SNT (thỏa mãn)
- Nếu \(q>3\Rightarrow q^2\equiv1\left(mod3\right)\Rightarrow7q^2\equiv1\left(mod3\right)\)
\(2^q=2^{2k+1}=2.4^k\equiv2\left(mod3\right)\)
\(\Rightarrow a=2^q+7.q^2\equiv2+1\left(mod3\right)\Rightarrow a⋮3\) là hợp số (ktm)
TH2: \(q=2\Rightarrow a=p^2+7.2^p\)
- Nếu \(p=3\Rightarrow a=3^2+7.2^3=65\) ko phải SNT (ktm)
- Nếu \(p>3\Rightarrow p^2\equiv1\left(mod3\right)\)
\(7.2^p=7.2^{2k+1}=14.4^k\equiv2\left(mod3\right)\)
\(\Rightarrow p^2+7.2^p⋮3\) là hợp số (ktm)
Vậy \(\left(p;q\right)=\left(2;3\right)\) là cặp SNT duy nhất thỏa mãn yêu cầu
Có tồn tại hay không các số nguyên \(a\) và \(b\) sao cho \(2a^5.b+3\) và \(32a.b^5+3\) là các số lập phương ?
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán gợi ý , giúp đỡ em tham khảo với ạ!
Em cám ơn nhiều lắm ạ!