cho tam giác ABC cân tại A. \(\widehat{BAC}\)=120\(^0\), AB=a. tính độ dài cạnh BC theo a

Những câu hỏi liên quan
Cho tam giác ABC cân tại A có góc A = 120 độ , AB = 6cm. Tính độ dài cạnh BC
Cho tam giác ABC cân tại A có AB<BC.Trên cạnh BC lấy hai điểm M và N sao cho BM=CN=AB.
a)Chứng minh rằng tam giác AMN cân.
b)Tính các góc của tam giác AMN khi góc BAC=120 độ.
Xét tam gia ABM va ANC co:
AB = AC(gt)
\(\widehat{B}\) =\(\widehat{C}\) (gt)
BM =NC (gt)
=> \(\Delta\) ABM =\(\Delta\) ANC (C.G.C)
Đúng 0
Bình luận (0)
Cho tam giác cân ABC cân tại A. Tia phân giác của góc BAC cắt cạnh BCtại M.1) Chứng minh tam giác AMB tam giác AMC.2) a- Biết góc BAC 500. Tính góc ABC và góc ACB.b- Biết BC 6 cm; AM 4 cm. Tính độ dài AB, AC?3) Kẻ ME vuông góc AB tại E, MF vuông góc AC tại F. Chứng minh tam giác AEF cân.4) Kẻ EI vuông góc BC tại I. Gọi K là giao của đường thẳng EI và đường thẳng AC. Chứngminh A là trung điểm của đoạn KF.
Đọc tiếp
Cho tam giác cân ABC cân tại A. Tia phân giác của góc BAC cắt cạnh BC
tại M.
1) Chứng minh tam giác AMB = tam giác AMC.
2) a- Biết góc BAC = 500. Tính góc ABC và góc ACB.
b- Biết BC = 6 cm; AM = 4 cm. Tính độ dài AB, AC?
3) Kẻ ME vuông góc AB tại E, MF vuông góc AC tại F. Chứng minh tam giác AEF cân.
4) Kẻ EI vuông góc BC tại I. Gọi K là giao của đường thẳng EI và đường thẳng AC. Chứng
minh A là trung điểm của đoạn KF.
1: Xét ΔAMB và ΔAMC có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó:ΔAMB=ΔAMC
2:
a: \(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-50^0}{2}=65^0\)
b: BC=6cm nên BM=3cm
=>AB=AC=5cm
3: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
Suy ra: AE=AF
hay ΔAEF cân tại A
Đúng 2
Bình luận (1)
Cho tam giác ABC có \(AB = 5,BC = 7,\widehat A = {120^o}.\) Tính độ dài cạnh AC.
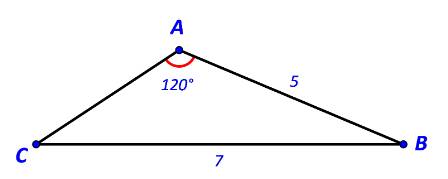
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}}\)
\( \Rightarrow \sin C = \sin A.\frac{{AB}}{{BC}} = \sin {120^o}.\frac{5}{7} = \frac{{5\sqrt 3 }}{{14}}\)
\( \Rightarrow \widehat C \approx 38,{2^o}\) hoặc \(\widehat C \approx 141,{8^o}\) (Loại)
Ta có: \(\widehat A = {120^o},\widehat C = 38,{2^o}\)\( \Rightarrow \widehat B = {180^o} - \left( {{{120}^o} + 38,{2^o}} \right) = 21,{8^o}\)
Áp dụng định lí cosin trong tam giác ABC ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {5^2} + {7^2} - 2.5.7.\cos 21,{8^o}\\ \Rightarrow A{C^2} \approx 9\\ \Rightarrow AC = 3\end{array}\)
Vậy độ dài cạnh AC là 3.
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, AB > BC. Tia phân giác của BAC cắt cạnh BC tại H.
a) Chứng minh: AH ⊥ BC.
b) Tính độ dài AH nếu BC = 8cm, AB = 10cm.
c) Tia phân giác của góc ABC cắt AH tại I. Chứng minh tam giác BIC cân.
d) Đường thẳng đi qua A và song song với BC cắt tia BI, CI lần lượt tại M và N.
Chứng minh A là trung điểm của đoạn thẳng MN.
a: ta có: ΔABC cân tại A
mà AH là đường phân giác
nên AH vừa là đường cao vừa là đừog trung tuyến
b: Vì H là trung điểm của BC
nên BH=CH=4cm
\(AH=\sqrt{AB^2-AH^2}=2\sqrt{21}\left(cm\right)\)
c: Xét ΔBIC có
IH là đường cao
IH là đường trung tuyến
Do đó:ΔBIC cân tại I
Đúng 0
Bình luận (0)
Cho tam giác ABC có \(AB = 3,AC = 4,\widehat {BAC} = {120^o}.\) Tính (làm tròn kết quả đến hàng đơn vị):
a) Độ dài cạnh BC và độ lớn góc B.
b) Bán kính đường tròn ngoại tiếp
c) Diện tích của tam giác
d) Độ dài đường cao xuất phát từ A
e) \(\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AM} .\overrightarrow {BC} \) với M là trung điểm của BC.
a) Áp dụng định lí cosin trong tam giác ABC, ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\\ \Leftrightarrow B{C^2} = {3^2} + {4^2} - 2.3.4.\cos {120^o}\\ \Leftrightarrow B{C^2} = 37\\ \Leftrightarrow BC \approx 6\end{array}\)
Áp dụng định lí sin trong tam giác ABC, ta có:
\(\begin{array}{l}\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = 2R\\ \Rightarrow \sin B = \frac{{AC.\sin A}}{{BC}} = \frac{{4.\sin {{120}^o}}}{6} = \frac{{\sqrt 3 }}{3}\\ \Leftrightarrow \widehat B \approx {35^o}\end{array}\)
b) \(R = \frac{{BC}}{{2.\sin A}} = \frac{6}{{2.\sin {{120}^o}}} = 2\sqrt 3 \)
c) Diện tích tam giác ABC: \(S = \frac{1}{2}4.3.\sin {120^o} = 3\sqrt 3 .\)
d) Gọi H là chân đường cao hạ từ đỉnh A.
Ta có: \(S = \frac{1}{2}AH.BC\)
\( \Rightarrow AH = \frac{{2S}}{{BC}} = \frac{{2.3\sqrt 3 }}{6} = \sqrt 3 \)
e) \(\overrightarrow {AB} .\overrightarrow {AC} = 3.4.\cos (\widehat {BAC}) = 12.\cos {120^o} = - 6.\)
Ta có: \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \) (do M là trung điểm BC)
\( \Leftrightarrow \overrightarrow {AM} = \frac{1}{2}(\overrightarrow {AB} + \overrightarrow {AC} )\)
\(\begin{array}{l} \Rightarrow \overrightarrow {AM} .\overrightarrow {BC} = \frac{1}{2}(\overrightarrow {AB} + \overrightarrow {AC} )(\overrightarrow {AC} - \overrightarrow {AB} )\\ = \frac{1}{2}\left( {{{\overrightarrow {AC} }^2} - {{\overrightarrow {AB} }^2}} \right) = \frac{1}{2}\left( {A{C^2} - A{B^2}} \right)\\ = \frac{1}{2}\left( {{4^2} - {3^2}} \right) = \frac{7}{2}.\end{array}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có cạnh đáy bằng 14cm. kẻ tia phân giác AD của góc BAC (D thuộc BC). Tính độ dài cạng AB biết AD = 15cm
Cho tam giác ABC cân tại A có cạnh đáy bằng 14cm kẻ tia phân giác AD của góc BAC (D thuộc BC). Tính độ dài cạnh AB biết
AD = 15cm .
Cho tam giác ABC cân tại A nội tiếp trong đường tròn (O;R) có AB = R.
a, CMR: AO là tia phân giác của góc BAC
b, C/tỏ BC > R. So sánh khoảng cách từ tâm O đến các cạnh của tam giác ABC.
c, Tính theo R độ dài cạnh BC và chiều cao AH hạ từ A đến BC















