Giúp mình câu 4 với ạ,mình cảm ơn nhiềuu

Những câu hỏi liên quan
Mn ơi giải giúp mình câu 6.4, 6.5 và 7.1 va ạ. Mình cảm ơn nhiềuu
6.4
\(y=\dfrac{3}{2}\left(1+cos2x\right)-\sqrt{3}sin2x+\dfrac{1}{2}-\dfrac{1}{2}cos2x\)
\(=cos2x-\sqrt{3}sin2x+2\)
\(=2\left(\dfrac{1}{2}cos2x-\dfrac{\sqrt{3}}{2}sin2x\right)+2\)
\(=2cos\left(2x-\dfrac{\pi}{3}\right)+2\)
Do \(-1\le cos\left(2x-\dfrac{\pi}{3}\right)\le1\)
\(\Rightarrow0\le y\le4\)
\(y_{min}=0\) khi \(cos\left(2x-\dfrac{\pi}{3}\right)=-1\)
\(y_{max}=4\) khi \(cos\left(2x-\dfrac{\pi}{3}\right)=1\)
Đúng 1
Bình luận (1)
6.5
Ủa nhìn bài 7 thì đây là chương trình lớp 11 (pt lượng giác) chứ đâu phải lớp 10?
Vậy giải theo kiểu lớp 11 nghe:
\(y=\dfrac{2+cosx+3sinx}{2+cosx}\)
\(\Leftrightarrow2y+y.cosx=2+cosx+3sinx\)
\(\Leftrightarrow3sinx+\left(1-y\right).cosx=2y-2\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(9+\left(1-y\right)^2\ge\left(2y-2\right)^2\)
\(\Leftrightarrow\left(y-1\right)^2\le3\)
\(\Rightarrow1-\sqrt{3}\le y\le1+\sqrt{3}\)
Đúng 1
Bình luận (0)
7.
\(\Leftrightarrow\left(m+1\right)\left[\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)\right]+cos4x=0\)
\(\Leftrightarrow\left(m+1\right)\left(1-3sin^2x.cos^2x\right)+cos4x=0\)
\(\Leftrightarrow\left(m+1\right)\left(1-\dfrac{3}{4}sin^22x\right)+cos4x=0\)
\(\Leftrightarrow\left(m+1\right)\left(1-\dfrac{3}{8}\left(1-cos4x\right)\right)+cos4x=0\)
\(\Leftrightarrow\left(m+1\right)\left(\dfrac{5}{8}+\dfrac{3}{8}cos4x\right)+cos4x=0\)
\(\Leftrightarrow5\left(m+1\right)+\left(3m+11\right)cos4x=0\)
\(\Leftrightarrow\left(3m+11\right)cos4x=-5\left(m+1\right)\)
- Với \(m=-\dfrac{11}{3}\) pt vô nghiệm
- Với \(m\ne-\dfrac{11}{3}\)
\(\Rightarrow cos4x=\dfrac{-5\left(5m+1\right)}{3m+11}\)
Do \(-1\le cos4x\le1\) nên pt có nghiệm khi:
\(-1\le\dfrac{-5\left(m+1\right)}{3m+11}\le1\)
Tới đây chắc bạn tự làm tiếp được đúng ko? Tách ra làm 2 BPT rồi sau đó giao nghiệm thôi
Đúng 1
Bình luận (1)
Giúp mình với ạ,cảm ơn nhiềuu 
Giúp mình với ạ, cho mình lời giải cho tiết với nhé. Cảm ơn các bạn nhiềuu 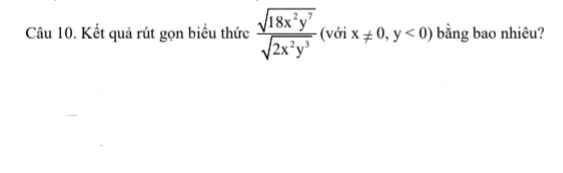


,MỌI NG ƠI GIÚP MÌNH 2 CÂU NÀY VỚI Ạ! MÌNH CẢM ƠN NHIỀUU
Cho tệp BAIKT.INP chứa các số nguyên bất kì. Viết chương trình đếm xem trong tệp có bao nhiêu số lẻ rồi ghi kết quả vào tệp KETQUA.OUT giúp mình với mình đang gấp ạ. Mình cảm ơn nhiềuu

giúp em với ạ em cảm ơn nhiềuu
\(\dfrac{n}{2n-1}>\dfrac{n}{2n}=\dfrac{1}{2}\)
\(\Rightarrow x_{n+1}>\dfrac{1}{2}.\left(\dfrac{x_n^2+2}{x_n}\right)\ge\dfrac{1}{2}.\dfrac{2\sqrt{2x_n^2}}{x_n}=\sqrt{2}\)
Dãy bị chặn dưới bởi \(\sqrt{2}\)
Ta sẽ chứng minh dãy đã cho là dãy giảm, hay \(x_{n+1}-x_n< 0\) với \(n>1\)
\(\Leftrightarrow\dfrac{n}{2n-1}\left(\dfrac{x_n^2+2}{x_n}\right)-x_n< 0\Leftrightarrow\left(1-n\right)x_n^2+2n< 0\)
\(\Leftrightarrow x_n^2>\dfrac{2n}{n-1}\Leftrightarrow x_n>\sqrt{\dfrac{2n}{n-1}}\)
Do \(x_n=\dfrac{n-1}{2\left(n-1\right)-1}.\left(\dfrac{x_{n-1}^2+2}{x_{n-1}}\right)=\dfrac{n-1}{2n-3}.\left(\dfrac{x_{n-1}^2+2}{x_{n-1}}\right)\ge\dfrac{2\sqrt{2}\left(n-1\right)}{2n-3}\)
Nên ta chỉ cần chứng minh: \(\dfrac{2\sqrt{2}\left(n-1\right)}{2n-3}>\sqrt{\dfrac{2n}{n-1}}\)
\(\Leftrightarrow6n-8>0\) (đúng)
Vậy dãy đã cho là dãy giảm
Dãy giảm và bị chặn dưới nên có giới hạn
Gọi giới hạn của dãy là L, lấy giới hạn 2 vế biểu thức truy hồi:
\(\lim\left(x_{n+1}\right)=\lim\left(\dfrac{n}{2n-1}.\dfrac{x_n^2+2}{x_n}\right)\Rightarrow L=\dfrac{1}{2}\left(\dfrac{L^2+2}{L}\right)\)
\(\Rightarrow L^2=2\Rightarrow L=\sqrt{2}\)
Đúng 1
Bình luận (2)
Cho 6,2g Na2O tại dung dịch H2O thu được 200ml dung dịch Bazơ. a) Tính nồng độ mol dd Bazơ? b) Trung hòa dd Bazơ trên bằng dd H2SO4 20%. Tính V dung dịch H2SO4.
Giúp mình với ạ, mình đang cần gấp. Mình cảm ơn mng rất nhiềuu
\(n_{Na_2O}=\dfrac{6,2}{62}=0,1 \left(mol\right)\)
\(2Na+2H_2O\rightarrow2NaOH+H_2\)
0,1 -----------------> 0,1
\(CM_{base}=CM_{NaOH}=\dfrac{0,1}{0,2}=0,5M\)
b
\(H_2SO_4+2NaOH\rightarrow Na_2SO_4+2H_2O\)
0,05 <------ 0,1
\(V_{H_2SO_4}=\dfrac{0,05}{0,2}=0,25\left(l\right)\Rightarrow V_{dd.H_2SO_4}=\dfrac{0,25.100}{20}=1,25\left(l\right)\)
Đúng 1
Bình luận (0)
Giúp em với ạ, em cảm ơn rất nhiềuu
a.
\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{4+x}-2}{4x}=\lim\limits_{x\rightarrow0}\dfrac{\left(\sqrt{4+x}-2\right)\left(\sqrt{4+x}+2\right)}{4x\left(\sqrt{4+x}+2\right)}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{x}{4x\left(\sqrt{4+x}+2\right)}=\lim\limits_{x\rightarrow0}\dfrac{1}{4\left(\sqrt{4+x}+2\right)}=\dfrac{1}{4\left(\sqrt{4+0}+2\right)}=\dfrac{1}{16}\)
b.
\(\lim\limits_{x\rightarrow1}\dfrac{\sqrt[3]{x+7}-2}{x-1}=\lim\limits_{x\rightarrow1}\dfrac{\left(\sqrt[3]{x+7}-2\right)\left(\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4\right)}{\left(x-1\right)\left(\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{x-1}{\left(x-1\right)\left(\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4\right)}=\lim\limits_{x\rightarrow1}\dfrac{1}{\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4}\)
\(=\dfrac{1}{\sqrt[3]{8^2}+2\sqrt[3]{8}+4}=\dfrac{1}{12}\)
Đúng 1
Bình luận (2)
giúp e với ạ e cảm ơn rất nhiềuu
Lời giải:
Gọi chiều dài và chiều rộng ban đầu là $a$ và $a-25$ (m)
Diện tích ban đầu: $a(a-25)$
Diện tích sau thay đổi: $(a-25)(a-25)$
Theo bài ra: $a(a-25)-(a-25)(a-25)=1000$
$\Leftrightarrow (a-25)[a-(a-25)]=1000$
$\Leftrightarrow 25(a-25)=1000$
$\Leftrightarrow a-25=40$
$\Leftrightarrow a=65$ (m)
Vậy mảnh đất ban đầu có chiều dài 65 m, chiều rộng 40 m
Đúng 0
Bình luận (0)
giúp mình câu 3d với câu 4 với ạ ghi chi tiết giúp mình cảm ơn anh chị nhiều
3d:
20<x<45
x chia 4 dư 1 nên x-1 thuộc B(4)
=>\(x-1\in\left\{0;4;...;44;48\right\}\)
=>\(x\in\left\{1;5;...;45;49\right\}\)
mà 20<x<45
nên x thuộc {21;26;31;35;41}
4:
a: A={x∈N|51<=x<=127}
b: B={x∈N|100<=x<=999}
c: C={x∈N|x=7k+5; 0<=k<=8}
Đúng 0
Bình luận (0)




















