tìm m
(m+4)\(^2\)-12>0
Tìm m để phương trình có 4 nghiệm:
\(x^4-6x^3+5x^2+\left(2m+12\right)x-m^2-3m=0\)
\(\Leftrightarrow x^4-2x^3-\left(m+3\right)x^2-4x^3+8x^2+4\left(m+3\right)x+mx^2-2mx-m^2-3m=0\)
\(\Leftrightarrow x^2\left(x^2-2x-m-3\right)-4x\left(x^2-2x-m-3\right)+m\left(x^2-2x-m-3\right)=0\)
\(\Leftrightarrow\left(x^2-4x+m\right)\left(x^2-2x-m-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-4x+m=0\\x^2-2x-m-3=0\end{matrix}\right.\)
Pt có 4 nghiệm khi: \(\left\{{}\begin{matrix}\Delta'_1=4-m\ge0\\\Delta'_2=1+m+3\ge0\end{matrix}\right.\)
\(\Leftrightarrow-4\le m\le4\)
Cho phương trình x2+4(m-1)x-12=0. Tìm m sao cho 4|x1-2|\(\sqrt{4-mx_2}\)=(x1+x2-x1x2-8)2
Cho phương trình (2m - 1) x 2 - 2(m + 4)x + 5m + 2 = 0 ( m ≠ 1 2 )
Tìm giá trị của m để phương trình có nghiệm.
cho phương trình mx^2 + 12 x − 4 = 0
a,giải phương trình với m=1
b,tìm m để phương trình có 2 nghiệm phân biệt
c,tìm m để phương trình có 2 nghiệm kép tìm nghiệm kép đó
d,tìm m để phương trình vô nghiệm
a) Thay \(m=1\) vào phương trình, ta được:
\(x^2+12x-4=0\) \(\Rightarrow\left[{}\begin{matrix}x=-6+2\sqrt{10}\\x=-6-2\sqrt{10}\end{matrix}\right.\)
Vậy ...
b)
+) Với \(m=0\) \(\Rightarrow12x-4=0\) \(\Leftrightarrow x=\dfrac{1}{3}\)
+) Với \(m\ne0\), ta có: \(\Delta'=36+4m\)
Để phương trình có 2 nghiệm phân biệt \(\Leftrightarrow\Delta'>0\) \(\Leftrightarrow m>-9\)
Vậy \(\left\{{}\begin{matrix}m\ne0\\m>-9\end{matrix}\right.\) thì phương trình có 2 nghiệm phân biệt
c) Để phương trình có nghiệm kép \(\Leftrightarrow\Delta'=0\) \(\Leftrightarrow m=-9\)
\(\Rightarrow-9x^2+12x-4=0\) \(\Leftrightarrow x=\dfrac{2}{3}\)
Vậy \(m=-9\) thì phương trình có nghiệm kép \(x_1=x_2=\dfrac{2}{3}\)
d) Để phương trình vô nghiệm \(\Leftrightarrow\Delta'< 0\) \(\Leftrightarrow m< -9\)
Vậy \(m< -9\) thì phương trình vô nghiệm
Tìm các giá trị của tham số m để bất phương trình sau luôn đúng: \(\dfrac{4x^2+4\left(m-2\right)x+22-m}{x^2+x+12}>0\)
Cho phương trình $x^{2}-2(m+1) x-4 m-12=0$ (ẩn $x$ ). Tìm $m$ để phương trình có hai nghiệm phân biệt $x_{1}, x_{2}$ sao cho $x_{1}-x_{2}=4$.
Để pt có 2 nghiệm pb khi \(\Delta>0\)
\(\Delta=\left(2m+2\right)^2-4\left(-4m-12\right)=4m^2+8m+4+16m+48\)
\(=4m^2+24m+52=4m^2+2.2m.6+36+16=\left(2m+6\right)^2+16>0\)
Vậy ta có đpcm
Theo Vi et \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=2m+2\\x_1x_2=\frac{c}{a}=-4m-12\end{cases}}\)
Ta có : \(x_1-x_2=4\Leftrightarrow\left(x_1-x_2\right)^2=16\Leftrightarrow x_1^2+x_2^2-2x_1x_2=16\)(*)
mà \(\left(x_1+x_2\right)^2=4m^2+8m+4\Rightarrow x_1^2+x_2^2=4m^2+8m+4-2\left(-4m-12\right)\)
\(=4m^2+16m+28\)
Thay vào (*) ta được : \(4m^2+16m+28-2\left(-4m-12\right)=16\)
\(\Leftrightarrow4m^2+24m+52=0\Leftrightarrow m=-3\pm2i\)
Cho phương trình (2m - 1) x 2 - 2(m + 4)x + 5m + 2 = 0 ( m ≠ 1 2 )
Tìm hệ thức giữa S và P sao cho trong hệ thức này không có m.
Phương trình (2m - 1) x 2 - 2(m + 4)x + 5m + 2 = 0 ( m ≠ 1 2 )
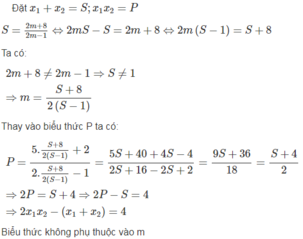
Bài 2. Cho biểu thức \(P=1+\frac{x-3}{x^2+5x+6}\left(\frac{8x^2}{4x^3-8x^2}-\frac{3x}{3x^2-12}-\frac{1}{x+2}\right)\).
a) Rút gọn P.
b) Tìm x để P = 0
c) Tìm x để P = 1
d) Tìm x để P > 0
Bài 3: Tìm m để các phương trình sau là phương trình bậc nhất ẩn x
a) (m - 4)x + 2 – m = 0
b) (m2 – 4) x – m =0
c) \(\frac{m-2}{m-1}x+5=0\)
d) \(\left(m+1\right)x^2+x-1=0\)
ĐKXĐ:\(x\ne\pm2;x\ne-3;x\ne0\)
\(P=1+\frac{x-3}{x^2+5x+6}\left(\frac{8x^2}{4x^3-8x^2}-\frac{3x}{3x^2-12}-\frac{1}{x+2}\right)\)
\(=1+\frac{x-3}{\left(x+2\right)\left(x+3\right)}\left[\frac{8x^2}{4x^2\left(x-2\right)}-\frac{3x}{3\left(x^2-4\right)}-\frac{1}{x+2}\right]\)
\(=1+\frac{x-3}{\left(x+2\right)\left(x+3\right)}\left(\frac{2}{x-2}-\frac{x}{x^2-4}-\frac{1}{x+2}\right)\)
\(=1+\frac{x-3}{\left(x+2\right)\left(x+3\right)}\left[\frac{2\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}-\frac{x}{\left(x-2\right)\left(x+2\right)}-\frac{x-2}{\left(x-2\right)\left(x+2\right)}\right]\)
\(=1+\frac{x-3}{\left(x+2\right)\left(x+3\right)}\cdot\frac{2x+4-x-x+4}{\left(x-2\right)\left(x+2\right)}\)
\(=1+\frac{8\left(x-3\right)}{\left(x+2\right)^2\left(x+3\right)\left(x-2\right)}\)
Đề sai à ??
Bài 1 : Cho biểu thức : \(P=1+\frac{x+3}{x^2+5x+6}\left(\frac{8x^2}{4x^3-8x^2}-\frac{3x}{3x^2-12}-\frac{1}{x-2}\right)\)
.
a) Rút gọn P.
b) Tìm x để P = 0
c) Tìm x để P = 1
d) Tìm x để P > 0
Bài 2 : Tìm m để các phương trình sau là phương trình bậc nhất ẩn x
a) (m - 4)x + 2 – m = 0
b) (m2 – 4) x – m =0
c) \(\frac{m-2}{m-1}x+5=0\)
d) \(\left(m+1\right)x^2+x-1=0\)