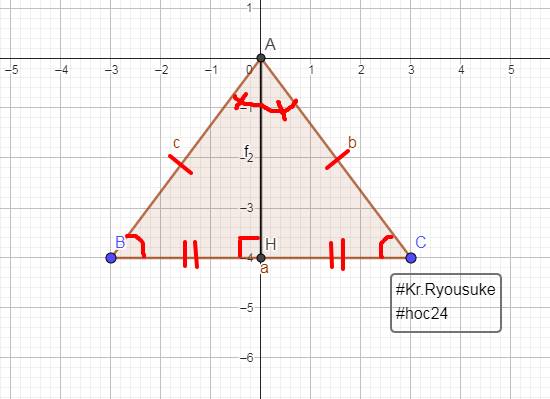
Cho tam giác ABC, đường cao AH, chứng minh rằng;
a) Nếu AB2 = BH.BC thì \(\widehat{BAC}\)=900
b) Nếu HA2 = BH.HC thì \(\widehat{BAC}\) =900
c) Nếu \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)và AH.BC = AB.AC thì \(\widehat{BAC}\) =900
C1. Cho tam giác nhọn DEF. Đường cao EA và FB cắt nhau tại H.
a) Chứng minh rằng
b) Chứng minh rằng
C2. Cho tam giác nhọn ABC. Đường cao BD và CE cắt nhau tại H.
a) Chứng minh rằng
b) Chứng minh rằng
C3. Cho ABC vuông tại A, đư¬ờng cao AH cắt đ¬ường phân giác CD tại I.
a) Chứng minh rằng:
b) Chứng minh AC2 = CH.BC
C4. Cho hình bình hành ABCD, trên cạnh AB lấy một điểm M. Đường thẳng DM cắt cạnh CB kéo dài tại N.
a) Chứng minh : MAD MBN
b) Chứng minh : MA.MN = MD.MB
cho tam giác ABC cân tại A , vẽ trung tuyến AH . chứng minh rằng AH cũng là phân giác , đường cao, đường trung tuyến của tam giác ABC
cho △ABC vuông tại A có AB = 3cm, BC = 5cm, vẽ đường cao AH của △ABC.
a) chứng minh tam giác ABC đồng dạng với tam giác HBA
b) chứng minh rằng AB2=BH.BC. Tính BH
c) dựng đường phân giác BD của tam giác ABC cắt AH ở E. Tính EH
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: ΔABC đồng dạng với ΔHBA
=>BA/BH=BC/BA
=>BA^2=BH*BC
BH=3^2/5=1,8cm
c: BE là phân giác
=>AE/AB=HE/BH
=>AE/5=HE/3=(AE+HE)/(5+3)=0,3
=>AE=1,5cm và HE=0,9cm
Cho tứ diện ABCD có tam giác ABC cân tại \(A\), tam giác BCD cân tại \(D\). Gọi I là trung điểm của cạnh BC.
a) Chứng minh rằng \(BC \bot (AID)\).
b) Kẻ đường cao AH của tam giác AID. Chứng minh rằng \(AH \bot (BCD)\).
c) Kẻ đường cao IJ của tam giác AID. Chứng minh rằng IJ là đường vuông góc chung của AD và BC.

a) Xét tam giác ABC cân tại A có
I là trung điểm của BC
\( \Rightarrow AI \bot BC\)
Xét tam giác ACD cân tại D có
I là trung điểm của BC
\( \Rightarrow DI \bot BC\)
Ta có \(AI \bot BC,DI \bot BC \Rightarrow BC \bot \left( {AID} \right)\)
b) \(BC \bot \left( {AID} \right);BC \subset \left( {BCD} \right) \Rightarrow \left( {BCD} \right) \bot \left( {AID} \right)\)
\(\left( {BCD} \right) \cap \left( {AID} \right) = DI\)
Trong (AID) có \(AH \bot DI\)
\( \Rightarrow AH \bot \left( {BCD} \right)\)
c) Ta có \(BC \bot \left( {AID} \right);IJ \subset \left( {AID} \right) \Rightarrow BC \bot IJ\)
Mà \(IJ \bot AD\)
Do đó IJ là đường vuông góc chung của AD và BC.
Cho tam giác ABC, đường cao AH. Chứng minh rằng đường thẳng BC là tiếp tuyến của đường tròn (A; AH).
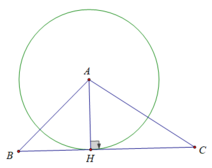
Ta có: BC đi qua điểm H thuộc đường tròn (A; AH)
BC ⊥ AH tại H
⇒ BC là tiếp tuyến của đường tròn (A; AH)
Cho tam giác ABC, đường cao AH. Chứng minh rằng đường thẳng BC là tiếp tuyến của đường tròn (A; AH).
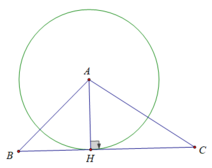
Ta có: BC đi qua điểm H thuộc đường tròn (A; AH)
BC ⊥ AH tại H
⇒ BC là tiếp tuyến của đường tròn (A; AH)
Cho tam giác ABC. Chứng minh rằng:
a) Nếu đường cao AH đồng thời là đường trung tuyến thì tam giác ABC cân tại A.
b) Nếu tam giác ABC cân tại A thì đường trung tuyến AH cũng là đường cao.
mình hong bik làm
1) Cho tam giác ABC vuông ở A và có đường cao AH,AB=5cm, AC=12cm
Tính độ dài các đoạn thẳng BC,AH
2)Cho tam giác ABC( góc A=90 độ), đường cao AH. chứng minh rằng AH2=BH.CH
Cho tam giác ABC vuông tại A, đường phân giác AD. Chứng minh rằng √2/AD = 1/AB + 1/AC. Kẻ đường cao AH và đường trung tuyến AM của tam giác ABC chứng minh rằng nếu 1/ah^2+1/am^2=2/ad^2. Giúp mình câu 2 thôi ạ mình cảm ơn
Để chứng minh rằng √2/AD = 1/AB + 1/AC, ta có thể sử dụng định lý phân giác trong tam giác vuông.
Vì tam giác ABC vuông tại A, nên ta có đường phân giác AD chia góc BAC thành hai góc bằng nhau.
Áp dụng định lý phân giác, ta có:
AB/BD = AC/CD
Từ đó, ta có:
AB/AD + AC/AD = AB/BD + AC/CD
= (AB + AC)/(BD + CD)
= (AB + AC)/BC
= 1/BC (vì tam giác ABC vuông tại A)
Vậy, ta có:
1/AD = 1/AB + 1/AC
√2/AD = √2/AB + √2/AC
Vậy, chứng minh đã được hoàn thành.
Để chứng minh rằng nếu 1/ah^2 + 1/am^2 = 2/ad^2, ta cần có thông tin chi tiết về tam giác ABC và các điều kiện đi kèm.
2/AD^2=(căn 2/AD)^2
=(1/AB+1/AC)^2
\(=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}+2\cdot\dfrac{1}{AB\cdot AC}\)
\(=\dfrac{1}{AH^2}+2\cdot\dfrac{1}{AH\cdot BC}\)
\(=\dfrac{1}{AH^2}+\dfrac{1}{AM^2}\)
Cho tam giác ABC cân tại A, đường cao AH
a, chứng minh: tam giác ABH = tam giác ACH
b, chứng minh: AH là đường phân giác của tam giác ABC
c, chứng minh: AH là đường trung trực của tam giác ABC
`a,`
Vì `\Delta ABC` cân tại A
`-> \text {AB = AC, }` $\widehat {B} = \widehat {C}$
Xét `\Delta ABH` và `\Delta ACH`:
`\text {AB = AC}`
$\widehat {B} = \widehat {C}$
$\widehat {AHB} = \widehat {AHC} (=90^0) (\text {AH là đường cao của} \Delta ABC)$
`=> \Delta ABH = \Delta ACH (ch-gn)`
`b,`
Vì `\Delta ABH = \Delta ACH (a)`
`->` $\widehat {BAH} = \widehat {CAH} (\text {2 cạnh tương ứng})$
`-> \text {AH là đường phân giác của}` `\Delta ABC`
`c,`
Vì `\Delta ABH = \Delta ACH (a)`
`-> \text {HB = HC}`
Ta có:
`\text {AH} \bot \text {BC}`
`\text {HB = HC}`
`-> \text {AH là đường trung trực của}` `\Delta ABC`.