Ta có: BC đi qua điểm H thuộc đường tròn (A; AH)
BC ⊥ AH tại H
⇒ BC là tiếp tuyến của đường tròn (A; AH)

Ta có: BC đi qua điểm H thuộc đường tròn (A; AH)
BC ⊥ AH tại H
⇒ BC là tiếp tuyến của đường tròn (A; AH)
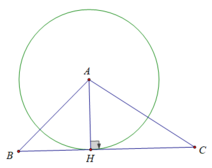
Cho tam giác ABC, đường cao AH. Chứng minh rằng đường thẳng BC là tiếp tuyến của đường tròn (A; AH).
Cho tam giác ABC có AB = 15 cm và AC= 8 cm và BC = 17 cm a) Chứng minh tam giác ABC vuôngb) Gọi AH là đường cao trong tam giác ABC, đường thẳng qua H vuông góc với AB cắt đường tròn (A;AH) tại D. Chứng minh BD là tiếp tuyến của đường tròn (A;AH)c) Tính HD.
Cho tam giác ABC vuông tại, đường cao AH. Vẽ đường tròn (A; AH). Kẻ các tiếp tuyến BD, CE với đường tròn (D, E là các tiếp điểm khác H). Chứng minh: a) BC là tiếp tuyến của đường tròn (A; AH) b) BD = BH; CE = CH c)BD+CE=BC d) Chứng minh ba điểm D, A, E thẳng hàng HẾT.
Cho tam giác abc có đường cao AH. Vẽ đường tròn tâm A, bán kính AH kẻ tiếp tuyến CD với đường tròn a) chứng minh BC là tiếp tuyến của ( A,AH) b) chứng minh AC lớn hơn hoặc bằng DH c) vẽ đường kính HK của (A,AH). Chứng minh DK//AC
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn (A;AH). Kẻ các tiếp tuyến BD, CE với đường tròn (D, E là các tiếp điểm khác H).
Chứng minh rằng:
DE tiếp xúc với đường tròn các đường kính BC
Cho tam giác ABC vuông tại A; đường cao AH. Vẽ đường tròn (A;AH). Gọi HD là đường kính của đường tròn đó. Tiếp tuyến của đường tròn tại D cắt CA ở E. Chứng minh rằng BE tiếp xúc với đường tròn (A) tại 1 điểm gọi là I và IA là tiếp tuyến của đường tròn đường kính BC
Cho tam giác ABC vuông tại A có AH là đường cao. Gọi BD, CE là các tiếp tuyến của đường tròn (A; AH) với D, E là các tiếp diêm. Chứng minh:
a, Ba điểm D, A, E thẳng hàng
b, DE tiếp xúc với đường tròn đường kính BC
Cho tam giác ABC. Hai đường cao BE, CF cắt nhau tại H. Gọi M và O lần lượt là trung điểm của AH, BC. Chứng minh rằng
a, AFHE là tứ giác nội tiếp
b, OE là tiếp tuyến của đường tròn đường kính AH
c, OE cắt AH tại S. Chứng minh rằng SE2=SH.SA
Cho tam giác ABC vuông tại A, có AB = 3cm, AC = 4cm. Đường cao AH. Vẽ đường tròn tâm A, bán kinh AH, kẻ các tiếp tuyến BD, CE với đường tròn tâm A (D. E là các tiếp điểm khác H). a) Tinh BC. AH. b) Chứng minh rằng : Ba điểm D. A. E thẳng hàng.