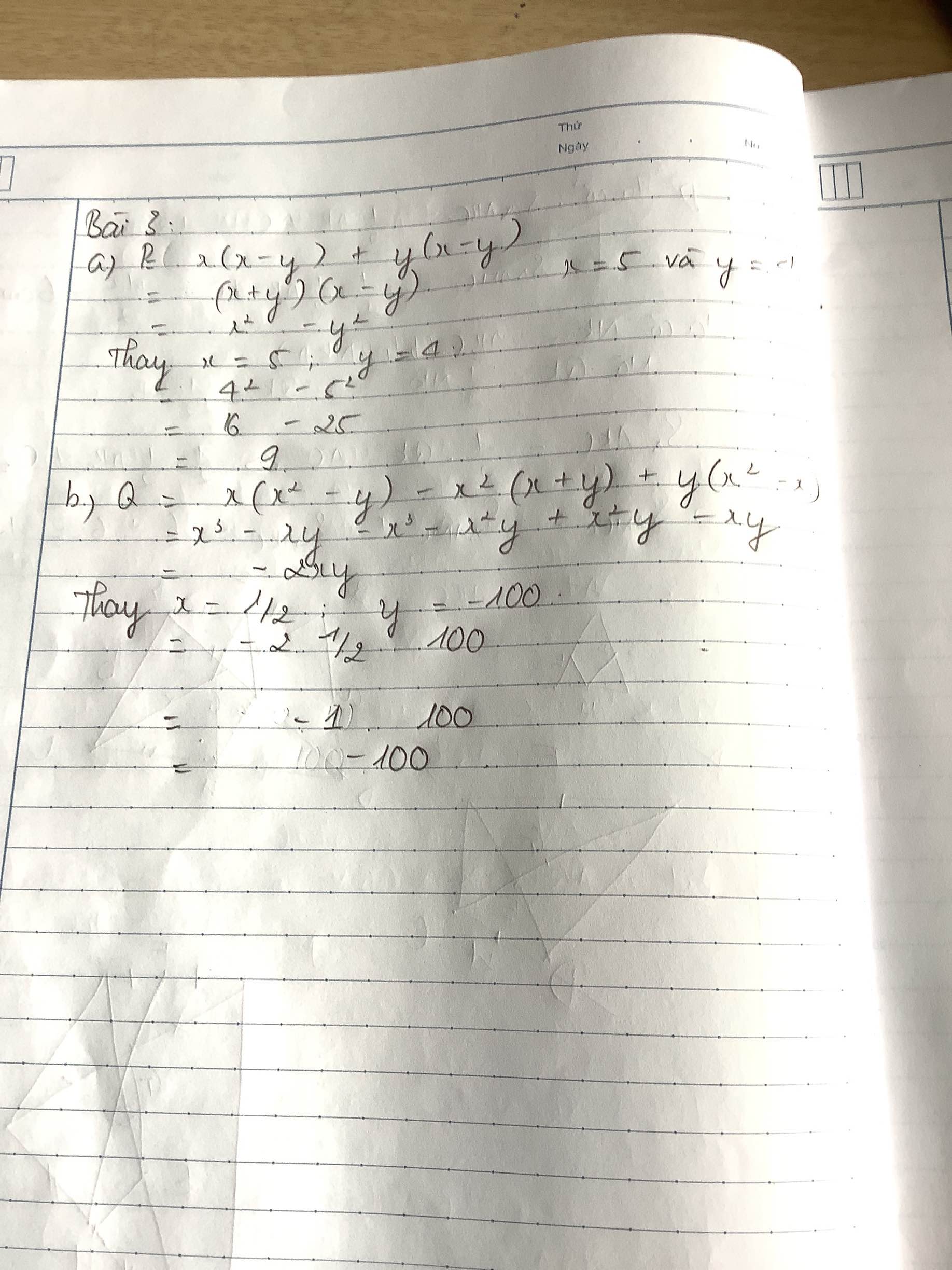tính giá trị của a và b tại x= -1

Những câu hỏi liên quan
a) Rút gọn A và tìm điều kiện của x để giá trị của A được xác định. b) Tính giá trị của A tại x = -2. c) Tính giá trị của x để giá trị của A = 4. d) Tính giá trị của x để giá trị của A = 1
a) ĐKXĐ: x≠ \(\dfrac{1}{2}\); x≠ \(\dfrac{-1}{2}\); x≠0
A= \(\left(\dfrac{1}{2x-1}+\dfrac{3}{1-4x^2}-\dfrac{2}{2x+1}\right):\dfrac{x^2}{2x^2+x}\)
= \(\left(\dfrac{2x+1-3-2\left(2x-1\right)}{4x^2-1}\right):\dfrac{x^2}{2x^2+x}\)
= \(\left(\dfrac{2x+1-3-4x+2}{4x^2-1}\right):\dfrac{x^2}{2x^2+x}\)
= \(\dfrac{-4x}{\left(2x+1\right)\left(2x-1\right)}.\dfrac{x\left(2x+1\right)}{x^2}\)
= \(\dfrac{-4x^2}{x^2\left(2x-1\right)}\)
= \(\dfrac{-4}{2x-1}\)
b) Tại x= -2 ta có A= \(\dfrac{-4}{2.\left(-2\right)-1}\)= \(\dfrac{4}{5}\)
c) A= 4 ta có \(\dfrac{-4}{2x-1}\)=4
⇔ -4 = 4(2x-1)
⇔ -4 = 8x-4
⇔ x = 0
d) A=1 ta có \(\dfrac{-4}{2x-1}\)=1
⇔ -4 = 2x-1
⇔ x= \(\dfrac{-3}{2}\)
Đúng 1
Bình luận (0)
Cho các đa thức : A = x^2 – 2x – y^2 + 3y – 1
B = - 2x^2 + 3y^2 – 5x + y + 3
a. Tính A + B và tính giá trị của đa thức A + B tại x = 2 và y = - 1 ?
b. Tính A – B và tính giá trị của đa thức A – B tại x = -2 và y = 1 ?
a. \(A+B=x^2-2x-y^2+3y-1-2x^2+3y^2-5x+y+3\)
\(=\left(x^2-2x^2\right)-\left(2x+5x\right)+\left(3y^2-y^2\right)+\left(3y+y\right)+\left(3-1\right)\)
\(=2y^2+4y-x^2-7x+2\)
Thay `x = 2` và `y = -1` vào `A + B` ta được:
\(2.\left(-1\right)^2+4.\left(-1\right)-2^2-7.2+2=-18\)
b. \(A-B=x^2-2x-y^2+3y-1-\left(-2x^2+3y^2-5x+y+3\right)\)
\(=x^2-2x-y^2+3y-1+2x^2-3y^2+5x-y-3\)
\(=\left(x^2+2x^2\right)+\left(5x-2x\right)-\left(y^2+3y^2\right)+\left(3y-y\right)-\left(1+3\right)\)
\(=3x^2+3x-4y^2+2y-4\)
Thay `x = -2` và `y = 1` vào `A - B` ta được:
\(3.\left(-2\right)^2+3.\left(-2\right)-4.1^2+2.1^2-4=0\)
Đúng 2
Bình luận (0)
Bài 3:
a, Tính giá trị của biểu thức A = \(5xy-10+3y\) tại \(x=2\) và \(y=-3\)
b, Tính giá trị của biểu thức B = \(8xy^2-xy-2x-10\) tại \(x=1\) và \(y=-1\)
a: \(A=5\cdot2\cdot\left(-3\right)-10+3\cdot\left(-3\right)=-30-10-9=-49\)
b: \(B=8\cdot1\cdot\left(-1\right)^2-1\cdot\left(-1\right)-2\cdot1-10\)
=8+1-2-10
=-3
Đúng 4
Bình luận (0)
a: A=5⋅2⋅(−3)−10+3⋅(−3)=−30−10−9=−49
b: B=8⋅1⋅(−1)2−1⋅(−1)−2⋅1−10
=8+1-2-10
=-3
Đúng 0
Bình luận (0)
a) tính giá trị của biểu thức: x^2+2y tại x=2, y= –3 b) tính giá trị của biểu thức: x^2+2xy+y^2 tại x=4, y=6 c) tính giá trị của biểu thức: P= x^2-4xy+4y^2 tại x=1 và y= 1/2
a: Khi x=2 và y=-3 thì \(x^2+2y=2^2+2\cdot\left(-3\right)=4-6=-2\)
b: \(A=x^2+2xy+y^2=\left(x+y\right)^2\)
Khi x=4 và y=6 thì \(A=\left(4+6\right)^2=10^2=100\)
c: \(P=x^2-4xy+4y^2=\left(x-2y\right)^2\)
Khi x=1 và y=1/2 thì \(P=\left(1-2\cdot\dfrac{1}{2}\right)^2=\left(1-1\right)^2=0\)
Đúng 3
Bình luận (0)
Cho biểu thức A = \(\dfrac{x+1}{2x+3}\) và biểu thức B = \(\dfrac{2x+3}{x+1}+\dfrac{x+2}{x+3}\)
a. Tìm điều kiện xác định của A và B
b. Tính giá trị của A tại x = -1 và giá trị của B tại x = -\(\dfrac{2}{3}\)
\(a,ĐK\left(A\right):x\ne-\dfrac{3}{2};ĐK\left(B\right):x\ne-1;x\ne-3\\ b,A=\dfrac{-1+1}{2\left(-1\right)+3}=0\\ B=\dfrac{2\left(-\dfrac{2}{3}\right)+3}{1-\dfrac{2}{3}}+\dfrac{2-\dfrac{2}{3}}{3-\dfrac{2}{3}}=\dfrac{3-\dfrac{4}{3}}{\dfrac{1}{3}}+\dfrac{4}{3}:\dfrac{7}{3}=\dfrac{5}{3}:\dfrac{1}{3}+\dfrac{4}{7}=5+\dfrac{4}{7}=\dfrac{39}{7}\)
Đúng 6
Bình luận (0)
cho biểu thức A = 2x(x + y) - x +7 - y
a)Tính giá trị của biểu thức A tại x = -1 và y = 3
b)Tính giá trị của biểu thức A tại x = -1 và |y| = 3
a) Thay x = -1 và y = 3 vào A, ta được :
A = 2.(-1)[(-1) + 3] - (-1) + 7 - 3
A = -2.2 + 1 + 4
A = -4 + 5
A = 1
b) |y| = 3 => \(\orbr{\begin{cases}y=3\\y=-3\end{cases}}\)
*Thay x =-1 và y = 3 vào biểu thức :
Phần này bạn sẽ làm ý như câu a vậy :33
*Thay x = -1 và y =-3 vào A, ta được :
A = 2.(-1).[(-1) + (-3)] - (-1) + 7 - (-3)
A = -2.(-4) + 1 + 7 + 3
A = 8 + 11
A = 19
1) Cho đa thức : A 2X-3XY2+1. Tính giá trị của A tại x -2 và y3.2)Cho phân thức : Bdfrac{x^2-10x+25}{x^2-25}a. Tìm điều kiện xác định của B b. Tính giá trị của B tại x -1.3)Tính : C (dfrac{9}{X^3-9X} +dfrac{1}{X+3}):(dfrac{X-3}{X^2+3X} -dfrac{X}{3X+9})4) Cho tam giác ABC vuông tại A (abac). Gọi M ,N theo thứ tự là trung điểm của AB và AC . Trên tia đối của tia NM lấy điểm D soa cho : NDNMa. C/M : tứ giác BMCD là hbhb. Tứ giác AMDC là hình j ? vì soa ?c. C/M : tam giác BDA cân MN BIẾT CÂU NÀO TH...
Đọc tiếp
1) Cho đa thức : A = 2X-3XY2+1. Tính giá trị của A tại x= -2 và y=3.
2)Cho phân thức : B=\(\dfrac{x^2-10x+25}{x^2-25}\)
a. Tìm điều kiện xác định của B
b. Tính giá trị của B tại x= -1.
3)Tính : C= (\(\dfrac{9}{X^3-9X}\) +\(\dfrac{1}{X+3}\)):(\(\dfrac{X-3}{X^2+3X}\) -\(\dfrac{X}{3X+9}\))
4) Cho tam giác ABC vuông tại A (ab<ac). Gọi M ,N theo thứ tự là trung điểm của AB và AC . Trên tia đối của tia NM lấy điểm D soa cho : ND=NM
a. C/M : tứ giác BMCD là hbh
b. Tứ giác AMDC là hình j ? vì soa ?
c. C/M : tam giác BDA cân
MN BIẾT CÂU NÀO THÌ LÀM CÂU ĐÓ CŨNG ĐƯỢC AH!
Bài 3:
\(C=\left(\dfrac{9}{x\left(x-3\right)\left(x+3\right)}+\dfrac{1}{x+3}\right):\left(\dfrac{x-3}{x\left(x+3\right)}-\dfrac{x}{3\left(x+3\right)}\right)\)
\(=\dfrac{9+x^2-3x}{x\left(x-3\right)\left(x+3\right)}:\dfrac{3x-9-x^2}{3x\left(x+3\right)}\)
\(=\dfrac{x^2-3x+9}{x\left(x-3\right)\left(x+3\right)}\cdot\dfrac{3x\left(x+3\right)}{-\left(x^2-3x+9\right)}\)
\(=\dfrac{-3}{x-3}\)
Đúng 1
Bình luận (0)
cho biểu thức A=2x(x+2y)-x+4-2y
a) tính giá trị của A tại x=-1 và y=2
b) tính giá trị của A tại x=1 và |y| =3
c)tính giá trị của A khi x=-2y
GIÚP EM VỚI , EM CẦN GẤP***
Có biểu thức \(A=2x\left(x+2y\right)-x+4-2y\)
a) Thay \(x=-1;y=2\) vào biểu thức trên, ta có :
\(A=2\left(-1\right)\left[\left(-1\right)+2.2\right]-\left(-1\right)+4-2.2\)
\(A=\left(-2\right)+3+1+4-4=\left(-2\right)+4=2\)
b) Xét 2 trường hợp của \(|y|=3:y=3;y=-3\) và thay x = 1 vào các biểu thức
Có TH1 : \(A=2.1\left(1+2.3\right)-1+4-2.1=12-1+4=15\). TH2 :
\(A=2.1\left[1+2\left(-3\right)\right]-1+4-2.\left(-3\right)=\left(-10\right)-1+4-\left(-6\right)=-1\)
c) Thay \(x=-2y\) vào biểu thức, ta có : \(A=2x\left[\left(-2y\right)+2y\right]-x+4+x\)
\(A=2x.0+\left(x-x\right)+4=0+0+4=4\)
Ôí chồi chồi chồi !
\(A=2\left(-1\right)\left[\left(-1\right)+2.2\right]....\)
''....'' lak vế sau
Cậu giỏi ghê, bên trên lak nhân DẤU nhân đấy.
Bài 3:
a) Tính giá trị của biểu thức tại P = x(x - y) + y(x - y) tại x = 5 và y = 4;
b) Tính giá trị của biểu thức tại Q = x(x2 - y) - x2(x + y) + y(x2 - x) tại x = 1/2 và y = -100;
a) \(P=x\left(x-y\right)+y\left(x-y\right)=\left(x-y\right)\left(x+y\right)=x^2-y^2=5^2-4^2=9\)
b) \(Q=x\left(x^2-y\right)-x^2\left(x+y\right)+y\left(x^2-x\right)=x^3-xy-x^3-x^2y+x^2y-xy=0\)
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
Cho phân thức 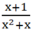
a) Tìm điều kiện của x để giá trị của phân thức được xác định.
b) Tính giá trị của phân thức tại x = 1 000 000 và tại x = - 1
a) Ta có: x2 + x = x(x + 1)
Giá trị phân thức này được xác định với điều kiện x2 + x ≠ 0
⇒ x(x + 1) ≠ 0 ⇒ x ≠ 0 và x + 1 ≠ 0
⇒ x ≠ 0 và x ≠ -1
b) Vì 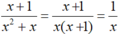 và x = 1 000 000 thỏa mãn điều kiện của biến nên có thể tính giá trị của phân thức đã cho bằng cách tính giá trị của phân thức rút gọn
và x = 1 000 000 thỏa mãn điều kiện của biến nên có thể tính giá trị của phân thức đã cho bằng cách tính giá trị của phân thức rút gọn 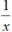
Vậy giá trị của phân thức đã cho tại x = 1 000 000 là 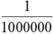
+ Tại x= -1 phân thức đã cho không được xác định.
Vậy không tồn tại giá trị của phân thức tại x = -1
Đúng 0
Bình luận (0)