Cho tam giác giác ABC vuông tại A. Gọi G là trọng tâm tâm giác ABC BiếtAb=3cm,AB=4cm.Tình hình Ag

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A. Gọi G là trọng tâm tâm giác ABC Biết AB=3cm, AC=4cm. TÍNH Ag
Hình em tự vẽ ra nhé.
Áp dụng đl pytago vào tam giác vuông ABC có:
AB^2 + AC^2 = BC^2
-- > BC = 5 (cm)
Vì tam giác ABC vuông tại A, AM là đường trung tuyến ứng với cạnh huyền BC nên ta có:
\(AM=\dfrac{1}{2}BC=\dfrac{1}{2}.5=2,5\left(cm\right)\)
Vì G là trọng tâm tâm giác ABC, ta lại có:
\(AG=\dfrac{2}{3}AM=\dfrac{2}{3}.2,5=\dfrac{5}{3}\left(cm\right)\)
Đúng 2
Bình luận (0)
Tam giác ABC cân tại A có AB=5cm; BC=8cm. Gọi G là trọng tâm của tam giác đó thì độ dài của AG sẽ là bao nhiêu?
A. AG = 1cm
B. AG = 2cm
C. AG = 3cm
D. AG = 4cm
giúp mình với ạ
Cho tam giác ABC vuông tại A có đường trung tuyến AM. Từ M kẻ vuông góc với AB tại E, vuoing góc với AC tại F. Gọi G là trọng tâm của tam giác ABC CM: ( AG + BC)÷2> BG
Cho tam giác ABC vuông tại A,AB=5;AC=12 a)Tính Bc b)gọi m là trung điểm bc tính AM c)gọi g là trọng tâm của tam giác abc.tính AG d) kẻ đường cao AH.tính diện tích tam giác ABC,tính AH
cho tam giác abc cân tại a có ab=ac=10cm bc=8cm gọi g là trọng tâm của tam giác abc tính ag,bg,cg
Xem chi tiết
Cho tam giác abc vuông tại a ab=6cm;ac=8cm. Trên ab lấy d sao cho ad=3cm. Trên tia đối của ac lấy i sao cho ac=ai
a) cm tam giác adc=tam giác adi
b) cm tam giác bci cân
c) gọi g là trọng tâm của tam giác abc . Tính gc
a: Xét ΔADC vuông tại A và ΔADI vuông tại A có
AD chung
AC=AI
=>ΔADC=ΔADI
b: Xét ΔBCI có
BA là đườg cao, là trung tuyến
=>ΔBCI cân tại B
c: \(CD=\sqrt{8^2+3^2}=\sqrt{73}\left(cm\right)\)
=>\(CG=\dfrac{2}{3}\sqrt{73}\left(cm\right)\)
Đúng 0
Bình luận (0)
Bài 2 a, Cho tam giác abc vuông tại a. AB= 4 cm, BC= 7 cm. Tính AC. b, G là trọng tâm của tam giác abc. Tính AG
Bài 2 a, Cho tam giác abc vuông tại a. AB= 4 cm, BC= 7 cm. Tính AC. b, G là trọng tâm của tam giác abc. Tính AG
a: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2+16=49\)
=>\(AC=\sqrt{49-16}=\sqrt{33}\left(cm\right)\)
b: Gọi M là trung điểm của BC
Xét ΔABC có
AM là đường trung tuyến
G là trọng tâm
Do đó: AG=2/3AM
ΔABC vuông tại A có AM là đường trung tuyến
nên \(AM=\dfrac{BC}{2}=3,5\left(cm\right)\)
=>\(AG=\dfrac{2}{3}\cdot AM=\dfrac{2}{3}\cdot\dfrac{7}{2}=\dfrac{7}{3}\left(cm\right)\)
Đúng 0
Bình luận (0)
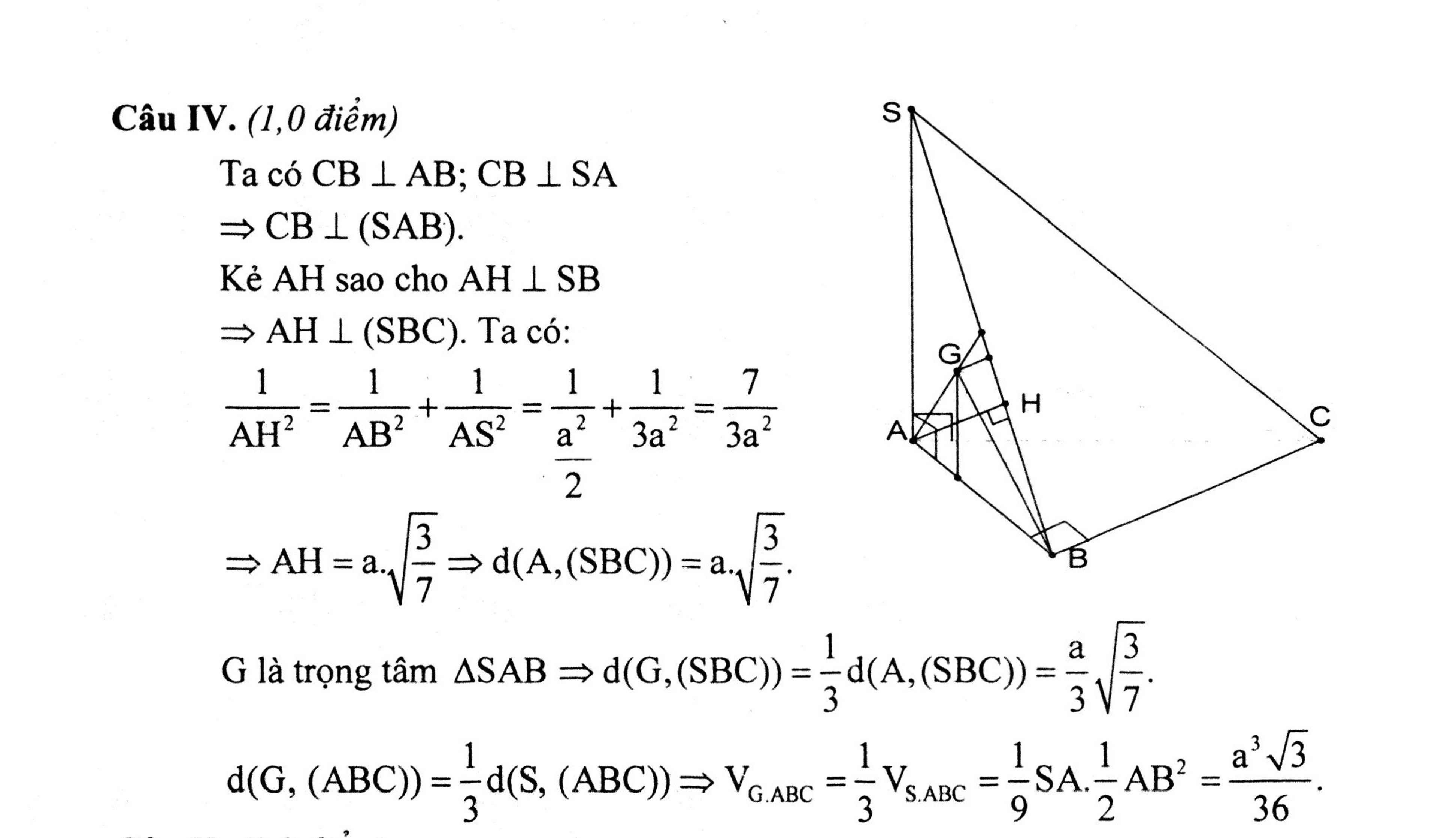
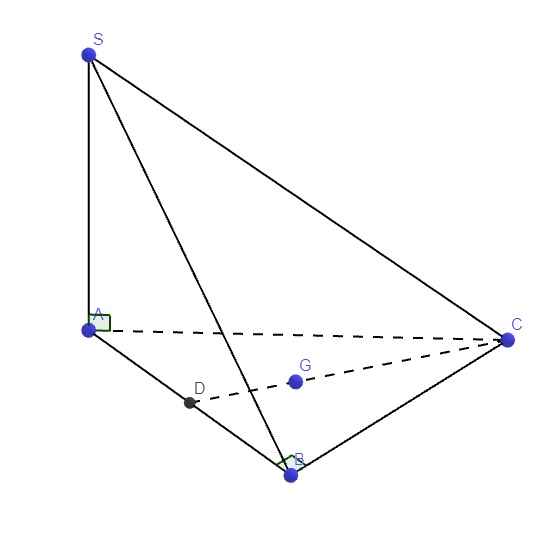
Cho hình chóp S.ABC đáy ABC là tam giác vuông cân tại B. Cạnh AB=a . SA vuônh góc với (ABC) , SA=a căn 2 Gọi G là trọng tâm tam giác ABC. Tính (G,(SAB))
Cho hình chóp S.ABC đáy ABC là tam giác vuông cân tại B. Cạnh AB=a . SA vuônh góc với (ABC) , SA=a căn 2 Gọi G là trọng tâm tam giác ABC. Tính (G,(SAB))
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC=d\left(C;\left(SAB\right)\right)\)
Gọi D là trung điểm AB, theo tính chất trọng tâm: \(GD=\dfrac{1}{3}CD\)
\(\Rightarrow d\left(G;\left(SAB\right)\right)=\dfrac{1}{3}d\left(C;\left(SAB\right)\right)=\dfrac{1}{3}BC=\dfrac{1}{3}AB=\dfrac{a}{3}\)
Đúng 3
Bình luận (0)