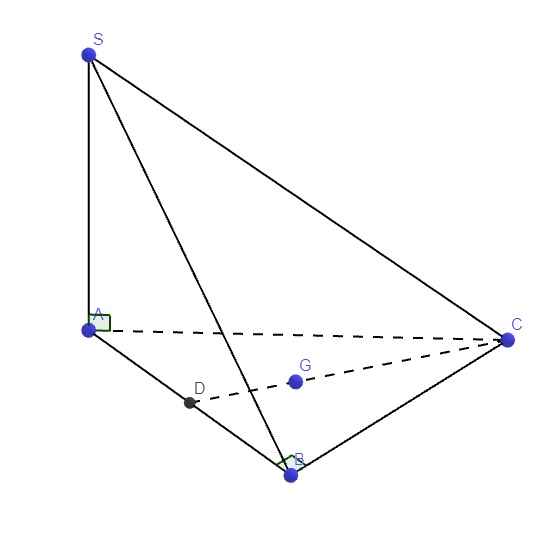
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC=d\left(C;\left(SAB\right)\right)\)
Gọi D là trung điểm AB, theo tính chất trọng tâm: \(GD=\dfrac{1}{3}CD\)
\(\Rightarrow d\left(G;\left(SAB\right)\right)=\dfrac{1}{3}d\left(C;\left(SAB\right)\right)=\dfrac{1}{3}BC=\dfrac{1}{3}AB=\dfrac{a}{3}\)