a>0 => góc nhọn

a<0 => góc tù 

Vì 2>0 nên góc tạo đc là góc nhọn

Ta có hệ số góc của đths là 2

Gọi góc cần tìm là \(\alpha< 90^0\)

\(\Rightarrow\tan\alpha=2\approx\tan63^0\\ \Rightarrow\alpha\approx63^0\)

Vậy góc tạo bởi đths và Oc xấp xỉ 63 độ

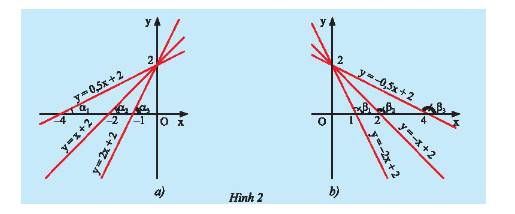
b)

- Ở hình 2a là đồ thị của 3 hàm số \(y = 0,5x + 2;y = x + 2;y = 2x + 2\).

Ta có: \({a_1} = 0,5;{a_2} = 1;{a_3} = 2\) nên \({a_1} < {a_2} < {a_3}\).

Ta có: \({\alpha _1} < {\alpha _2}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).

\({\alpha _2} < {\alpha _3}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).

Do đó, \({\alpha _1} < {\alpha _2} < {\alpha _3}\).

- Ở hình 2b là đồ thị của 3 hàm số \(y =  - 2x + 2;y =  - x + 2;y =  - 0,5x + 2\).

Ta có: \({a_1} =  - 2;{a_2} =  - 1;{a_3} =  - 0,5\) nên \({a_1} < {a_2} < {a_3}\).

Ta có: \({\beta _1} < {\beta _2}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).

\({\beta _2} < {\beta _3}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).

Do đó, \({\beta _1} < {\beta _2} < {\beta _3}\).

- Gọi phương trình đường thẳng cần tìm có dạng : y = ax + b

- Thay tọa độ của điểm O và P và hàm số ta được hệ :

\(\left\{{}\begin{matrix}0a+b=0\\a\sqrt{3}+b=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}b=0\\a=\dfrac{\sqrt{3}}{3}\end{matrix}\right.\)

=> Phương trình đường thẳng là : \(y=\dfrac{\sqrt{3}}{3}x\)

\(\Rightarrow Tan\alpha=a=\dfrac{\sqrt{3}}{3}\)

\(\Rightarrow\alpha=30^o\)

Vậy ...

a: Vì (d)//y=1/2x+1 nên \(\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b\ne1\end{matrix}\right.\)

Vậy: (d): \(y=\dfrac{1}{2}x+b\)

Thay x=2 và y=2 vào (d), ta được:

\(b+\dfrac{1}{2}\cdot2=2\)

=>b+1=2

=>b=1

vậy: (d): \(y=\dfrac{1}{2}x+1\)

b: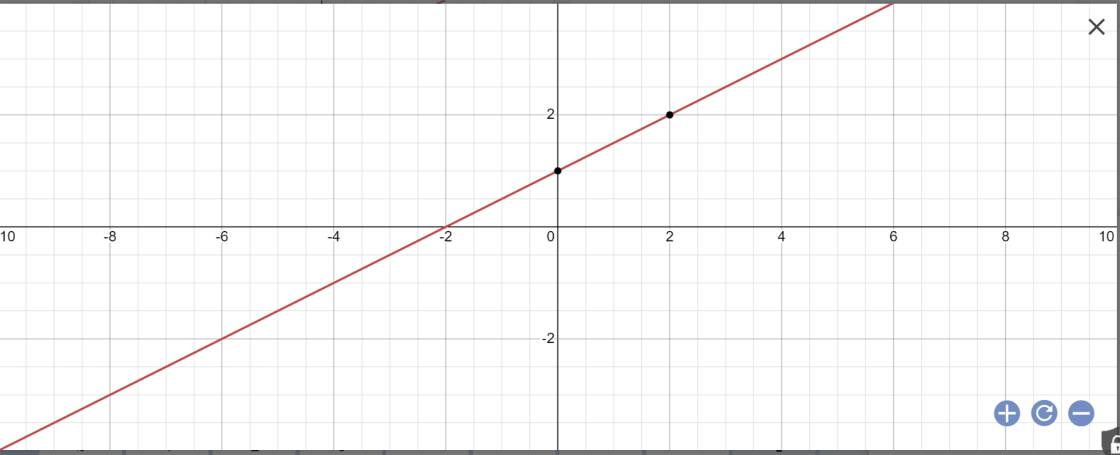 

c: Gọi \(\alpha\) là góc tạo bởi (d) với trục Ox

Ta có: (d): \(y=\dfrac{1}{2}x+1\)

=>a=1/2

=>\(tan\alpha=a=\dfrac{1}{2}\)

=>\(\alpha\simeq26^034'\)

d: tọa độ B là:

\(\left\{{}\begin{matrix}y=0\\\dfrac{1}{2}x+1=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=0\\\dfrac{1}{2}x=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-2\end{matrix}\right.\)

Tọa độ C là;

\(\left\{{}\begin{matrix}x=0\\y=\dfrac{1}{2}x+1=\dfrac{1}{2}\cdot0+1=1\end{matrix}\right.\)

Vậy: B(-2;0); C(1;0)

\(OB=\sqrt{\left(-2-0\right)^2+\left(0-0\right)^2}=\sqrt{2^2+0^2}=2\)

\(OC=\sqrt{\left(1-0\right)^2+\left(0-0\right)^2}=\sqrt{1^2+0^2}=1\)

Vì Ox\(\perp\)Oy nên OB\(\perp\)OC

=>ΔBOC vuông tại O

=>\(S_{BOC}=\dfrac{1}{2}\cdot OB\cdot OC=\dfrac{1}{2}\cdot2\cdot1=1\)

a: Thay x=1 và y=-2 vào y=ax+1, ta được:

a+1=-2

hay a=-3

Vậy: (d'): y=-3x+1

c: Tọa độ giao điểm của (d) và (d') là:

\(\left\{{}\begin{matrix}-3x+1=x+3\\y=x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=3-\dfrac{1}{2}=\dfrac{5}{2}\end{matrix}\right.\)